ББК 22.1я2я72

Г96

Домодрян Александр Петрович

Математические игры и развлечения

Избранное

Редактор Копылова А.Н.

Техн. Редактор Мурашова Н.Я.

Корректор Сечейко Л.О.


Сдано в набор 26.09.2003.Подписано к печати 14.12.2003.Формат 84*108¼

Физ. печ. л. 8,375.Условн. печ. л. 13,74. Уч - изд.л. 12,82. Тираж 200 000 экз.

Заказ№979.Цена книги 50руб.

. Доморяд А.П.

Математические игры и развлечения: Избранное.-Волгоград:ВГПУ,2003.-20с
В книге представлены избранные задачи из монографии Доморяда А.П.

«Математические игры и развлечения»,которая была издана в 1961году.

Государственным издательством физико-математической литературы г. Москвы.


ISBN5-09-001292-X ББК22.1я2я72

Издательство «ВГПУ»,2003

Определение задуманного числа по трем таблицам

Разместив в каждой из трех подряд числа от 1 до 60 так, чтобы в первой таблице они стояли в трех столбцам по двадцати чисел в каждом, во второй -в

I	II	III
1	2	3		I	II	III	IV		I	II	III	IV	V
4	5	6		1	2	3	4		1	2	3	4	5
7	8	9		5	6	7	8		6	7	8	9	10
.	.	.		.	.	.	.		.	.	.	.	.
.	.	.		.	.	.	.		.	.	.	.	.
.	.	.		.	.	.	.		.	.	.	.	.
55	56	57		53	54	55	56		51	52	53	54	55
58	59	60		57	58	59	60		56	57	58	59	60

---

Четырех столбцах по 15 чисел в каждом и в третьей - в пяти столбцах по 12 чисел в каждом (см.рис.1),легко быстро определить задуманное кем – нибудь число N(N≤60),если будут указаны номера α, β, γ столбцов, содержащих задуманное число в 1-й,во 2-йи в 3-й таблицах:N будет остатку от деления числа 40а+45В+36у на 60 или, другими словами,N будет равно меньшему положительному числу, сравнимому с суммой (40а+45В+36у)по модулю 60.Например,при а=3,В=2,у=1:

40а+45В+36у=0+30+36=6(mod60),т.е.N=6.

Рис.1

Аналогичный вопрос может быть решен для чисел в пределах до 420,размещеных в четырех таблицах с тремя, четырьмя ,пятью и семью столбцами: если α,β,γ,-номера столбцов, в которых стоит задуманное число, то оно равно остатку от деления числа 280а+105В+336у+120г на 420.

Солитер

Игра под названием солитер проводится на доске с тридцатью тремя клетками. Такую доску легко получить, прикрыв шахматную доску листом картона с крестообразным вырезом

			73	74	75
			63	64	65
	51	52	53	54	55	56	57
	41	42	43	44	45	46	47
	31	32	33	34	35	36	37
			23	24	25
			13	14	15

---

На рисунке каждая клетка обозначена парой чисел, указывающих номера горизонтально и вертикального рядов, на пересечении которых находится клетка. В начале игры все клетки, за исключением какой-нибудь одной, заняты шашками.

Требуется снять 31 шашку, причем задаются пустая «начальная» клетка (a,b) и

«конечная» (с,d), на которой должна оказаться уцелевшая в конце игры шашка. Правила игры таковы: любая шашка может быть снята с доски, если рядом с ней (в горизонтальном или вертикальном направлении) находится с одной стороны какая-нибудь шашка («снимающая»), а с противоположной стороны-пустая клетка, на которую «снимающая» шашка должна быть при этом переведена.

Из теории игры следует, что решение будет в том и только в том случае, когда а = с(mod3) и b = d (mod3).

Приведем для примера решения задачи, в которой клетка (44)является и начальной, и конечной.

1.64-44 6.75-73 11.65-45 16.34-36

2.56-54 7.43-63 12.15-35 17.37-35

3.44-64 8.73-53 13.45-25 18.25-45

4.52-54 9.54-52 14.37-35 19.46-44

5.73-53 10.35-55 15.57-37 20.23-43

21. 31-33 22. 43-23 23. 51-31

24. 52-32 27. 34-32 30. 34-54

25. 31-33 28. 13-33 31. 64-44

26. 14-34 29. 32-34

Здесь в записи каждого хода указаны для «снимающей» шашки номер исходной клетки, на которую она ставится (при этом с доски снимается шашка, стоящая на промежуточной клетке)

Попробуйте снять 31 шашку:

А) при начальной клетке (5,7)и конечной (2,4);

Б)при начальной клетке (5,5) и конечной (5,2)
Сложение и вычитание вместо умножения

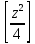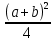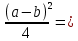
До изобретения таблиц логарифмов для облегчения уможение многозначных чисел применялись так называемые простаферетические таблицы (от греческих слов « простезис » - прибавление и « афайрезис » -отнятие),представляющие собой таблицы значений функций при натуральных значениях z. Так как при а и b целых ab= – – 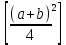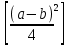( числа a+b и a-b либо оба честные, либо оба нечестные; в последнем случае дробные части у

---

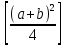и 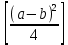, взятых из таблицы.

Для перемножения трех чисел можно воспользоваться тождеством:

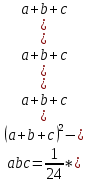
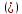
Из которого следует, что при наличии таблицы значений функции 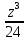вычисление произведения 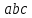можно свести к определению чисел a+b+c, a+b-c, a+c-b, b+c-a и по ним – при помощи таблицы- правой части равенства 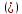. Приведем в качестве примера такую таблицу для 1 ≤ z ˂ 30. В таблице даны: крупными цифрами – значения 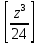а мелкими –значения k, где при 0 ≤ k ≤ 23 .

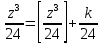					единицы
		0	1	2	3	4	5	6	7	8	9
	0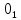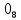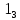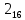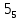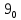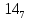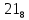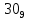
Десятки	1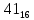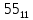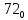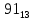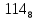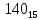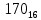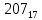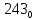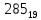
	2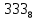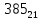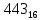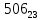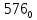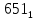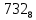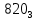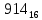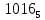

---

Нетрудно, пользуясь формулой и таблицей, получит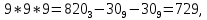
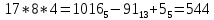(проверьте!)


Функция 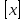(целая часть х)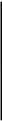



















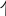
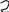
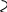
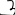
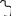
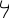
Функция

---

Смотрите также файлы

• Вариант 12 x 1 v1 X2 X3 X4 v3 v7 v10 v6 v8 v11 v4 v9 v5 v2 X5 X6 X7 v12 X8 Дать словесное описание графа.docx

• Понятие Определение или характеристика, либо окончание предложения.docx

• Контрольные вопросы по курсу " Дискретная математика".docx

• 1. Построить граф биологической классификации видов. Используя граф, определить, какими признаками будут обладать следующие существа.docx

• Реферат по культурологии Жена путешественника во времени.doc