ДӘРІСТЕР ЖИНАҒЫ
№1 дәріс

Тақырыбы: КІРІСПЕ. Материалдық нүкте механикасы.

Қаралатын мәселелер: Материалдық нүкте. Механикалық қозғалыс. Траектория, жүрілген жол, орын ауыстыру, үдеу. Материалдық нүктенің қозғалыс теңдеулері. Материалдық нүкте динамикасы. Ньютон заңдары. Кеплер заңдары. Космостық жылдамдықтар. Импульс және энергия. Консервативтік және консервативтік емес күштер. Энергия мен импульстің сақталу заңдары. Центрифуга және оның қолданылуы.
Кіріспе. Физика материяның қарапайым қозғалыстарын және осы қозғалыстарға сәйкес табиғаттың жалпы заңдарын зерттейтін ғылым. Физикалық зерттеулердің әдістері: тәжірибе, гипотеза, эксперимент, теория. Физиканың дамуының басты кезеңдері – И.Ньютон механикасынан Дж.Максвеллдің электромагниттік өріс теориясын және кванттық көзқарастардың тууына, салыстырмалы теория мен кванттық механиканы құру сол сияқты атомдық, ядролық физиканың және қазіргі физиканың әртүрлі салаларының теориялық базасын жасаудағы орны. Техниканың физиканың дамуына ықпалы. Физиканың басқа ғылымдармен байланысы.

Механика – материя қозғалысының ең қарапайым формасын, яғни денелердің немесе олардың жеке бөліктерінің бір-бірімен салыстырғанда орын ауыстыруын зерттейтін ғылым.

Механикалық қозғалыс уақыт өтуімен денелердің немесе дененің бөліктерінің кеңістікте бір-біріне қатысты орны өзгеруі.

Классикалық механика – жылдамдығы вакуумдағы жарық жылдамдығымен салыстырғанда анағұрлым аз макроскопиялық денелердің (Галилей мен Ньютон механикасы) қозғалыс заңдарын зерттейді.

Релятивистік механика – жылдамдығы вакуумдағы жарық жылдамдығымен шамалас макроскопиялық денелердің (Эйнштейн тұжырымдаған АСТ) қозғалыс заңдарын зерттейді.

Кванттық механика - микроскопиялық денелердің (жеке атомдардың мен элементар бөлшектердің) қозғалыс заңдарын зерттейді.

Табиғаттағы қозғалыстың ең қарапайым түрі – механикалық қозғалыс. Оның сан алуан түрлері болуы мүмкін. Жалпы айтқанда, механикалық қозғалыс дегеніміз бір дененің басқа материалдық денелермен салыстырғанда орын ауыстыруы. Кеңестікте қозғалыстағы денелерді қозғалмайтын басқа денелермен салыстырып қарастыратын жүйені санақ жүйесі дейді. Практикада қозғалысты сипаттау үшін санау жүйесін құрайтын денелерге бір координаттар жүйесін, мәселен, кәдімгі түзу сызықты тікбұрышты координаттар жүйесін байланыстыруға болады.

Физикалық денелердің немесе бөліктерінің қозғалысын қарастырғанда, олардың нүктесінің қозғалысын зертттеу қажет. Өйткені, материалдық нүктенің қозғалысы – кинематиканың заңдылықтарын зерттеудің негізі.

---

Сонымен материалдық нүкте дегеніміз массасы қарастырылып отырған дененің массасына тең геометриялық нүкте. Денені егер оның бөлшектері бірдей және жүрілген жолдары дененің өлшемімен салыстырғанда айтарлықтай үлкен болғанда ғана материалдық нүкте ретінде қарастыруға болады.

Қарастырылып отырған материалдық нүктенің қозғалыс кезінде із қалдыруын оның траекториясы дейді. Траекторияның формасына қарай, қозғалысты түзу сызықты және қисық сызықты деп бөледі.

Кинематика деп денелердің қозғалысын зерттейтін, бірақ қозғалыстың туу себебін қарастырмайтын физиканың бөлімі.

Механикалық қозғалыс деп уақыт өзгерісінде кеңістікте дененің басқа денелерге қатысты орын ауыстыруын айтамыз.

Механикалық қозғалыс – салыстырмалы. Бір дененің әр түрлі денелерге қатысты қозғалысы әр түрлі болады. Дененің қозғалысын сипаттау үшін, қозғалыс қай денеге қатысты қарастырылатынын белгілеу қажет. Бұл денені санақ денесі деп атайды. Санақ денесі және уақыт – санақ жүйесін құрап, ол қозғалған дененің кез келген уақыттағы орнын анықтауға мүмкіндік береді.

Халықаралық бірліктер жүйесінде (СИ) ұзындықтың бірлігі ретінде метр, ал уақыттың бірлігі ретінде – секунд қабылданған.

Әрбір дене белгілі бір өлшемдерге ие. Дененің әр түрлі бөліктері кеңістіктің әр түрлі жерлерінде орналасады. Алайда, механиканың көпшілік есептерінде дененің әр түрлі бөліктерінің орнын көрсетудің қажеті жоқ. Егер дененің өлшемдері басқа денелерге дейінгі арақашықтығынан аз болса, онда бұл денені оның материалдық нүктесі деп санауға болады. Мәселен, оны ғаламшарлардың Күннің айналасындағы қозғалысын зерттегенде алуға болады. Егер дененің барлық бөліктері бірдей қозғалса, ондай қозғалысты ілгерілемелі қозғалыс деп аталады. Мысалы үшін, «Гиганттық дөңгелек» аттракционындағы кабиналар, жолдың түзу сызықтық бөлігіндегі автомобиль және басқалар ілгерілемелі қозғалады. Дененің ілгерілемелі қозғалысында оны материалдық нүкте ретінде қарастыруға болады.

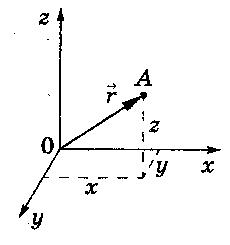
Материалдық нүктенің орны координатардың декарттық жүйесінде х, у, z координаттарымен немесе 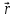– радиус вектормен (1.1-сурет) анықталады.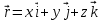

Қозғалыстағы материалдық нүктенің координаттары уақыт өтуімен өзгеріп отырады. Жалпы жағдайда, нүктенің қозғалысы x = x(t), y = y(t) және z = z(t) (1) скаляр теңдеулер жүйесімен , немесе

---

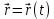
(2) радиус-векторы арқылы анықтау.

(1) және (2) теңдеулер материалдық нүкте қозғалысының кинематикалық теңдеуі д.а.

Радиус вектор уақыттың бастапқы кезіндегі нүктенің орны.

Өлшемдерін берілген жағдайда ескермеуге болатын денені материалдық нүкте деп атайды.

Материалдық нүкте ұғымы механикада маңызды орын алады. Уақыт өткенде бір нүктеден екінші нүктеге орын ауыстырғанда, дене (материалдық нүкте) дене қозғалысының траекториясы деп аталатын қандай да бір қисықты сызады.

Дененің орын ауыстыруы деп дененің бастапқы орнын оның кейінгі орнымен қосатын бағытталған кесіндіні айтады. Орын ауыстыру – векторлық шама.



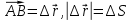
Жүрген жолы - дененің белгілі t уақыттың ішінде траектория доғасының ұзындығына тең болады. Жол – скалярлық шама. ∆S = f(t)

Жылдамдық. Қозғалыстардың бір-бірінен айырмашылығы болады, өткені әр түрлі дене бірдей уақыт аралығында түрліше жол жүруі мүмкін. Қозғалыстардың осындай өзгерісін біз жылдамдық деген ұғым енгізу арқылы сипаттаймыз. Жылдамдық деп орын

1.1 – cурет ауыстыру векторының уақыт бойынша алынған туындысына тең және траекторияға берілген нүктеде жүргізілген жанамамен бағыттас векторды айтады. Яғни дене берілген уақыт аралығында неғұрлым көп жол жүрсе, ол шама соғұрлым үлкен болады. Материалдық нүктенің радиус векторы өсімшесінің осы өзгеріс болған уақыт аралығына қатынасы орташа жылдамдық деп аталады.

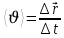(1.3)

Траекторияның берілген нүктесіндегі жылдамдық лездік жылдамдық деп аталады. Ол радиус вектордың уақыт бойынша бірінші ретті туындысына тең және қозғалыс бағытына сәйкес траекторияға жанама бойымен бағытталады:

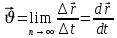(1.4)

Лездік жылдамдықтың модулі жолдың уақыт бойынша алынған бірінші туындысымен анықталады:

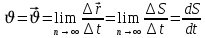(1.5)

Жылдамдықтың өлшем бірлігі м/с.

Үдеу. Бірқалыпты айнымалы қозғалыс деп кез келген өзара тең ∆t уақыт аралықтарында υ жылдамдығы бірдей ∆υ шамаға өзгеріп отыратын қозғалысты айтады. Мұнда мынадай екі жағдай болуы мүмкін: а) егер уақытқа байланысты жылдамдықтың сан мәні ұдайы артып отырса, онда қозғалыс бірқалыпты үдемелі; ә) уақытқа байланысты жылдамдықтың сан мәні ұдайы кеміп отырса, онда бірқалыпты кемімелі қозғалыс делінеді. Олай болса, уақытқа байланысты жылдамдықтың қаншалықты тез өзгеретіндігін сипаттау үшін

---

үдеу деп аталатын физикалық шама енгізіледі. Түзу сызықты бірқалыпты айнымалы қозғалыстың үдеуі (а) дегенiміз жылдамдықтың өсімшесіне тура пропорционал және осы өсімше пайда болған уақыт өсімшесіне кері пропорционал физикалық шама, яғни

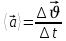(1.6)

Бұл жағдайда қозғалыс айнымалы болғандықтан жылдамдық өсімшесінің өзгеруіне сәйкес үдеу де өзгерісте болады, олай болса орташа үдеу деген ұғым ендіруге тура келеді.

Сонда 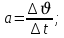немесе 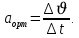(1.7)
Сонымен, берілген уақыт мезетіндегі лездік үдеу деп, орташа үдеу алынып отырған ∆t уақыт аралығы шексіз кемігенде, сол орташа үдеудің ұмтылатын шегін айтады, яғни

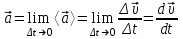(1.8)
Демек, үдеу шама жағынан жылдамдықтың уақыт бойынша алынған бірінші ретті туындысына тең болады. Ал жылдамдық υ = ds/dt болғандықтан

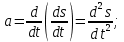(1.9)
Үдеу өлшем бірлігі м/с².

Қисық сызықты қозғалыстағы нүктенің толық үдеуі тангенциал және нормаль үдеулердің қосындысына тең. 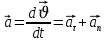(1.10)

Айналған дененің әрбір нүктесі шеңбер бойымен қозғалады да, әрқайсысының нормаль үдеуі: 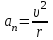; 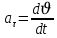(1.11)

Материалдық нүктенің t₁ - денt₂ – ге дейінгі уақыт аралығында жүрген жолын анықтау үшін υ(t) – функциясын білу керек:



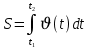
Бір қалыпты қозғалған нүктенің t - уақытта жүрген жолы:

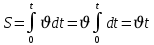(1.12)

Бір қалыпты үдемелі қозғалған нүктенің t - уақытта жүрген жолы:

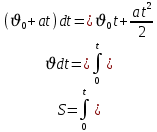(1.13)

Материалдық нүкте динамикасы. Материалдық нүктенің (дененің) массасы мен жылдамдығының көбейтіндісіне тең және бағыты жылдамдықпен сәйкес векторлық физикалық шама импульс д.а.

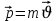(1.14)

Динамика денелердің әсерлесу кезіндегі қозғалысының өзгерісін зерттейді. Ньютонның үш заңы негізгі заңдар болып алынады. Егер қозғалысты санау жүйесіне байланыстыратын болсақ, онда қозғалушы дене әсер етуші күштен бөлек және санау жүйесімен байланысты бірқалыпты және түзу сызықты қозғалыста болады. Денеге ешқандай күш әсер етпесе, онда дене өзінің бастапқы тыныштық күйін немесе бірқалыпты түзу сызықты қозғалысын сақтайды. Материалдық денелердің мұндай қасиетін инерциялық деп атайды. Сондықтан да

---

Ньютонның бірінші заңы, инерция заңы деп аталады.

Егер денелерде инерциялық қасиет болмаса, онда оның қозғалысы үдеуді сипаттамай, тек сол уақыттағы жылдамдықтың шамасын ғана көрсетеді.

Инерциялық қасиет микроскопиялық денелер сияқты микроскопиялық денелердің бөлшектеріне де тән. Сондықтан инерция денелер қозғалысының түріне байланыссыз обьективті түрде қалыптасқан және барлық физикалық денелерге тән қасиет.

Ньютонның екінші заңы денелердің өзара әсерлесуі және ілгерлемелі қозғалысы кезінде оларда болатын өзгерістерінің байланысын сипаттайды. Сондықтан бұл заң ілгерлемелі қозғалыс динамикасының негізгі заңы бола отырып, былай тұжырымдалады:

Қозғалыс өзгерісі түсірілген күшке пропорционал және сол күшпен бағыттас болады. Ньютон қозғалыстың өзгерісін үдеудің өзгерісі деп ұқты. Олай болса, бұл заңдылық мына түрде жазылады:

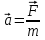(1.15)

F - денеге әсер етуші күш, m – дененің массасы, α - үдеу.

Көптеген тәжірибелердің қорытындысына сүйенсек, дененің массасы неғұрлым үлкен болса, ол соғұрлым инертті деп есептеледі, оның қозғалыс күйін өзгерту үшін көбірек күш қажет болады. Сонымен, масса дененің инерттілік мөлшері болып және оның динамикалық сипатын білдіреді. Сонда Ньютонның екінші заңын былай тұжырымдауға болады: дененің алған үдеуі әсер етуші күшке тура пропорционал, дене массасына кері пропоционал және әсер етуші күштің бағыты бойынша өзгереді.

Ньютонның екінші заңын басқа түрде де жазып көрсетуге болады. Ол үшін кинематика бөліміндегі үдеудің α = dυ / dt мәнін ескеретін болсақ, онда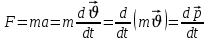

(1.16)

(1.16) - ілгерлемелі қозғалыстың динамикалық теңдеуі деп аталады. Соңғы формуланы мына түрде жазғанда 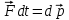, 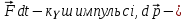дене импульсінің өсімшесі.Бұдан әсер етуші күштің импульсі дене иппульсінің өзгерісіне тең деген қорытынды жасауға болады.

Тағы бір ескеретін жай: Ньютонның екінші заңдылығындағы күшті берілген массасы m денеге әсер етуші барлық күштердің тең әсерлі күші деп түсіну керек.

R = ∑ F_i= m α , (1.17)
R = ∑ F_i= 0 . (1.18)

Сонымен, Ньютонның екінші заңынан анықталатын масса дененің инерциялық қасиетін сипаттайды. Ньютонның бүкіл әлемдік тартылыс заңымен анықталатын гравитациялық масса деген ұғым бар. Бұл масса денелердің тартылыс өрістерін қоздыру және тартылыс өзгерістерінің әсерін сезіну қабілетін сипаттайды. Дәл өлшеу кезінде инерттік масса гравитациялық массаға тең екені анықталды. Сондықтан оларды ерекше бөлудің қажеті жоқ.

---

Смотрите также файлы

• Результат попытки теста #.docx

• Сальбутамол 2 10 минута дейін созылатын тс артындаы ысып, басылатын ауырсынулар, белгілері болып табылады.docx

• Отчет о лабораторной работе 1 по общей теории связи измерение параметров детерминированных сигналов.docx

• Уголовная ответственность за экологические преступления.docx

• Отчет о лабораторной работе 2 по общей теории связи дискретизация и восстановление непрерывного сигнала.docx