Файл: Дрістер жинаЫ 1 дріс Таырыбы кіріспе. Материалды нкте механикасы. аралатын мселелер.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 261
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
консервативтік күш деп атайды. Консерватив күштің әсерінен жасалған жұмыс потенциялық энергия есебінен анықталады. Денені Жер бетінен һ1 және һ2 биіктікке көтергенде гравитациялық күштің атқаратын жұмысы потенциялық энергия деп аталады. Ол мынаған тең:
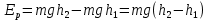 (1.35)
(1.35)
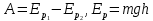
Сол сияқты консерватив күштердің қатарына серпімділік күштері де жатады. Серпімділік күшінің әсерінен жасалған жұмыс: dA=Fcepn · dx, мұндағы dx – серіппенің ұзаруы, Fcepn = - kx еске алсақ, dA= - kxdx.
Ал серіппе х1–ден х2-ге дейін созылса. онда жұмыс
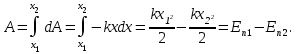 (1.36)
(1.36)
мұндағы х1 және х2 – серіппенің бастапқы және соңғы жағдайлары.
En=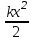 - потенциялық энергияның формуласынан көріп отырғанымыздай ол жолдың формасына байланысты емес, дененің бастапқы және соңғы орнына ғана байланысты.
- потенциялық энергияның формуласынан көріп отырғанымыздай ол жолдың формасына байланысты емес, дененің бастапқы және соңғы орнына ғана байланысты.
Энергияның сақталу заңы. Егер жүйенің күйі тек ғана консервативтік күштердің әсерінен өзгеретін болса, онда бұл күштер атқаратын жұмыс жүйенің бастапқы және соңғы орнына байланысты болады. Жүйе 1 күйден 2 күйге өткенде атқарылатын жұмыс: А1→2= En1- En2 = - (En2 – En1), мұндағы
En1, En2 – жүйенің 1 және 2 күйлердегі потенциалдық энергиялары. Соңғы формуладан көріп отырғанымыздай консерватив күштердің жұмысы потенциялық энергияның азаюына тең болады.
Элементар жұмыс үшін dA = - dEn.
Егер тұйық жүйеде тек ғана консерватив күштер әсер ететін болса, онда істелінетін элементар жұмыс мынаған тең болады: dA = dEk = - dEn, бұдан
dEk + dEn = d (Ek + En)= 0 немесе E = Ek + En = const. (1.37)
Кинетикалық және потенциялық энергияның қосындысы тұрақты шама болады. Бұл механикалық энергияның сақталу заңы болып табылады.
Центрифуга. Центрифуганың жұмысын түсіну үшін пробирканы айналу осімен айналдырғанда центрден тепкіш күштің әсерінен пробирка горизонталь орналасады. Бұрыштық жылдамдығы 60000 айн/мин тең болатын роторларда үдеу 104-105g-ге дейін жетеді. Осы центрге тартқыш күштің әсерінен пробиркадағы тығыздығы әр түрлі суспензиялар компоненттерге жіктеледі.
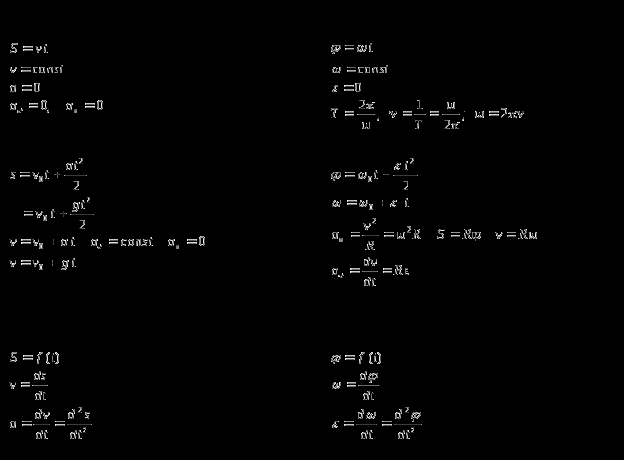
Қайталау сұрақтары
1. Материалдық нүкте, санақ жүйесі дегенді қалай түсінесің?
2. Қозғалысты сипаттайтын физикалық шамалар және олардың арасындағы байланыс.
3. Қозғалыс түрлері және олардың формулалары.
4. Жылдамдық түрлерін ата? формулаларын жаз. Күнделікті өмірде қандай жылдамдықтарды пайдаланасың?
5. Ньютон заңдарын айтып, оның ғылымда қолданылуын түсіндір.
6. Импульс пен энергияның сақталу заңдарын ғылыми тұрғыдан түсіндір.
7. Консервативтік күштер дегеніміз қандай күштер? Олардың ерекшелігін түсіндір.
№2 дәріс
Тақырыбы: Қатты дене механикасы.
Қаралатын мәселелер: Айналмалы қозғалыс түсінігі және осы қозғалысты сипаттау үшін қолданылатын физикалық шамалар. Масса орталығы, инерция моменті және күш моменті. Қатты дене динамикасының қозғалысының негізгі теңдеуі. Айналмалы қозғалыстың кинетикалық энергиясы. Гюйгенс-Штейнер теоремасы. Пішіндері әр түрлі қатты денелердің инерция моменттерін есептеу.
Қатты денелер қозғалысын қарастырғанда абсолют қатты дене ұғымын ендіріп, оны түсірілген күштер әсерінен мүлде деформацияланбайтын жорамал дене деп ұғу керек. Қатты дененің жазықтықтағы қозғалысын екі қарапайым ілгерлемелі және айнымалы қозғалыстың қосындысы деп қарастыруға болады.
Қатты денеде ойша жүргізілген түзудің өзіне-өзі паралель орын ауыстыруын ілгерлемелі қозғалыс деп түсіну керек. Айнымалы қозғалыс дегеніміз қозғалыс кезінде дененің барлық нүктелері шеңбер сызатын және олардың центрлері айналу осі деп аталатын бір түзудің бойында жататын қозғалыс.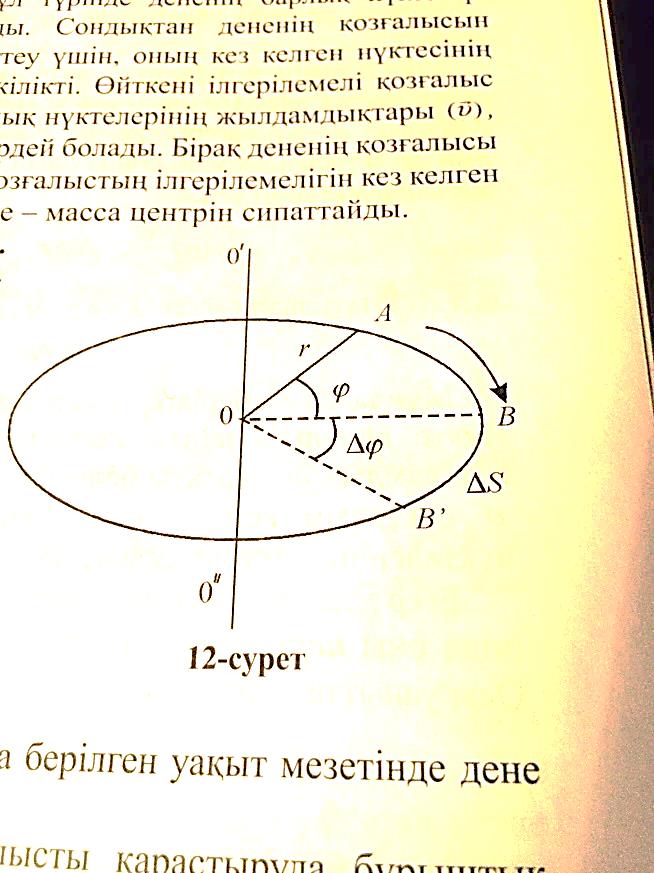
2.1-сурет Бір қалыпты айналатын дененің бұрыштық жылдамдығы деп кез келген тең уақыт аралығында бұрылатын дененің бұрылу бұрышына тура пропорционал болатын физикалық шаманы айтамыз (2.1-сурет), яғни
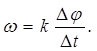 (2.1)
(2.1)
Егер k = 1 десек, онда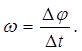
Мұндағы бұрылу бұрышы Δφ радианмен, уақыт Δt секундпен өлшенуіне байланысты бұрыштық жылдамдық рад/сек – пен өлшенеді.
Дененің бұрыштық жылдамдығы мен сызықтық жылдамдығының арасында мынадай қатыс бар.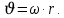 Мұндағы r – берілген нүктенің айналыс осінен қашықтығы. Егер дене Δt уақыт ішінде толық бір айналып шығатын болса, онда Δt- ны период деп атайды да, оны T – мен белгілейді. Δt = Т. Осы уақытта φ бұрышы 2π – ге артады, яғни Δφ = 2π, сонда
Мұндағы r – берілген нүктенің айналыс осінен қашықтығы. Егер дене Δt уақыт ішінде толық бір айналып шығатын болса, онда Δt- ны период деп атайды да, оны T – мен белгілейді. Δt = Т. Осы уақытта φ бұрышы 2π – ге артады, яғни Δφ = 2π, сонда
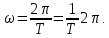
Уақыт бірлігі ішінде болатын айналыс саны n десек, онда бір период ішіндегі айналыс саны мынаған тең болады: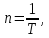 сонда
сонда 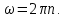
Айналған дененің әрбір нүктесі шеңбер бойымен қозғалады да, әрқайсысының нормаль үдеуі: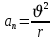 ; немесе
; немесе 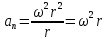 . (2.2)
. (2.2)
Бірлік уақыт ішінде бұрыштық жылдамдықтың өзгерісін сипаттайтын шаманы бұрыштық үдеу деп атайды, оны математикалық түрде былай жазады: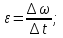 (2.3)
(2.3)
Айналыс бірқалыпты болмаған кезде бұрыштық үдеу былай табылады:
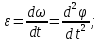 (2.3´)
(2.3´)
яғни, айналмалы қозғалыстың бұрыштық үдеуі уақыт бойынша алынған бұрылу бұрышының екінші ретті туындысына тең болады.
Егер дененің қозғалысы ілгерлемелі емес едәуір күрделі қозғалыс болса, онда дененің әр түрлі нүктелерінің жылдамдықтары мен үдеулері түрліше болады. Сыртқы күш дененің центрі арқылы өтетін сызық бойымен әсер етсе, онда оның қозғалыс мөлшері мына түрде көрсетіледі:
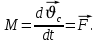 (2.4)
(2.4)
Мұндағы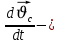 дененің массалар центрінің үдеуі.
дененің массалар центрінің үдеуі.
Сыртқы әсер болмағанда материалдық нүкте бір қалыпты түзу сызықты қозғалатын немесе тыныштық күйде болатын санақ жүйесін инерциялық деп атайды. Дененің тыныштық күйін немесе бірқалыпты түзу сызықты қозғалысын сақтауға тырысатын қасиеті инерттілік, ал сақтау құбылысы инерция деп аталады.
Масса инерттіліктің сандық өлшеуіші. Ол ілгерлемелі қозғалыстағы дененің инерттілігін сипаттайтын шама. Өзара әсерлескен екі дененің қайсысы аз үдеу алса, яғни инертті болса, соның массасы үлкен болады.
Классикалық механикада дененің массасы оның жылдамдығына тәуелді емес, дененің массасы сол денені құрайтын материалдық нүктелердің массаларының қосындысына тең, яғни масса аддитивтік қасиетке ие, толық оңашаланған денелер жүйесінде болып жатқан кез келген процесс кезінде масса өзгермейді (массаның сақталу заңы).
m = m1+m2+m3+…+mn (2.5)
Денеге басқа денелер немесе өрістердің механикалық әсер етудің өлшемін көрсететін физикалық шама
күш деп аталады. Күш– векторлық шама. Ол шамасымен, бағытымен және түсу нүктесімен сипатталады. Сонымен қатар, дененің жылдамдығын өзгертеді, яғни үдеу туғызады немесе денені деформацияға ұшыратады.
Абсолют қатты денеге әсер етуші күштің түсу нүктесін осы дененің аумағында әсер сызығы бойымен ауыстырғанда күш әсері өзгермейді. Дененің жағдайына және қозғалысына ешқандай шектеу қойылмаса, оны еркін дене деп атайды.
Инерция моментi. Күш моментi. Қатты дененің айналысын динамика тұрғысынан қарастыру кезінде күш ұғымына қоса күш моменті және масса ұғымына қоса инерция моменті деген ұғым енгізіледі. Күш моменті мына формуламен анықталады:
М = Fr ·cos α , мұндағы r ·cos α = ℓ күш иіні деп аталады. Күш моменті күш пен күш иінінің көбейтіндісіне тең. Ал инерция моменті:
І = m r2 ; (2.6)
Күш моменті мен инерция моментін пайдаланып, мынаны жазамыз:
М = I · ε; (2.7)
ε – бұрыштық үдеу, векторлық шама.
Импульс моментi және оның сақталу заңы. Симметрияның үшінші қасиеті кеңістіктің изотропты қасиеті деп аталады, яғни бұру арқылы алынған симметрия. Бұған импульс моментінің сақталу заңы дәлме-дәл келеді. Айналмалы қозғалыстың негізгі теңдеуі
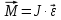 болатынын білеміз. Осы формуланы түрлендірсек:
болатынын білеміз. Осы формуланы түрлендірсек:
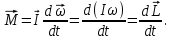 (2.8)
(2.8)
Тұйық жүйеде сыртқы күштер моменті нольге тең болса (M=0), cонда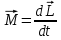 жоғарғы формула былай түрленеді.
жоғарғы формула былай түрленеді.
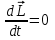 немесе
немесе 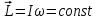 . (2.9)
. (2.9)
Яғни механикалық тұйық жүйенің импульс моменті тұрақты болады. Бұл импульс моментінің сақталу заңы деп аталады.
Симметрияның төртінші қасиеті қозғалыстағы санақ жүйесіне, басқаша айтқанда, Галилей түрлендіруіне (релятивистік емес жылдамдық) және Лоренц түрлендіруіне (релятивистік жылдамдық) қатысты симметрия. Бұл энергияның сақталу заңына сәйкес. Бұл заң тек оқшауланған жүйелерде ғана орындалады.
Біреуі массалар центрі арқылы өтетін өзара параллель oсьтерге қатысты дененің инерция моменттерінің арасындағы тәуелділікті Гюйгенс-Штейнер теоремасы береді: дененің кез келген оське қатысты инерция моменті берілген оське параллель оның массалар центрі арқылы өтетін оське қатысты инерция моменті мен дене массасының осьтер арасындағы қашықтық квадратына көбейтіндісінің қосындысына тең (дәлелдеусіз).
Сонымен, Гюйгенс-Штейнер теоремасы былай жазылады: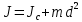
Дененің айналу О осі массалар центрі арқылы өтетін оське паралель етіп, d - қашықтықта болған жағдайда ол дененің инерция моменті.
Пішіндері әр түрлі қатты денелердің инерция моменттерін есептеу
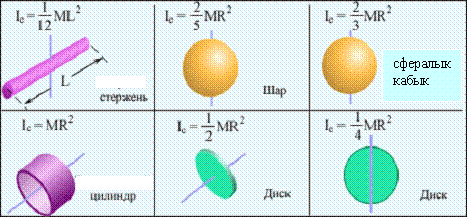
Материялық нүктенiң айналу осiне қатысты инерция моментi:
.
Айналмалы қозғалыстағы дененiң кинетикалық энергиясы:
.
Айналмалы қозғалыс кезiнде қатты дененiң кинетикалық энергиясы- оның инерция моментi мен бұрыштық жылдамдығының квадратының көбейтiндiсiнiң жартысына тең.
Жазық қозғалыстағы дененiң кинетикалық энергиясы- дененiң iлгерiлемелi және айналмалы қозғалыс кезiндегi кинетикалық энергияларының қосындысына тең болады.
.
Қайталау сұрақтары
№3 дәріс
Тақырыбы: Гидродинамика бастамалары.
Қаралатын мәселелер: Идеал сұйықтық, стационар, ламинарлық және турбулентті ағындар. Рейнольде саны. Сұйықтың ішкі үйкелісі мен тұтқырлығы. Стокс ережесі. Ағынның үздіксіздік теңдеуі. Бернулли заңы. Пуазейль формуласы. Түтікшенің ішіндегі сұйықтың қозғалысы. Жүректің қуаты және механикалық жұмысы. Ортаның кедергі күші.
Тұтас орта механикасы. Қатты дене мен газдардың аралығында өзінің қасиетіне қарай орын алатын заттың агрегаттық күйі сұйық деп аталатынын білеміз.
Газдар мен сұйықтардың тепе-теңдiгiн және қозғалысын зерттегенде оларды үздiксiз тұтас орта түрiнде қарастырады.
Сұйықтардың тепе-теңдiгiн қарастыратын механиканың бөлiмiн – гидростатика деп атайды.Сұйықтар мен газдардың серпiмдi қасиетi мынадан байқалады: олардың жеке бөлiктерi бiр-бiрiне немесе олармен жанасатын денеге сұйық пен газдардың сығылу дәрежесiне тәуелдi болатын күшпен әсер етедi. Мұндай әсер қысыммен сипатталады. Сөйтiп, сұйықтар мен газдарды сипаттайтын ең негiзгi шамалардың бiрi - қысым.
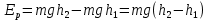 (1.35)
(1.35)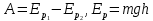
Сол сияқты консерватив күштердің қатарына серпімділік күштері де жатады. Серпімділік күшінің әсерінен жасалған жұмыс: dA=Fcepn · dx, мұндағы dx – серіппенің ұзаруы, Fcepn = - kx еске алсақ, dA= - kxdx.
Ал серіппе х1–ден х2-ге дейін созылса. онда жұмыс
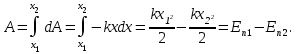 (1.36)
(1.36)мұндағы х1 және х2 – серіппенің бастапқы және соңғы жағдайлары.
En=
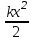 - потенциялық энергияның формуласынан көріп отырғанымыздай ол жолдың формасына байланысты емес, дененің бастапқы және соңғы орнына ғана байланысты.
- потенциялық энергияның формуласынан көріп отырғанымыздай ол жолдың формасына байланысты емес, дененің бастапқы және соңғы орнына ғана байланысты. Энергияның сақталу заңы. Егер жүйенің күйі тек ғана консервативтік күштердің әсерінен өзгеретін болса, онда бұл күштер атқаратын жұмыс жүйенің бастапқы және соңғы орнына байланысты болады. Жүйе 1 күйден 2 күйге өткенде атқарылатын жұмыс: А1→2= En1- En2 = - (En2 – En1), мұндағы
En1, En2 – жүйенің 1 және 2 күйлердегі потенциалдық энергиялары. Соңғы формуладан көріп отырғанымыздай консерватив күштердің жұмысы потенциялық энергияның азаюына тең болады.
Элементар жұмыс үшін dA = - dEn.
Егер тұйық жүйеде тек ғана консерватив күштер әсер ететін болса, онда істелінетін элементар жұмыс мынаған тең болады: dA = dEk = - dEn, бұдан
dEk + dEn = d (Ek + En)= 0 немесе E = Ek + En = const. (1.37)
Кинетикалық және потенциялық энергияның қосындысы тұрақты шама болады. Бұл механикалық энергияның сақталу заңы болып табылады.
Центрифуга. Центрифуганың жұмысын түсіну үшін пробирканы айналу осімен айналдырғанда центрден тепкіш күштің әсерінен пробирка горизонталь орналасады. Бұрыштық жылдамдығы 60000 айн/мин тең болатын роторларда үдеу 104-105g-ге дейін жетеді. Осы центрге тартқыш күштің әсерінен пробиркадағы тығыздығы әр түрлі суспензиялар компоненттерге жіктеледі.
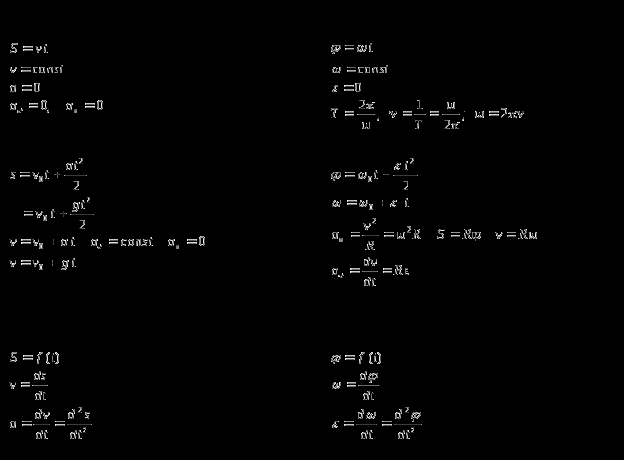
Қайталау сұрақтары
1. Материалдық нүкте, санақ жүйесі дегенді қалай түсінесің?
2. Қозғалысты сипаттайтын физикалық шамалар және олардың арасындағы байланыс.
3. Қозғалыс түрлері және олардың формулалары.
4. Жылдамдық түрлерін ата? формулаларын жаз. Күнделікті өмірде қандай жылдамдықтарды пайдаланасың?
5. Ньютон заңдарын айтып, оның ғылымда қолданылуын түсіндір.
6. Импульс пен энергияның сақталу заңдарын ғылыми тұрғыдан түсіндір.
7. Консервативтік күштер дегеніміз қандай күштер? Олардың ерекшелігін түсіндір.
№2 дәріс
Тақырыбы: Қатты дене механикасы.
Қаралатын мәселелер: Айналмалы қозғалыс түсінігі және осы қозғалысты сипаттау үшін қолданылатын физикалық шамалар. Масса орталығы, инерция моменті және күш моменті. Қатты дене динамикасының қозғалысының негізгі теңдеуі. Айналмалы қозғалыстың кинетикалық энергиясы. Гюйгенс-Штейнер теоремасы. Пішіндері әр түрлі қатты денелердің инерция моменттерін есептеу.
Қатты денелер қозғалысын қарастырғанда абсолют қатты дене ұғымын ендіріп, оны түсірілген күштер әсерінен мүлде деформацияланбайтын жорамал дене деп ұғу керек. Қатты дененің жазықтықтағы қозғалысын екі қарапайым ілгерлемелі және айнымалы қозғалыстың қосындысы деп қарастыруға болады.
Қатты денеде ойша жүргізілген түзудің өзіне-өзі паралель орын ауыстыруын ілгерлемелі қозғалыс деп түсіну керек. Айнымалы қозғалыс дегеніміз қозғалыс кезінде дененің барлық нүктелері шеңбер сызатын және олардың центрлері айналу осі деп аталатын бір түзудің бойында жататын қозғалыс.

2.1-сурет Бір қалыпты айналатын дененің бұрыштық жылдамдығы деп кез келген тең уақыт аралығында бұрылатын дененің бұрылу бұрышына тура пропорционал болатын физикалық шаманы айтамыз (2.1-сурет), яғни
Егер k = 1 десек, онда
Мұндағы бұрылу бұрышы Δφ радианмен, уақыт Δt секундпен өлшенуіне байланысты бұрыштық жылдамдық рад/сек – пен өлшенеді.
Дененің бұрыштық жылдамдығы мен сызықтық жылдамдығының арасында мынадай қатыс бар.
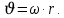 Мұндағы r – берілген нүктенің айналыс осінен қашықтығы. Егер дене Δt уақыт ішінде толық бір айналып шығатын болса, онда Δt- ны период деп атайды да, оны T – мен белгілейді. Δt = Т. Осы уақытта φ бұрышы 2π – ге артады, яғни Δφ = 2π, сонда
Мұндағы r – берілген нүктенің айналыс осінен қашықтығы. Егер дене Δt уақыт ішінде толық бір айналып шығатын болса, онда Δt- ны период деп атайды да, оны T – мен белгілейді. Δt = Т. Осы уақытта φ бұрышы 2π – ге артады, яғни Δφ = 2π, сонда
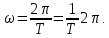
Уақыт бірлігі ішінде болатын айналыс саны n десек, онда бір период ішіндегі айналыс саны мынаған тең болады:
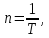 сонда
сонда 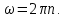
Айналған дененің әрбір нүктесі шеңбер бойымен қозғалады да, әрқайсысының нормаль үдеуі:
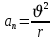 ; немесе
; немесе 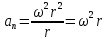 . (2.2)
. (2.2)Бірлік уақыт ішінде бұрыштық жылдамдықтың өзгерісін сипаттайтын шаманы бұрыштық үдеу деп атайды, оны математикалық түрде былай жазады:
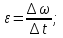 (2.3)
(2.3)Айналыс бірқалыпты болмаған кезде бұрыштық үдеу былай табылады:
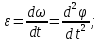 (2.3´)
(2.3´)яғни, айналмалы қозғалыстың бұрыштық үдеуі уақыт бойынша алынған бұрылу бұрышының екінші ретті туындысына тең болады.
Егер дененің қозғалысы ілгерлемелі емес едәуір күрделі қозғалыс болса, онда дененің әр түрлі нүктелерінің жылдамдықтары мен үдеулері түрліше болады. Сыртқы күш дененің центрі арқылы өтетін сызық бойымен әсер етсе, онда оның қозғалыс мөлшері мына түрде көрсетіледі:
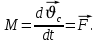 (2.4)
(2.4)Мұндағы
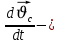 дененің массалар центрінің үдеуі.
дененің массалар центрінің үдеуі.Сыртқы әсер болмағанда материалдық нүкте бір қалыпты түзу сызықты қозғалатын немесе тыныштық күйде болатын санақ жүйесін инерциялық деп атайды. Дененің тыныштық күйін немесе бірқалыпты түзу сызықты қозғалысын сақтауға тырысатын қасиеті инерттілік, ал сақтау құбылысы инерция деп аталады.
Масса инерттіліктің сандық өлшеуіші. Ол ілгерлемелі қозғалыстағы дененің инерттілігін сипаттайтын шама. Өзара әсерлескен екі дененің қайсысы аз үдеу алса, яғни инертті болса, соның массасы үлкен болады.
Классикалық механикада дененің массасы оның жылдамдығына тәуелді емес, дененің массасы сол денені құрайтын материалдық нүктелердің массаларының қосындысына тең, яғни масса аддитивтік қасиетке ие, толық оңашаланған денелер жүйесінде болып жатқан кез келген процесс кезінде масса өзгермейді (массаның сақталу заңы).
m = m1+m2+m3+…+mn (2.5)
Денеге басқа денелер немесе өрістердің механикалық әсер етудің өлшемін көрсететін физикалық шама
күш деп аталады. Күш– векторлық шама. Ол шамасымен, бағытымен және түсу нүктесімен сипатталады. Сонымен қатар, дененің жылдамдығын өзгертеді, яғни үдеу туғызады немесе денені деформацияға ұшыратады.
Абсолют қатты денеге әсер етуші күштің түсу нүктесін осы дененің аумағында әсер сызығы бойымен ауыстырғанда күш әсері өзгермейді. Дененің жағдайына және қозғалысына ешқандай шектеу қойылмаса, оны еркін дене деп атайды.
Инерция моментi. Күш моментi. Қатты дененің айналысын динамика тұрғысынан қарастыру кезінде күш ұғымына қоса күш моменті және масса ұғымына қоса инерция моменті деген ұғым енгізіледі. Күш моменті мына формуламен анықталады:
М = Fr ·cos α , мұндағы r ·cos α = ℓ күш иіні деп аталады. Күш моменті күш пен күш иінінің көбейтіндісіне тең. Ал инерция моменті:
І = m r2 ; (2.6)
Күш моменті мен инерция моментін пайдаланып, мынаны жазамыз:
М = I · ε; (2.7)
ε – бұрыштық үдеу, векторлық шама.
Импульс моментi және оның сақталу заңы. Симметрияның үшінші қасиеті кеңістіктің изотропты қасиеті деп аталады, яғни бұру арқылы алынған симметрия. Бұған импульс моментінің сақталу заңы дәлме-дәл келеді. Айналмалы қозғалыстың негізгі теңдеуі
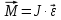 болатынын білеміз. Осы формуланы түрлендірсек:
болатынын білеміз. Осы формуланы түрлендірсек: 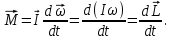 (2.8)
(2.8)Тұйық жүйеде сыртқы күштер моменті нольге тең болса (M=0), cонда
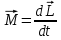 жоғарғы формула былай түрленеді.
жоғарғы формула былай түрленеді. 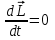 немесе
немесе 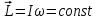 . (2.9)
. (2.9)Яғни механикалық тұйық жүйенің импульс моменті тұрақты болады. Бұл импульс моментінің сақталу заңы деп аталады.
Симметрияның төртінші қасиеті қозғалыстағы санақ жүйесіне, басқаша айтқанда, Галилей түрлендіруіне (релятивистік емес жылдамдық) және Лоренц түрлендіруіне (релятивистік жылдамдық) қатысты симметрия. Бұл энергияның сақталу заңына сәйкес. Бұл заң тек оқшауланған жүйелерде ғана орындалады.
Біреуі массалар центрі арқылы өтетін өзара параллель oсьтерге қатысты дененің инерция моменттерінің арасындағы тәуелділікті Гюйгенс-Штейнер теоремасы береді: дененің кез келген оське қатысты инерция моменті берілген оське параллель оның массалар центрі арқылы өтетін оське қатысты инерция моменті мен дене массасының осьтер арасындағы қашықтық квадратына көбейтіндісінің қосындысына тең (дәлелдеусіз).
Сонымен, Гюйгенс-Штейнер теоремасы былай жазылады:
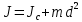
Дененің айналу О осі массалар центрі арқылы өтетін оське паралель етіп, d - қашықтықта болған жағдайда ол дененің инерция моменті.
Пішіндері әр түрлі қатты денелердің инерция моменттерін есептеу

Материялық нүктенiң айналу осiне қатысты инерция моментi:
.
Айналмалы қозғалыстағы дененiң кинетикалық энергиясы:
.
Айналмалы қозғалыс кезiнде қатты дененiң кинетикалық энергиясы- оның инерция моментi мен бұрыштық жылдамдығының квадратының көбейтiндiсiнiң жартысына тең.
Жазық қозғалыстағы дененiң кинетикалық энергиясы- дененiң iлгерiлемелi және айналмалы қозғалыс кезiндегi кинетикалық энергияларының қосындысына тең болады.
.
Қайталау сұрақтары
-
Инерция моменті дегеніміз не? Күш моменті деген не? -
Қатты дененің айналмалы қозғалысының негізгі теңдеуін жаз. -
Қатты дененің айналмалы қозғалысын қандай параметрлер арқылы сипатталады? -
Айналған қатты дененің кинетикалық энергиясы қандай шамаларға тәуелді? -
Қатты дененің серпімді деформацияларын қалай түсіндірер едің?
№3 дәріс
Тақырыбы: Гидродинамика бастамалары.
Қаралатын мәселелер: Идеал сұйықтық, стационар, ламинарлық және турбулентті ағындар. Рейнольде саны. Сұйықтың ішкі үйкелісі мен тұтқырлығы. Стокс ережесі. Ағынның үздіксіздік теңдеуі. Бернулли заңы. Пуазейль формуласы. Түтікшенің ішіндегі сұйықтың қозғалысы. Жүректің қуаты және механикалық жұмысы. Ортаның кедергі күші.
Тұтас орта механикасы. Қатты дене мен газдардың аралығында өзінің қасиетіне қарай орын алатын заттың агрегаттық күйі сұйық деп аталатынын білеміз.
Газдар мен сұйықтардың тепе-теңдiгiн және қозғалысын зерттегенде оларды үздiксiз тұтас орта түрiнде қарастырады.
Сұйықтардың тепе-теңдiгiн қарастыратын механиканың бөлiмiн – гидростатика деп атайды.Сұйықтар мен газдардың серпiмдi қасиетi мынадан байқалады: олардың жеке бөлiктерi бiр-бiрiне немесе олармен жанасатын денеге сұйық пен газдардың сығылу дәрежесiне тәуелдi болатын күшпен әсер етедi. Мұндай әсер қысыммен сипатталады. Сөйтiп, сұйықтар мен газдарды сипаттайтын ең негiзгi шамалардың бiрi - қысым.