Файл: Уральский государственный университет путей сообщения.docx

Федеральное агентство железнодорожного транспорта

Федеральное бюджетное образовательное учреждение высшего образования

Уральский государственный университет путей сообщения

Факультет ЭТФ

Кафедра Информационные технологии и защита

информации

Направление

подготовки 09.03.02 Информационные системы и технологии

Отчёт по расчетно-графической работе

По дисциплине «Геоинформационные системы»

Разработал студент

группы ИТ-318 (подпись) (дата сдачи) Петров Д.И.

Проверил

Доцент кафедры (подпись) (дата проверки) Шинкарюк В.А.

Екатеринбург

2021

Содержание

Введение

В данной расчетно-графической работе нам предстоит изучить некоторые термины и понятия из дисциплины «Инженерная геодезия» и понять их. Рассчитать дирекционные углы по уже имеющимися данными и по заданным формулам. Построить теодолитный ход по полученным значениям и начертить сам чертеж (план).

1. Исходные данные

Для вычисления координат точек съемочного обоснования в принятой на объекте системе координат выполнена привязка хода к пунктам геодезической опорной сети – исходными пунктами ПП-11, ПП-12, ПП-13.

Вариант выбирается в соответствии с последними цифрами номера в журнале и фамилии студента.

Общие данные:

• 
  ПП-11 (исходный пункт) - x₁₁=1000,00 м y₁₁=2200,00 м
  
• 
  Примычные углы – β₁^пр= 104°47,7’ β₂^пр= 62°24,0’
  

Данные в соответствии с номером в журнале:

• 
  ПП-12 x₁₂=1255,16 y₁₂=2006,88
  
• 
  ПП-13 x₁₃=1353,50 y₁₃=2232,54
  

2. Дирекционный угол

Ход начинается от исходного пункта ПП-11 (начальный ход теодолитного хода). Для начала построения вычислим значение дирекционного угла начальной стороны хода α

---

_11-2.





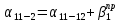
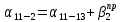
Важно заметить, что расхождение между двумя этими значениями не должно превышать 2 минут.

Для начала необходимо вычислить дирекционные углы 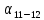и :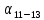




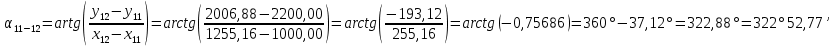
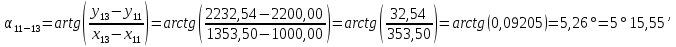
Теперь подставим наши значения в формулы для угла :







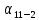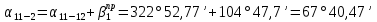
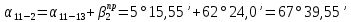
Для большей точности возьмем среднее значение:



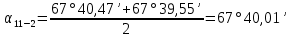
После проведенных вычислений в AutoCAD произведем построение схемы плановой привязки (рис 1.)
Схема плановой привязки:

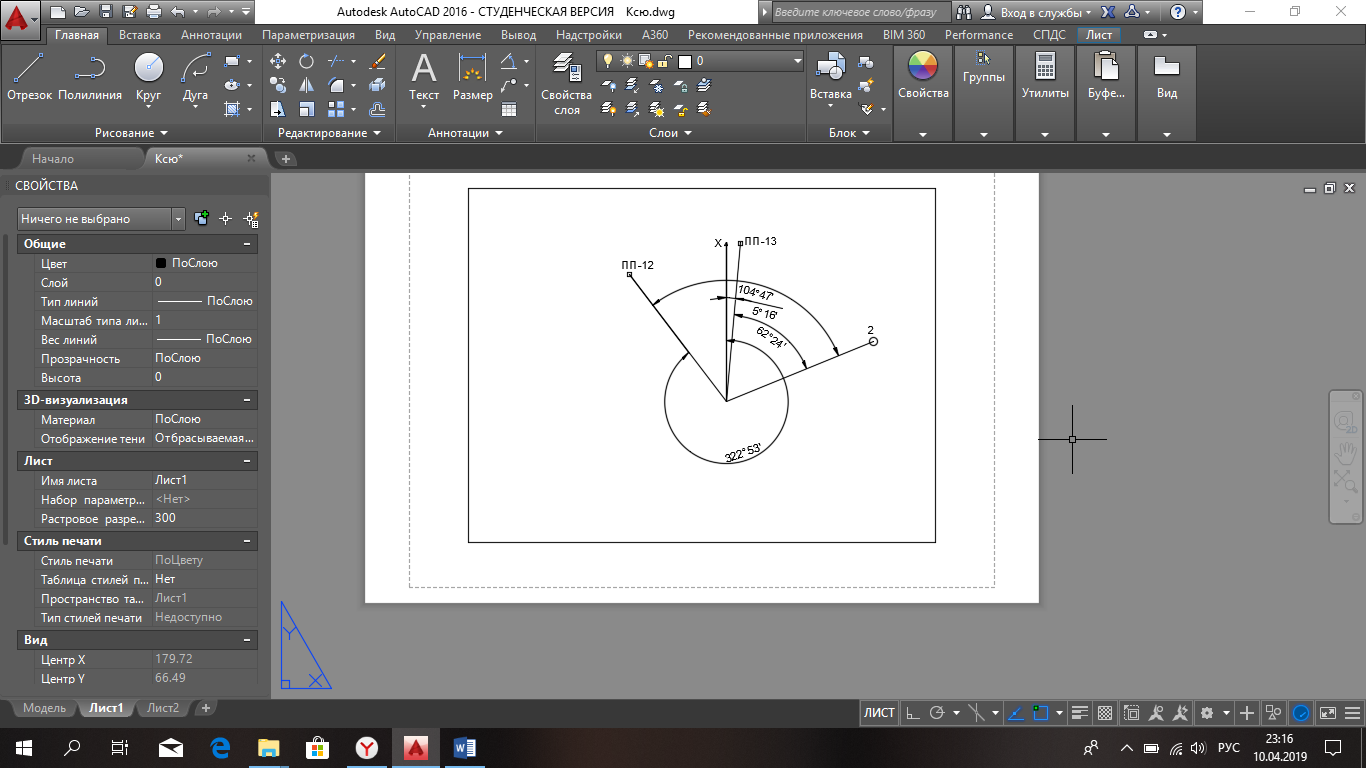
При правильном решении во всех вариантах работы минуты в среднем значении дирекционного угла начальной стороны должны получиться равными 10 или 40

Все вычисления заносятся в таблицу 1.

Таблица №1.

Вычисление координат точек точечного обоснования

№ точек	Горизонтальные углы (правые)		Дирекци-онные углы	Горизон-тальные проло-жения, м	Приращения координат, м				Координаты, м		№ точек
	Измерен. Уравнен.				Вычисленные	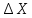	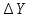Уравненные	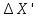	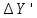X	Y
1	2	3	4	5	6	7	8	9	10	11		12
ПП-11			67°40,01’ 148°2,71’	204,42 226,09	-6 77,68 -6 -191,83	+6 189,08 +6 119,66	77,62 -191,89	189,14 119,72	1000,00	2200,00		ПП-11
2	+0,3 99°37,0’	99°37,3’							1077,62	2389,14		2
3	+0,3 92°56,5’	92°56,8’							885,73	2508,86		3
			235°5,91’	208,19	-6 -119,12	+6 -170,74	-119,18	-170,68
4	+0,3 114°39,0’	114°39,3’							766,55	2338,18		4
			300°26,61’	161,44	-4 81,80	+4 -139,18	81,76	-139,14
5	+0,3 120°05,5’	120°05,8’							848,31	2199,04		5
			0°20,81’	151,73	-4 151,73	+4 0,92	151,69	0,96
ПП-11	+0,3 112°40,5’	112°40,8’							1000	2200		ПП-11
			67°40,01’
2
∑	539°58,5’	540°00,0’		952	0,26	-0,26	0	0

---

3. Уравнивание горизонтальных углов

Уравнение углов выполняют в графах 2, 3 таблицы 1 в следующем порядке:

• 
  Вычисляют сумму измеренных углов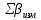 результат записывают в суммарной строке графы 2.
  

• 
  Вычисляют теоретическое значение этой суммы по формуле:
  

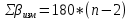, где n - число точек хода

• 
  Вычисляют угловую невязку хода:
  

• 
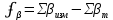
  Вычисляют допустимое значение этой невязки:
  

• 
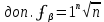
  Сравнивают полученную невязку с допустимой. Если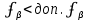 , то невязку распределяют поровну с обратным знаком на все измеренные углы, т.е. вычисляют поправки 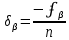. Эти поправки, округленные до, выписываются над измерительными углами. Контроль вычисления поправок .
  

• 
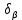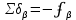
  В графе 3 вычисляют уравненные значения углов и их сумму. Сумма уравненных углов должна точно равняться .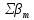
  

В заключении имеем следующие вычисления:

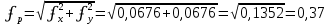
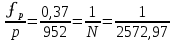
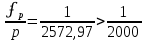
4. Вычисление дирекционных углов сторон хода

Дирекционные углы хода вычисляют в графе 4 таблицы 1 по дирекционному углу начальной стороны и уравненным значениями горизонтальных углов (правых) по формуле передачи дирекционного угла.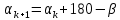



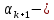дирекционный угол последующей стороны ход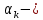

---

дирекционный угол предыдущей стороны

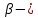правый по ходу горизонтальный угол между этими сторонами

При превышении значения дирекционного угла отметки 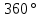из полученного значения следует вычесть .

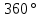Контроль вычислений:

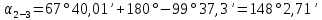
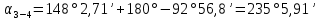
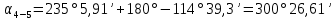
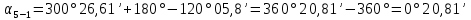
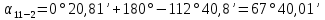
5. Вычисление и уравнивание приращений координат

Данные вычисления выполняются в графах 6-9 в таблице 1. Приращения координат вычисляются с помощью микрокалькуляторов по формулам:

∆x=d*cosα

∆y=d*sinα

d - горизонтальное проложение хода

α - дирекционный угол той же стороны

Вычисленные значения приращений округляют до 0,01 м и со своими знаками вписываются в 6, 7 графы таблицы 1. В суммарной строке этих графов записывают суммы приращений координат , .

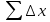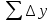Отличные вычисленных сумм от нуля есть невязки в приращениях координат ʄ_x и ʄ_y :

ʄ_x=

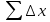
ʄ_x=

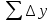
которые вызваны накоплением погрешностей измерения углов и линий.

Для оценки допустимых координатных невязок ʄ_x и ʄ_y вычисляют невязку ʄ_p в периметре хода и относительную невязку хода 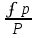по формулам: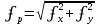







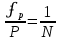
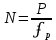
В нашем случае мы получаем следующие значения:

---

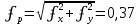
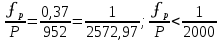
Относительную невязку выражают дробью с числителем, равным 1. Сравниваем полученную относительную невязку с допустимым значением. В нашей работе допустимую относительную невязку хода принимаем равной 1/2000. Если относительная невязка допустима, то координатные невязки ʄ_y и ʄ_x распределяют с обратным знаком по всем приращениям пропорционально длинам сторон хода d_i, т.е. вычисляют поправки δx и δy по формулам прямой пропорциональной зависимости:





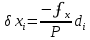
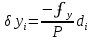
При вычислении поправок следует помнить, что дробь в формулах – постоянный коэффициент, а в самой поправке будет не более одной значащей цифры. Поправки δx и δy в сантиметрах вписывают над приращениями координат в графах 6 и 7 таблицы 1. Контроль вычисления поправок:





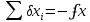
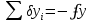
В графах 8 и 9 таблицы 1 вычисляют уравненные значения 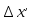, 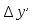приращений координат, учитывая знаки приращений и поправок: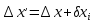





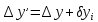
Контроль вычислений: суммы уравненных приращений координат должны точно равняться нулю, в противном случае нужно перепроверить вычисления.

6. Вычисление координат точек хода

По заданным координатам точки ПП-11 и уравненным приращением координат вычисляют координаты всех точек хода по формулам:




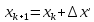
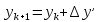
Контроль вычислений: все приращения координат взятых из граф 8 и 9 таблицы 1, получаются снова координаты первой точки.

7. Нанесение на план точек теодолитного хода

---