ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Параметры и конструкция шкивов
5 Выбор конструкций корпусных деталей редуктора и их расчет
6 Выбор конструкции и ориентировочный расчет валов. Подбор параметров шпоночных соединений
7 Выбор подшипников качения и эскизная компоновка редуктора
8 Проверочные расчеты валов, подшипников, шпоночных соединений
(4.10)
где σH – действительное контактное напряжение, МПа;
Т1 – крутящий момент на валу червячного колеса, Н∙мм;
aW – межосевое расстояние, мм
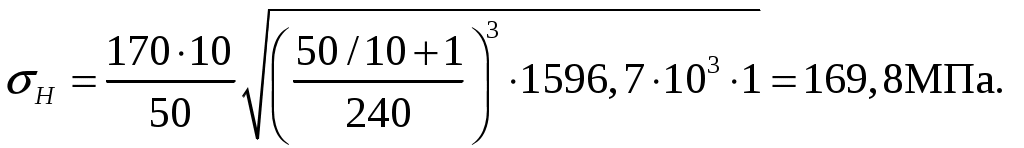
0,85[σН] ≤ σН ≤ 1,05 [σН], (4.11)
146 МПа < 169,8 МПа < 180,4 МПа.
Условие выполняется.
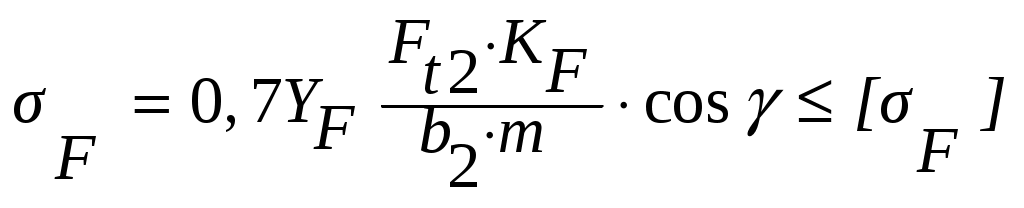 , (4.12)
, (4.12)
где F – действующее напряжение изгиба, МПа;
YF – коэффициент формы зуба,
YF = 1,45 [1, с.63, таблица 5.7],
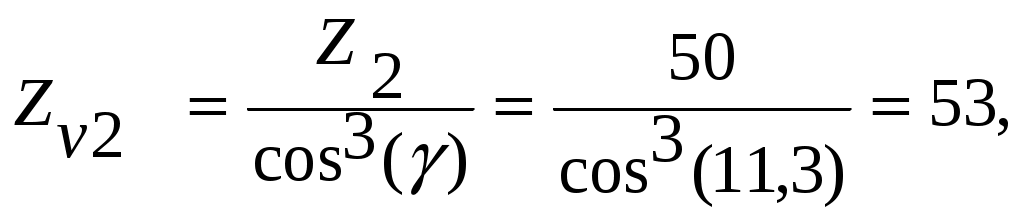 (4.13)
(4.13)
где Ft2 – окружное усилие на колесе;
d2 – делительный диаметр колеса;
da1 – диаметр вершин червяка;
b2 – ширина венца червячного колеса, которая зависит от диаметра вершин;
KF – коэффициент нагрузки;
Т2 – крутящий момент на валу червячного колеса, Н∙м.
KF = 1,1.

b2 = 0,75 · (d1 + 2 · m), (4.14)
b2 = 0,75 · (80 + 2 · 8) = 72 мм.
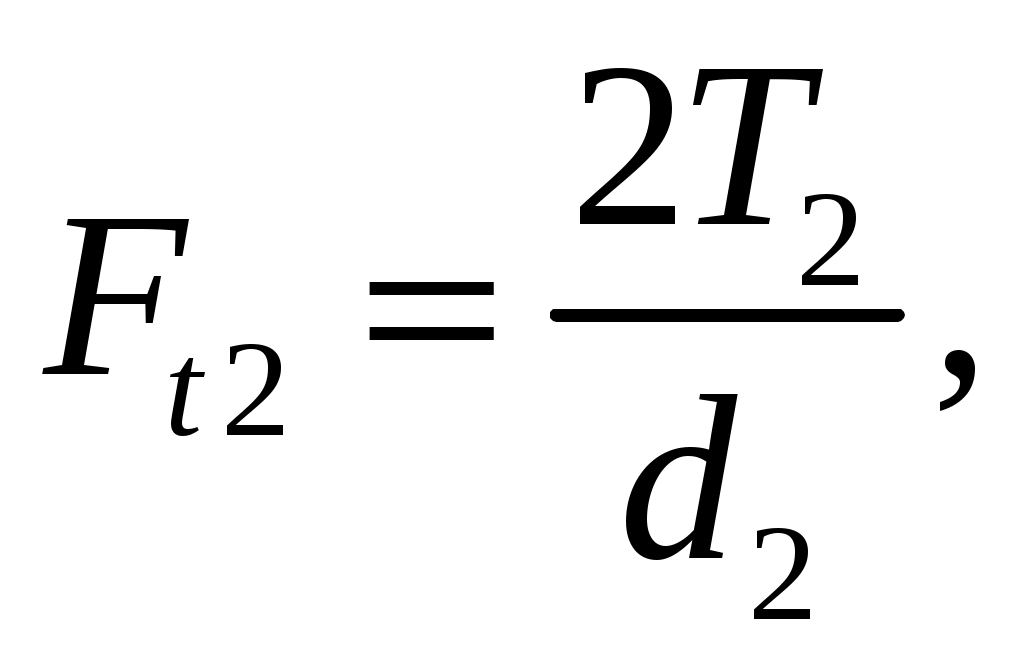 (4.15)
(4.15)
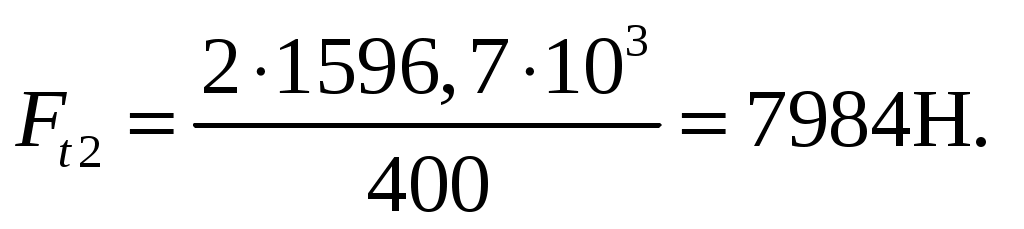
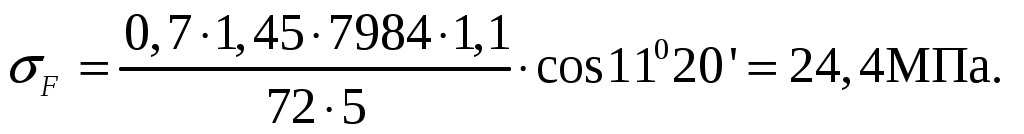
σF] = (0,08 · σв + 0,25 · σт) · KFL = 51 МПа, (4.16)
σF ≤ [σF], (4.17)
24,4 МПа < 51 МПа.
Условие выполняется.
При этом необходимо, чтобы действительное напряжение было F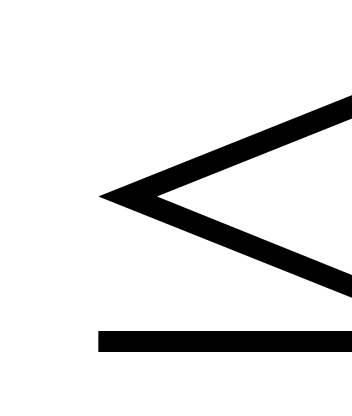 FP (допускается перегрузка до 5%, недогрузка не ограничивается). Поскольку σF<<σFP, значит, условие выполняется.
FP (допускается перегрузка до 5%, недогрузка не ограничивается). Поскольку σF<<σFP, значит, условие выполняется.
4.5 Определение параметров червячной передачи
Диаметры делительные (рисунок 4.1):
d1 = q·m, (4.18)
d1 = 8·10 =80 мм.


Рисунок 4.1 – Геометрические параметры червячной передачи
d2 = m·
Z2, (4.19)
d2 = 8
·50=400 мм.
Диаметры вершин:
da= m(q+ 2), (4.20)
da1 = 8(10+ 2) = 96 мм,
da2 = 8(50+ 2)=416 мм.
Диаметры впадин:
df = m(q– 2,4) =60,8 мм, (4.21)
df1 = 8(10– 2,4) =60,8 мм,
df2 = 8(50– 2,4) =380,8 мм.
Наружный диаметр колеса:
dam2 = da2 + 1,5m =428 мм, (4.22)
dam2 = 416 + 1,5·8 =428 мм.
Длина нарезной части червяка:
b1 = (11 + 0,1 ∙ Z2) m, (4.23)
b1 = (11 + 0,1∙ 50) 8 =128 мм.
Т.к. червяк шлифованный, то принимаем b1=147 мм.
Ширина венца червячного колеса:
b 2 = 0,75da1, (4.24)
b 2 = 0,75∙ 96 =72 мм.
Толщина обода (венца) червячного колеса:
a = 3m, (4.25)
a = 3∙8 =24 мм.
Длина ступицы:
lст= 1,1dв , (4.26)
lст= 1,1∙75 = 80 мм
где dв – диаметр вала под ступицей колеса,

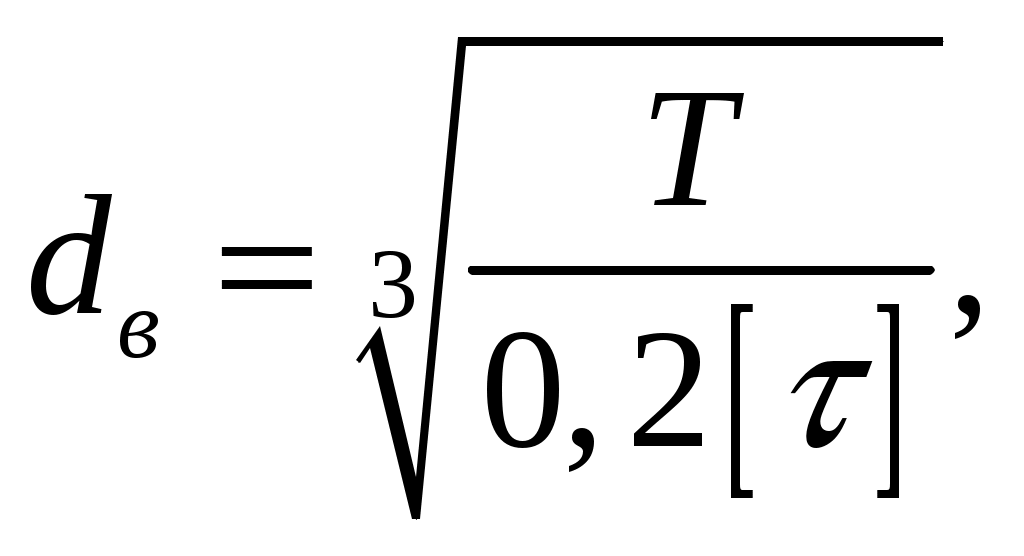 (4.27)
(4.27)
 где Т2 – крутящий момент на валу червячного колеса,
где Т2 – крутящий момент на валу червячного колеса,
[τk] – пониженное допускаемое напряжение кручения,
Т2 = 1596,7 Н∙м; [τk] = 20 МПа.
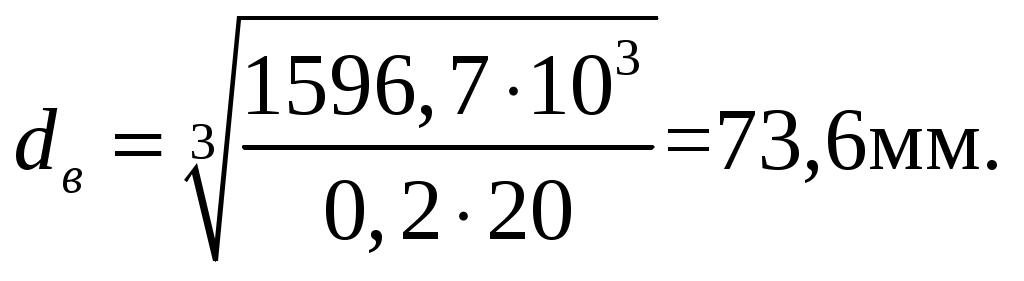
Принимаем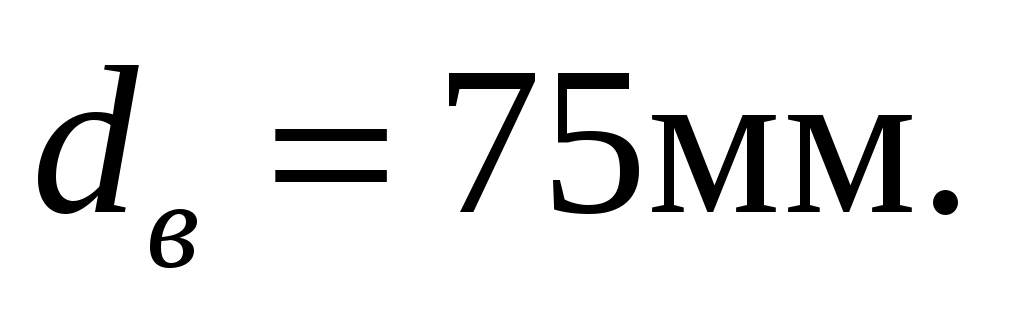
Диаметр ступицы:
dcт = 1,4dв , (4.28)
dcт = 1,4∙75=105 мм
Толщина диска, связывающего ступицу и обод:
с = 1,1а , (4.29)
с = 1,1∙24=26 мм.
Диаметр отверстий в диске:
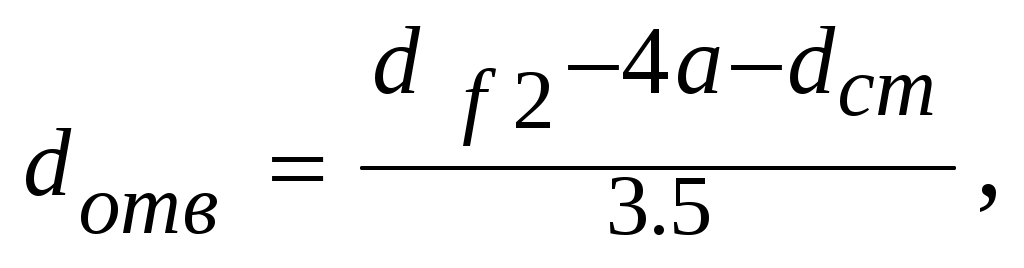
(4.30)
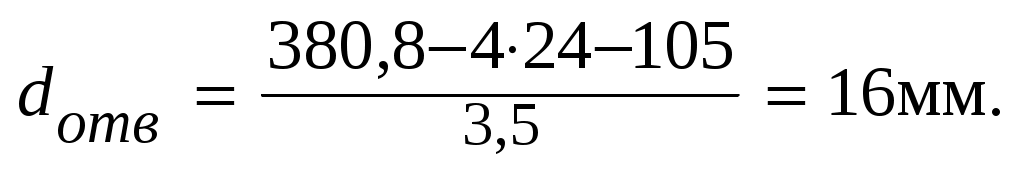
Диаметр винта (болта):
dвинт = 0,6 ∙ а , (4.31)
dвинт = 0,6 ∙ 24 = 16 мм.
Длина винта (болта):
Lвинта=2 ∙ а , (4.32)
Lвинта=2 ∙ 24 = 32 мм.
На торцах зубьев выполняются фаски размером 4 мм под углом α = 45º.
4.6 Силы в зацеплении
Определение усилий в зацеплении червячной передачи необходимо для расчета валов и подбора подшипников (рисунок 4.2).
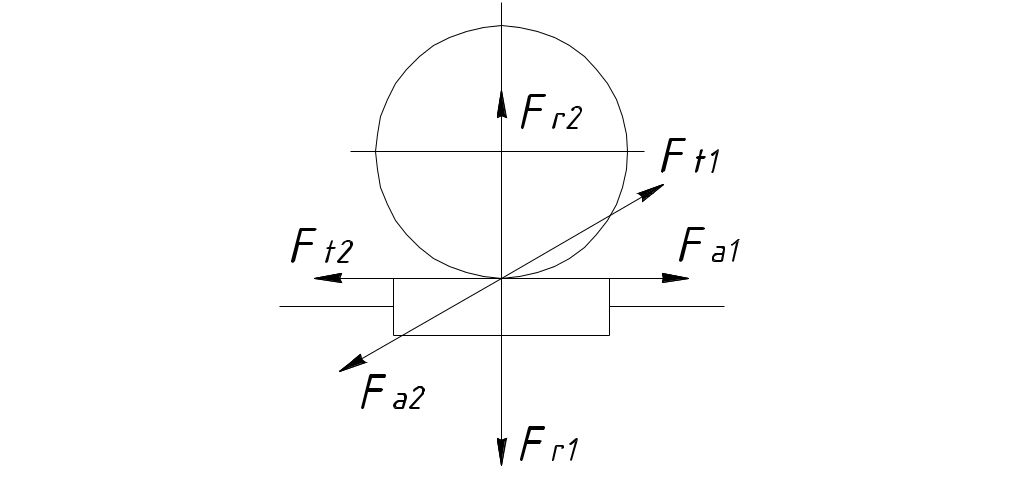
Рисунок 4.2 – Силы в червячной передаче
Окружное усилие на червяке Ft1 равно осевому усилию на червячном колесе Fa2:
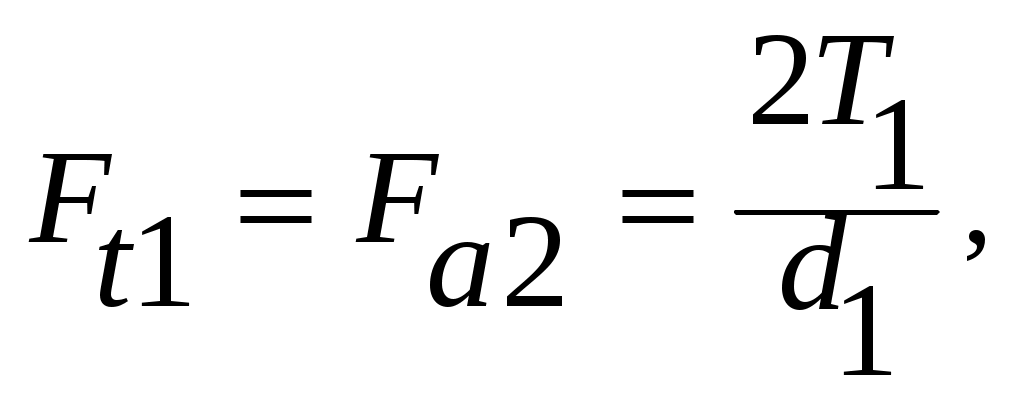 (4.33)
(4.33)

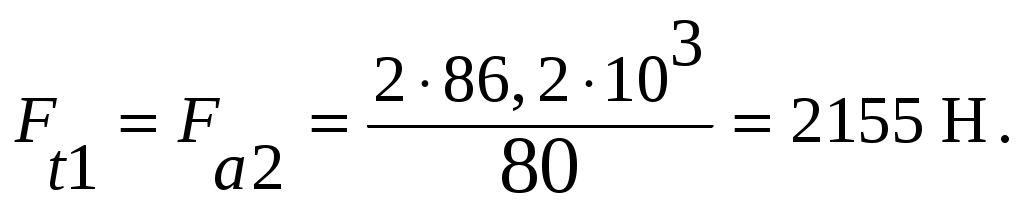
Окружное усилие на червячном колесе Ft2 равно осевому усилию на червяке Fa1:
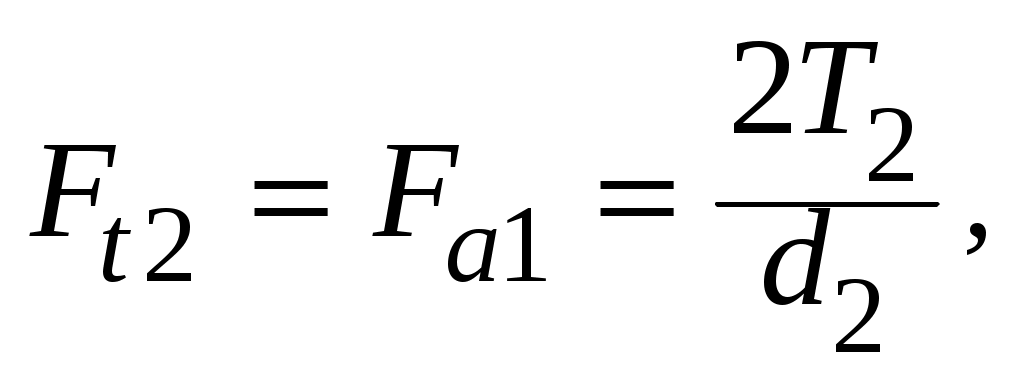 (4.34)
(4.34)
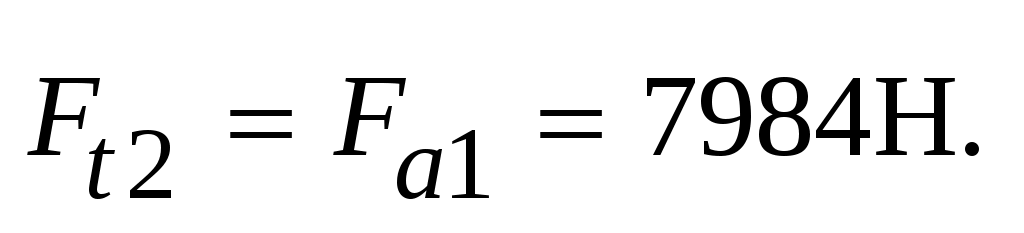
Радиальное усилие на червяке Fr1 равно радиальному усилию на червячном колесе Fr2:
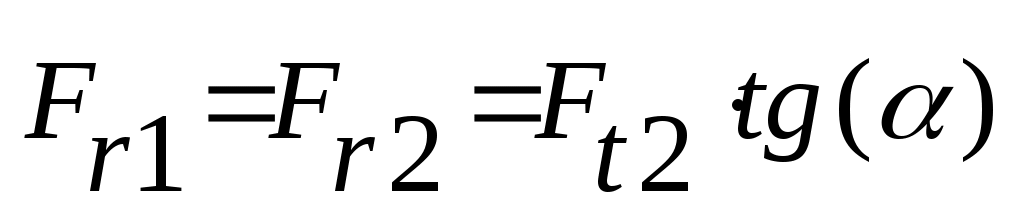 , (4.35)
, (4.35)
где = 20 – угол профиля,
Fr1 = Fr2 = 7984 ∙ tg(20º) = 2906 Н.
 4.7 Расчет вала червяка на жесткость
4.7 Расчет вала червяка на жесткость
Правильность зацепления червячной пары обеспечивает достаточная жесткость червяка. Критерием жесткости является значение прогиба f (мм) в среднем сечении червяка, которое не должно превышать допустимого f [f], обычно принимают [f] = (0,005-0,010)m;
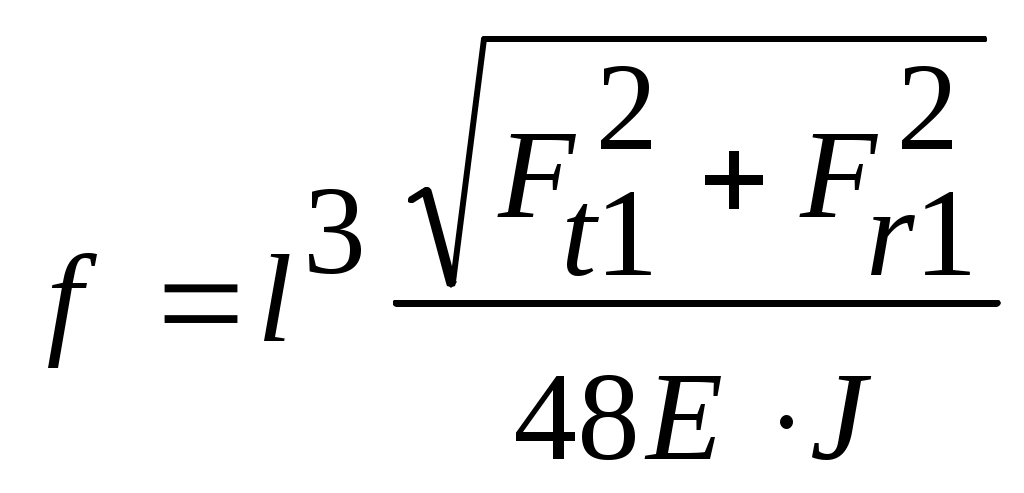 , (4.36)
, (4.36)
где L– расстояние между опорами, принимают из компоновки редуктора;
Е – модуль упругости.
Е = 2·105 МПа.
L=0,9 ∙ d2,
L= 0,9∙400= 360 мм,
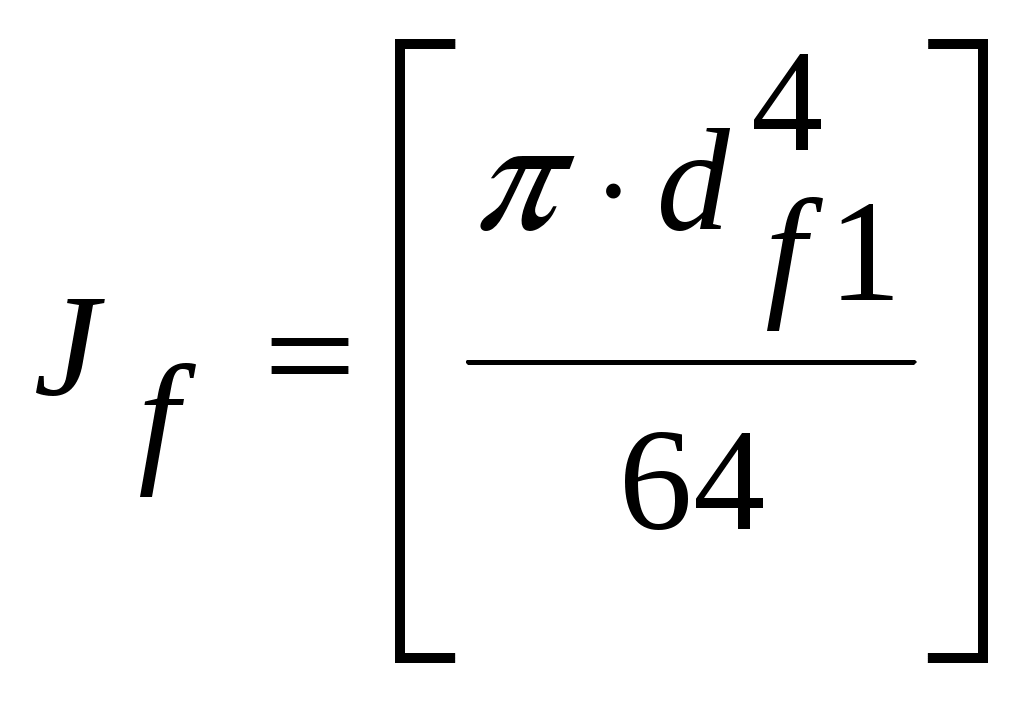 , (4.37)
, (4.37)
J=Jf∙ φ,
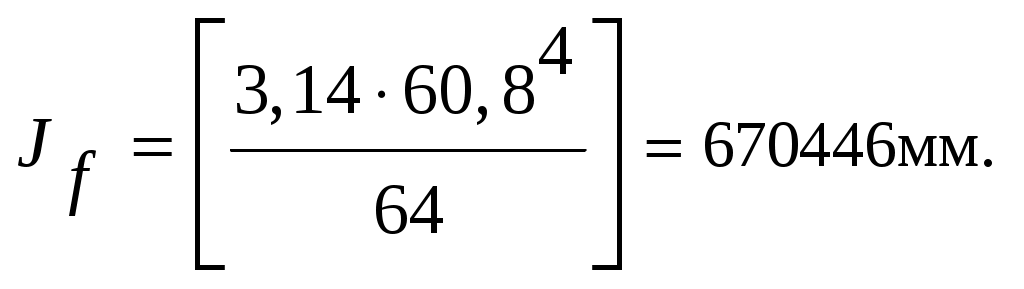
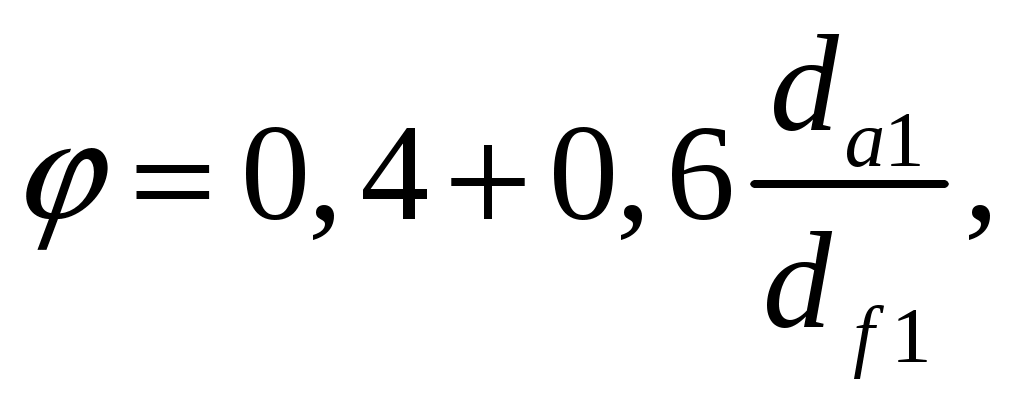 (4.38)
(4.38)
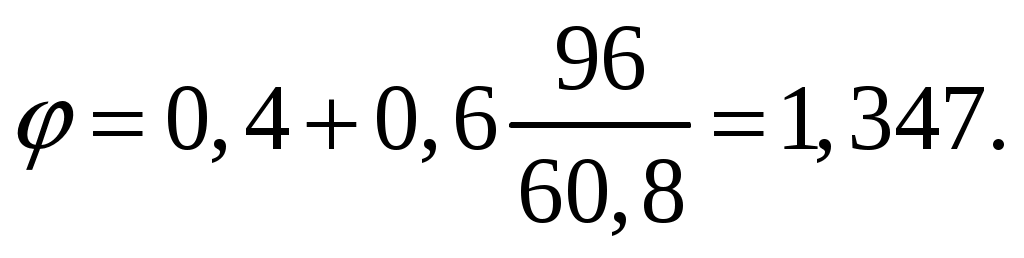
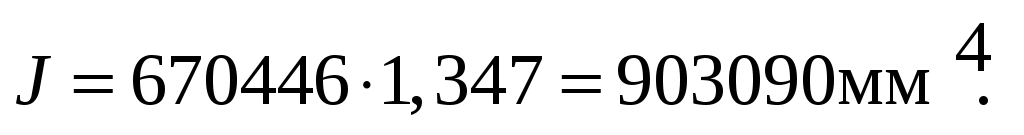
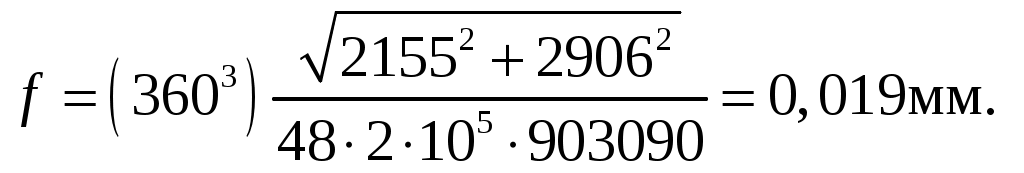
[f] = 0,030 мм.
0,019 мм < 0,030 мм.
Из проведенного расчета можно сделать вывод о том, что условие жесткости вала-червяка выполняется.
 4.8 Тепловой расчет червячного редуктора
4.8 Тепловой расчет червячного редуктора
При работе червячной передачи значительная часть мощности расходуется на преодоление трения, в результате чего происходит нагревание редуктора. Выделяемое тепло отводится в окружающую среду через стенки редуктора. В случае недостаточного отвода тепла редуктор перегревается и выходит из строя. Поэтому необходимо производить тепловой расчет с целью определения температуры масла, которая не должна превышать допускаемой величины. Температуру масла определяют по формуле:
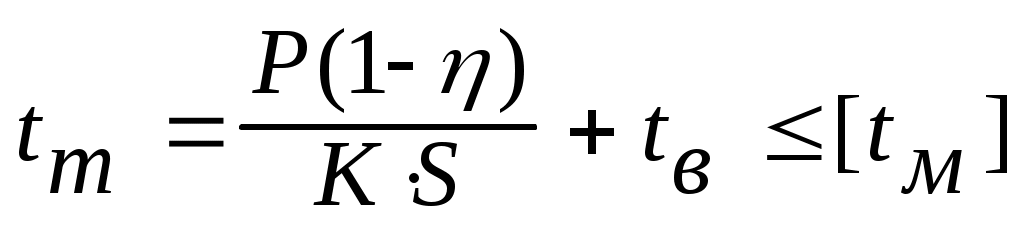 , (4.39)
, (4.39)
где [tм] – допускаемая температура масла;
P – мощность, подводимая к редуктору;
tв – температура окружающей среды;
K– коэффициент теплопередачи, который принимается с учетом параллельности осей редуктора и двигателя;
S – площадь поверхности охлаждения (равна площади поверхности всех стенок редуктора, которая снаружи омывается свободно циркулирующим воздухом.
[tм] = 60-90С [1, c.63]; tв = 20С [1, c.63];K = 32 Вт/м2·град [1, c.63];
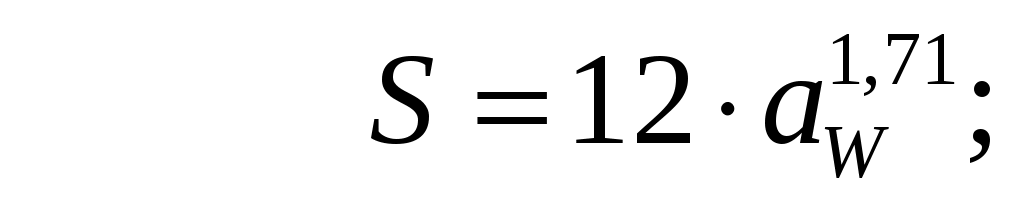 (4.40)
(4.40)
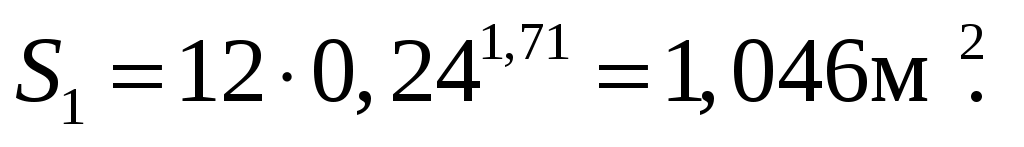
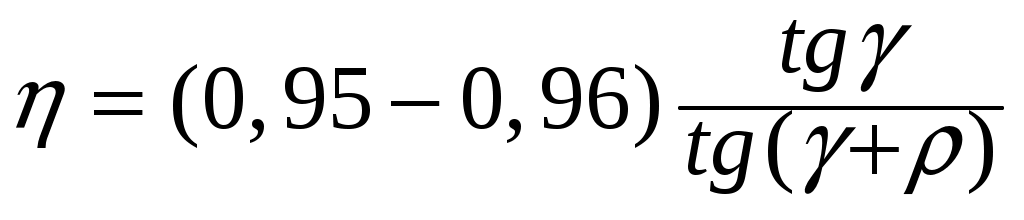 , (4.41)
, (4.41)
где ´ – приведенный угол трения, выбирают в зависимости от скорости скольжения;
– угол подъема винтовой линии червяка.
´ = 215´ [1, c.64],
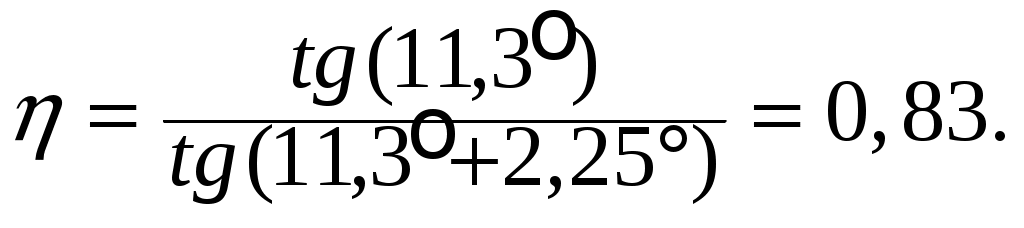
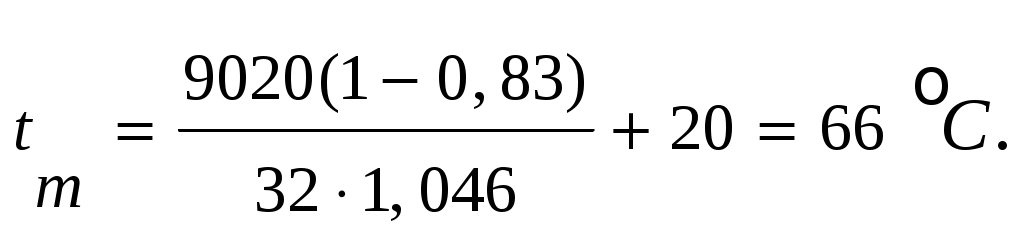
Температура масла в пределах допустимой. Условие выполняется.
где σH – действительное контактное напряжение, МПа;
Т1 – крутящий момент на валу червячного колеса, Н∙мм;
aW – межосевое расстояние, мм
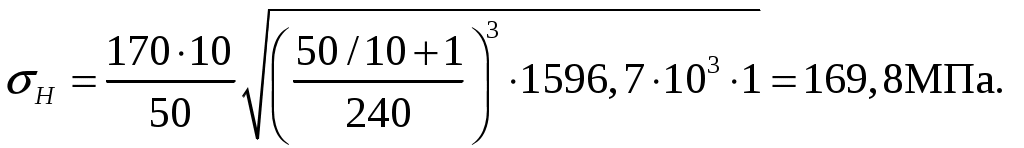
0,85[σН] ≤ σН ≤ 1,05 [σН], (4.11)
146 МПа < 169,8 МПа < 180,4 МПа.
Условие выполняется.
4.4 Проверочный расчет на выносливость при изгибе
Условия прочности по напряжениям изгиба зубьев червячного колеса:
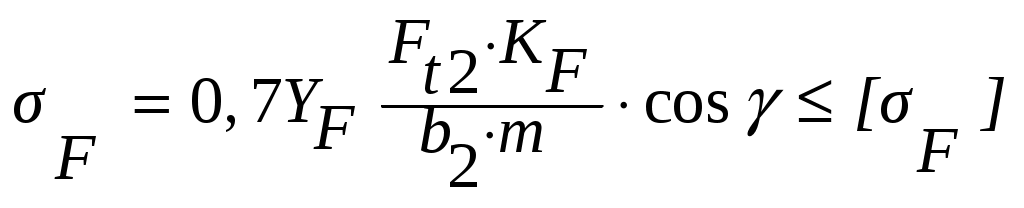 , (4.12)
, (4.12)где F – действующее напряжение изгиба, МПа;
YF – коэффициент формы зуба,
YF = 1,45 [1, с.63, таблица 5.7],
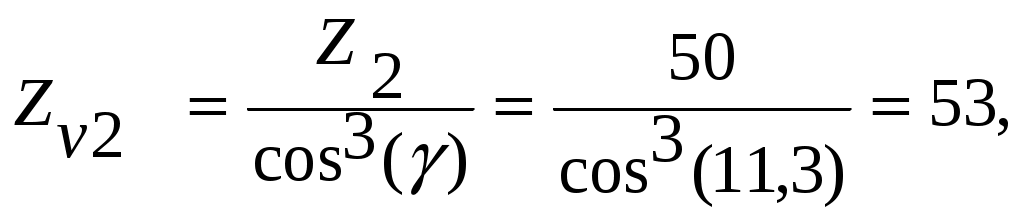 (4.13)
(4.13)где Ft2 – окружное усилие на колесе;
d2 – делительный диаметр колеса;
da1 – диаметр вершин червяка;
b2 – ширина венца червячного колеса, которая зависит от диаметра вершин;
KF – коэффициент нагрузки;
Т2 – крутящий момент на валу червячного колеса, Н∙м.
KF = 1,1.

b2 = 0,75 · (d1 + 2 · m), (4.14)
b2 = 0,75 · (80 + 2 · 8) = 72 мм.
σF] = (0,08 · σв + 0,25 · σт) · KFL = 51 МПа, (4.16)
σF ≤ [σF], (4.17)
24,4 МПа < 51 МПа.
Условие выполняется.
При этом необходимо, чтобы действительное напряжение было F
4.5 Определение параметров червячной передачи
Диаметры делительные (рисунок 4.1):
d1 = q·m, (4.18)
d1 = 8·10 =80 мм.


Рисунок 4.1 – Геометрические параметры червячной передачи
d2 = m·
Z2, (4.19)
d2 = 8
·50=400 мм.
Диаметры вершин:
da= m(q+ 2), (4.20)
da1 = 8(10+ 2) = 96 мм,
da2 = 8(50+ 2)=416 мм.
Диаметры впадин:
df = m(q– 2,4) =60,8 мм, (4.21)
df1 = 8(10– 2,4) =60,8 мм,
df2 = 8(50– 2,4) =380,8 мм.
Наружный диаметр колеса:
dam2 = da2 + 1,5m =428 мм, (4.22)
dam2 = 416 + 1,5·8 =428 мм.
Длина нарезной части червяка:
b1 = (11 + 0,1 ∙ Z2) m, (4.23)
b1 = (11 + 0,1∙ 50) 8 =128 мм.
Т.к. червяк шлифованный, то принимаем b1=147 мм.
Ширина венца червячного колеса:
b 2 = 0,75da1, (4.24)
b 2 = 0,75∙ 96 =72 мм.
Толщина обода (венца) червячного колеса:
a = 3m, (4.25)
a = 3∙8 =24 мм.
Длина ступицы:
lст= 1,1dв , (4.26)
lст= 1,1∙75 = 80 мм
где dв – диаметр вала под ступицей колеса,

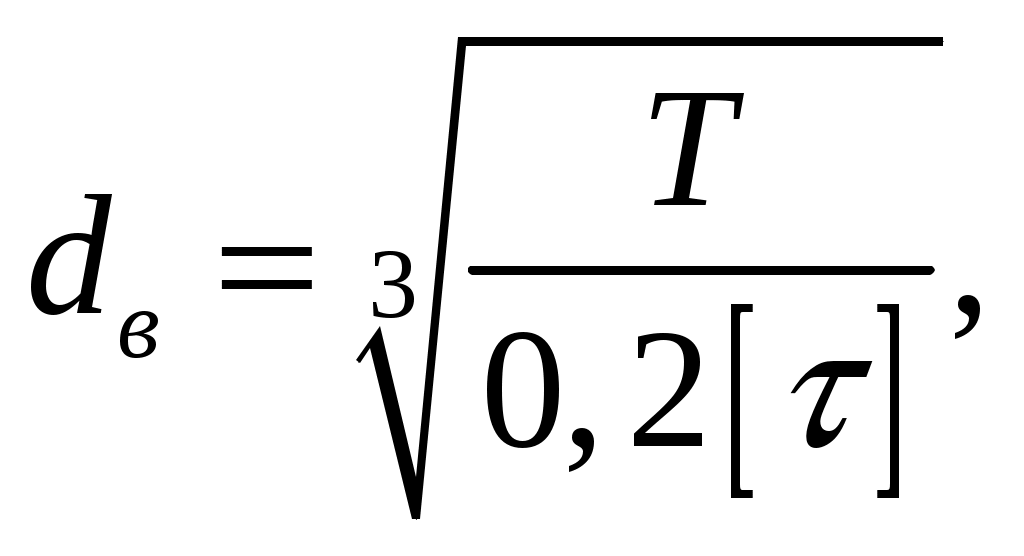 (4.27)
(4.27) где Т2 – крутящий момент на валу червячного колеса,
где Т2 – крутящий момент на валу червячного колеса,[τk] – пониженное допускаемое напряжение кручения,
Т2 = 1596,7 Н∙м; [τk] = 20 МПа.
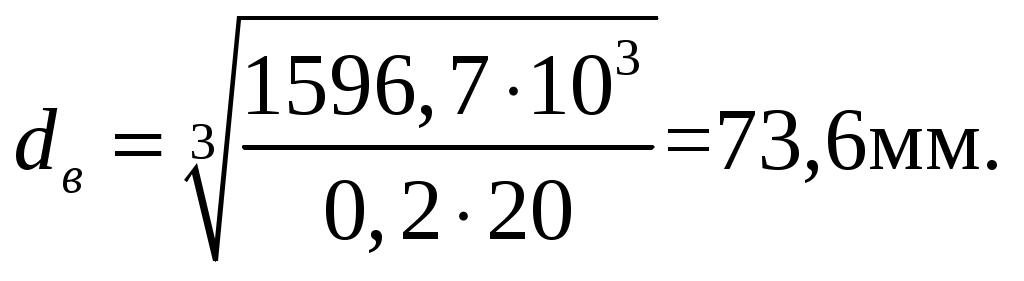
Принимаем
Диаметр ступицы:
dcт = 1,4dв , (4.28)
dcт = 1,4∙75=105 мм
Толщина диска, связывающего ступицу и обод:
с = 1,1а , (4.29)
с = 1,1∙24=26 мм.
Диаметр отверстий в диске:
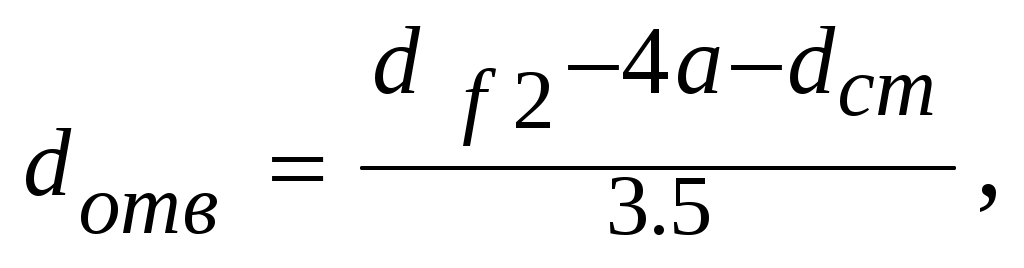
(4.30)
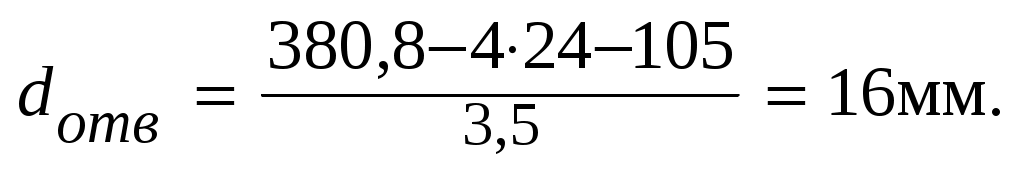
Диаметр винта (болта):
dвинт = 0,6 ∙ а , (4.31)
dвинт = 0,6 ∙ 24 = 16 мм.
Длина винта (болта):
Lвинта=2 ∙ а , (4.32)
Lвинта=2 ∙ 24 = 32 мм.
На торцах зубьев выполняются фаски размером 4 мм под углом α = 45º.
4.6 Силы в зацеплении
Определение усилий в зацеплении червячной передачи необходимо для расчета валов и подбора подшипников (рисунок 4.2).

Рисунок 4.2 – Силы в червячной передаче
Окружное усилие на червяке Ft1 равно осевому усилию на червячном колесе Fa2:
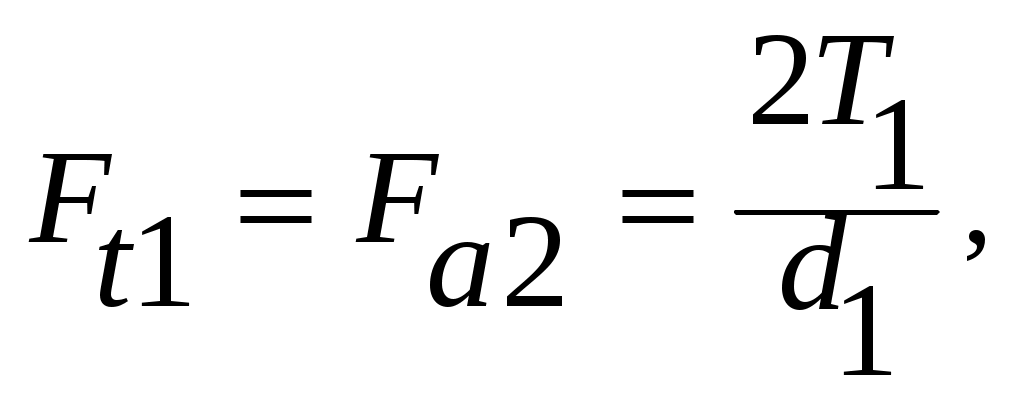 (4.33)
(4.33)
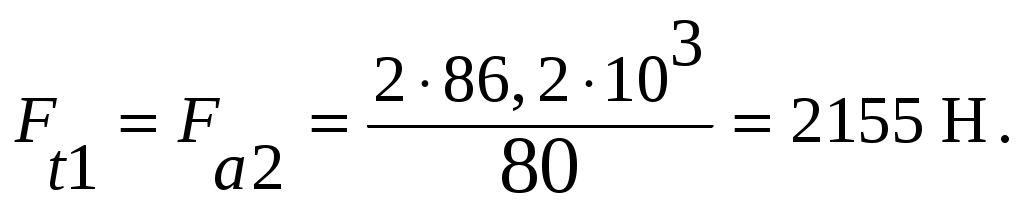
Окружное усилие на червячном колесе Ft2 равно осевому усилию на червяке Fa1:
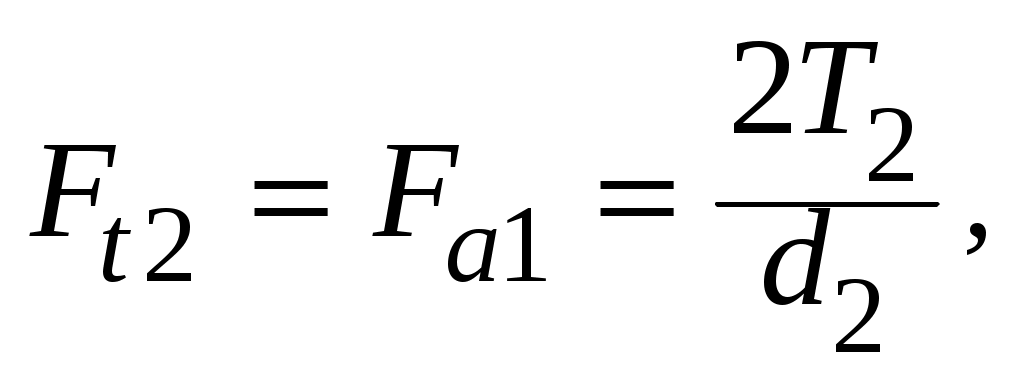 (4.34)
(4.34)Радиальное усилие на червяке Fr1 равно радиальному усилию на червячном колесе Fr2:
где = 20 – угол профиля,
Fr1 = Fr2 = 7984 ∙ tg(20º) = 2906 Н.
 4.7 Расчет вала червяка на жесткость
4.7 Расчет вала червяка на жесткостьПравильность зацепления червячной пары обеспечивает достаточная жесткость червяка. Критерием жесткости является значение прогиба f (мм) в среднем сечении червяка, которое не должно превышать допустимого f [f], обычно принимают [f] = (0,005-0,010)m;
где L– расстояние между опорами, принимают из компоновки редуктора;
Е – модуль упругости.
Е = 2·105 МПа.
L=0,9 ∙ d2,
L= 0,9∙400= 360 мм,
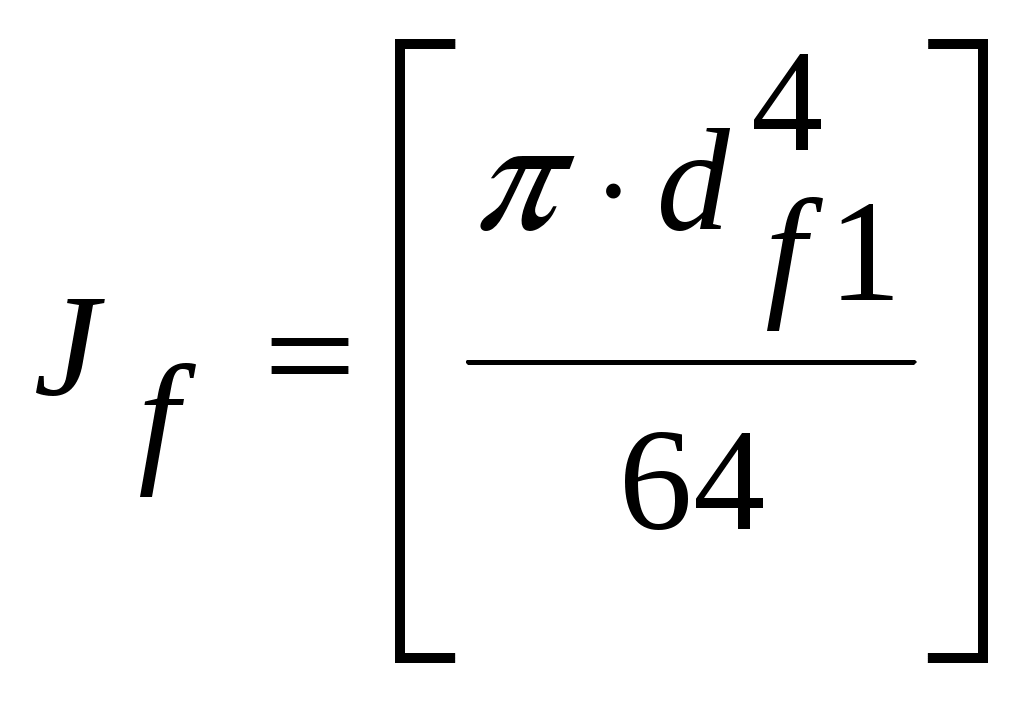 , (4.37)
, (4.37)J=Jf∙ φ,
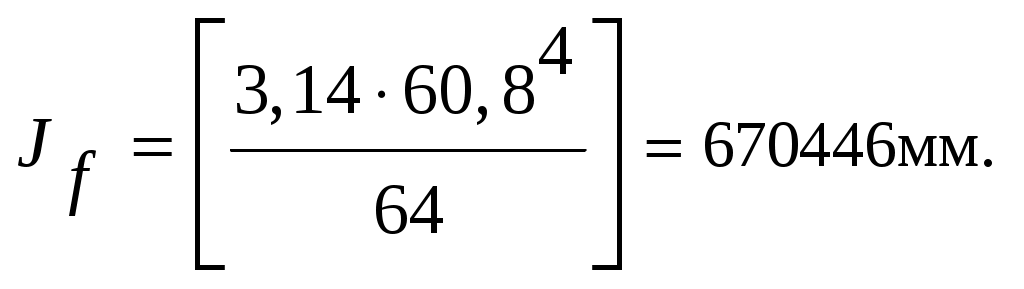
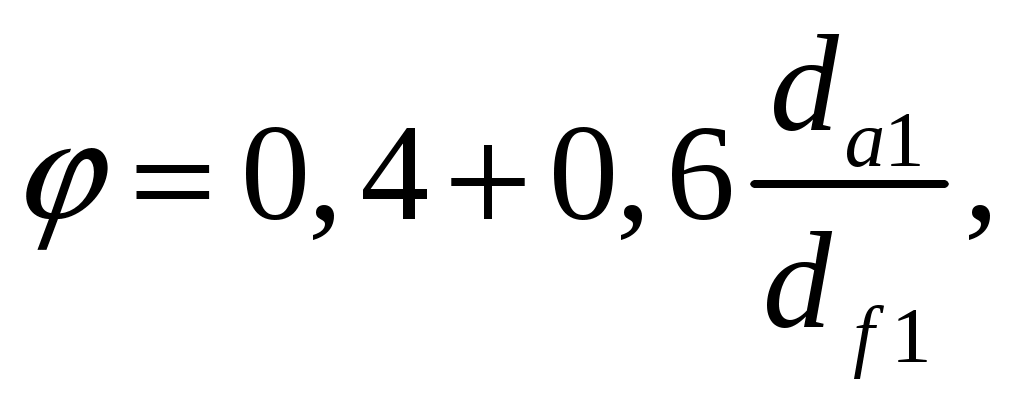 (4.38)
(4.38)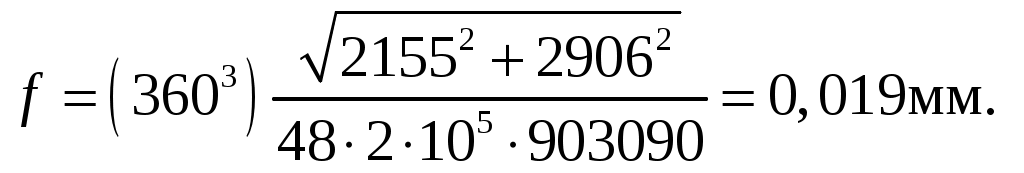
[f] = 0,030 мм.
0,019 мм < 0,030 мм.
Из проведенного расчета можно сделать вывод о том, что условие жесткости вала-червяка выполняется.
 4.8 Тепловой расчет червячного редуктора
4.8 Тепловой расчет червячного редуктораПри работе червячной передачи значительная часть мощности расходуется на преодоление трения, в результате чего происходит нагревание редуктора. Выделяемое тепло отводится в окружающую среду через стенки редуктора. В случае недостаточного отвода тепла редуктор перегревается и выходит из строя. Поэтому необходимо производить тепловой расчет с целью определения температуры масла, которая не должна превышать допускаемой величины. Температуру масла определяют по формуле:
где [tм] – допускаемая температура масла;
P – мощность, подводимая к редуктору;
tв – температура окружающей среды;
K– коэффициент теплопередачи, который принимается с учетом параллельности осей редуктора и двигателя;
S – площадь поверхности охлаждения (равна площади поверхности всех стенок редуктора, которая снаружи омывается свободно циркулирующим воздухом.
[tм] = 60-90С [1, c.63]; tв = 20С [1, c.63];K = 32 Вт/м2·град [1, c.63];
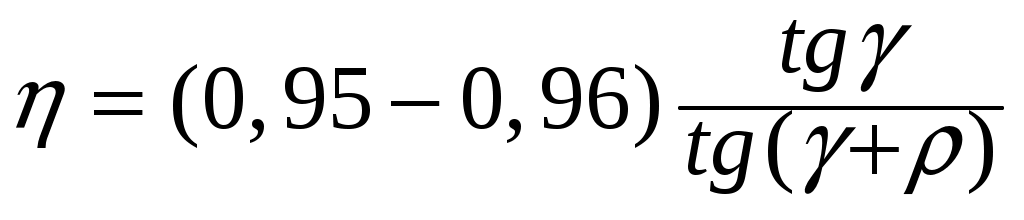 , (4.41)
, (4.41)где ´ – приведенный угол трения, выбирают в зависимости от скорости скольжения;
– угол подъема винтовой линии червяка.
´ = 215´ [1, c.64],
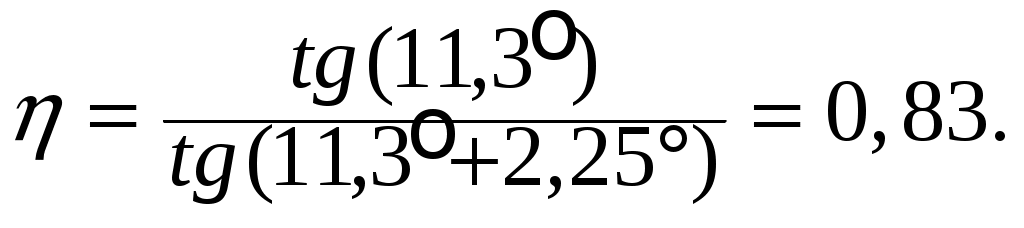
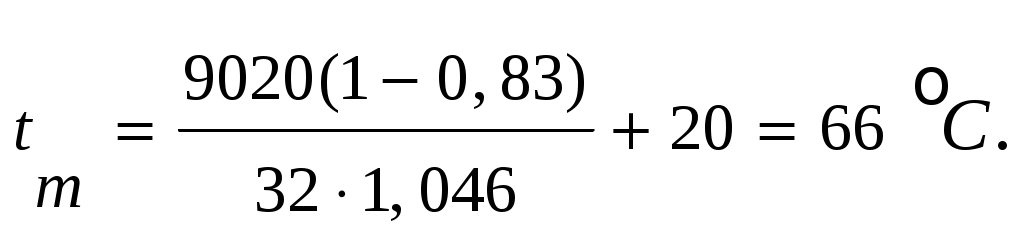
Температура масла в пределах допустимой. Условие выполняется.
