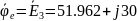Файл: асчет разветвленных электрических цепей однофазного синусоидального тока.docx
Добавлен: 02.02.2019
Просмотров: 532
Скачиваний: 7
Министерство Образования и Науки Республики Казахстан
Некоммерческое акционерное общество
Алматинский Университет Энергетики и Связи
Кафедра ТОЭ
РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА №3
По дисциплине: «Теоретические основы электротехники 1»
На тему: «Расчет разветвленных электрических цепей однофазного синусоидального тока»
Специальность: 050718 Электроэнергетика
Выполнила: Наурзбаева С. Группа: Э-13-7
№ зачетной книжки: 134228
Принял: старший преподаватель Креслина C.Ю.
________ «___» ___________ 2014 г. ________
Алматы 2014
3.1 Система уравнений по законам Кирхгофа для значений токов. 4
3.2 Расчет комплексных действующих значений токов 5
б) Метод узловых потенциалов 8
3.3 Уравнение баланса мощностей 9
Содержание:
1. Цель работы
2. Исходные данные
3. Решение
3.1 Система уравнений по законам Кирхгофа для значений токов.
3.2 Расчет комплексных действующих значений токов
а) Метод контурных токов
б) Метод узловых потенциалов
3.3 Уравнение баланса мощностей
3.4 Топографическая диаграмма
Список используемой литературы.
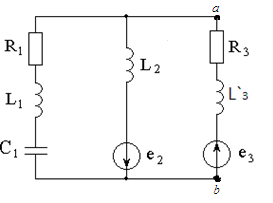
Для разветвленной электрической цепи выполнить следующее:
а) составить систему уравнений по законам Кирхгофа для мгновенных значений токов и напряжений и для комплексных величин;
б) рассчитать комплексные действующие значения токов во всех ветвях двумя методами: методом контурных токов и методом узловых потенциалов;
в) составить уравнение баланса мощностей в цепи и проверить точность его выполнения;
г) построить топографическую диаграмму, совмещенную с векторной диаграммой токов.
Методические указания:
а) при расчёте методами контурных токов и узловых потенциалов схему можно упростить путём замены двух параллельных ветвей с пассивными элементами одной эквивалентной;
б) баланс мощностей можно составить для комплексной, активной и реактивной мощностей. Для полных мощностей уравнение баланса не составляется;
в) при построении топографической диаграммы точку с нулевым потенциалом следует поместить в начало координат на комплексной плоскости и из этой же точки строить вектора токов.
2. Исходные данные
Таблица 3.1 Таблица 3.2
|
Год поступления |
Предпоследняя цифра зачетной книжки |
|
Нечетный |
2 |
|
R1, Ом |
8 |
|
XL1, Ом |
8 |
|
XC1, Ом |
7 |
|
R2, Ом |
18 |
|
XL2, Ом |
10 |
|
XC2, Ом |
6 |
|
Год поступления |
Последняя цифра зачетной книжки |
|
Нечетный № рисунка |
8 3.9 |
|
Е1, В |
40 |
|
Ψe1, град |
60 |
|
Е2, В |
0 |
|
Ψe2, град |
0 |
|
Е3, В |
60 |
|
Ψe3, град |
30 |
Т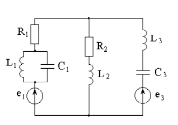
аблица
3.3
|
Год поступления |
Первая буква фамилии |
|
четный |
Н |
|
R3, Ом |
16 |
|
XL3, Ом |
20 |
|
XC3, Ом |
15 |
Рисунок 3.1
3. Решение
3.1 Система уравнений по законам Кирхгофа для значений токов.
С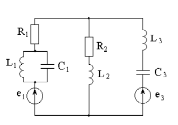
оставим
систему уравнений по законам Кирхгофа
для мгновенных и комплексных значений
токов:
Рисунок 3.2
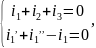 –
I
закон Кирхгофа для мгновенных значений
–
I
закон Кирхгофа для мгновенных значений
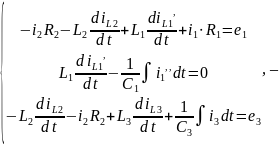
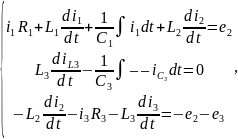 II
закон Кирхгофа для мгновенных значений
II
закон Кирхгофа для мгновенных значений
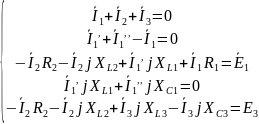 , – для
комплексных значений
, – для
комплексных значений
3.2 Расчет комплексных действующих значений токов
Рассчитаем комплексные действующие значения токов во всех ветвях двумя методами:
Для этого сначала произведем замену:
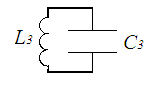
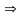
![]() L`3
L`3
Рисунок 3.3
где
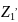 – общее сопротивление между L1
и С1
– общее сопротивление между L1
и С1
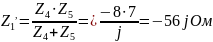
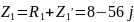
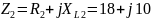
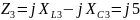
Тогда схема примет следующий вид:
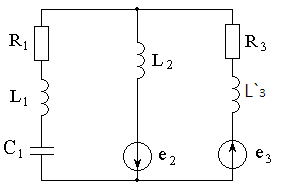
Рисунок 3.4
а) Метод контурных токов
Составим систему уравнений для контуров схемы:

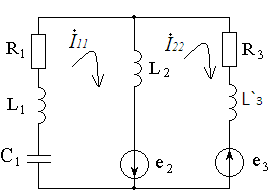
Рисунок 3.5
Далее с помощью вычислительной программы Mathcad13, подставив значения в систему, решим уравнение методом Крамера:
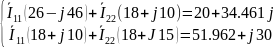
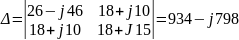
Δ11=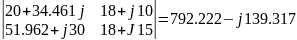
Δ22=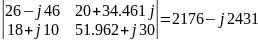
I11=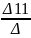 =
-0.417-j0.507
А
=
-0.417-j0.507
А
I22=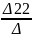 =
2.966 – j0.068
А
=
2.966 – j0.068
А
Отсюда следует, что:
I1= I11=-0.417-j0.507 А
I2= -(I11– I22)= -2.549+j0.573 А
I3= I22 = 2.966 – j0.068 А
Методом наложения найдем токи в параллельных ветвях:
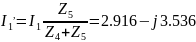
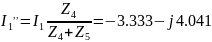
Проверим токи с помощью Iго закона Кирхгофа:
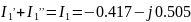
Переведя токи из алгебраической формы в показательную, а затем в мгновенные, получим:
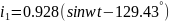
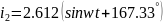
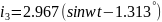
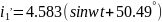
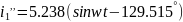
 б)
Метод узловых потенциалов
б)
Метод узловых потенциалов
Из
схемы видно, что
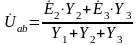 , где
, где
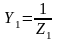
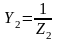
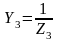 Рисунок
3.5
Рисунок
3.5
Тогда:
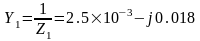 См
См
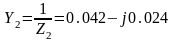 См
См
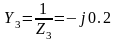 См
См
Подставив значения, получим:
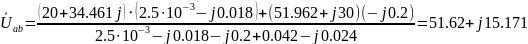 В
В
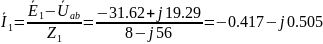 А
А
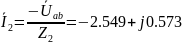 А
А
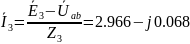 А
А
Проверим токи, полученные методом узловых потенциалов с помощью I закона Кирхгофа
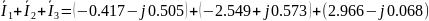 =0
=0
3.3 Уравнение баланса мощностей
Составим уравнение баланса мощностей в цепи и проверим точность его выполнения:
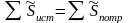
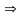
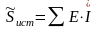
Тогда
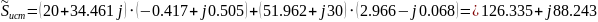 Вт
Вт
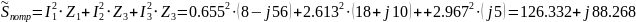 Вт
Вт
Определим
погрешность вычислений: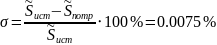
3.4 Топографическая диаграмма
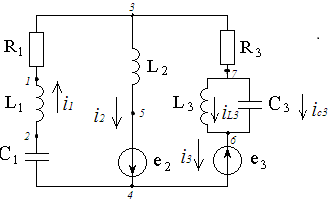
Рисунок 3.6
Пусть
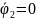 ,
тогда остальные потенциалы рассчитаем
с помощью Mathcad
,
тогда остальные потенциалы рассчитаем
с помощью Mathcad
-
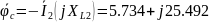 В
В
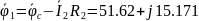 В
В
-
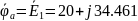 В
В
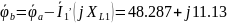 В
В
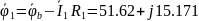 В
В
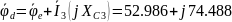 В
В
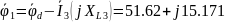 В
В
Список используемой литературы
-
Л.А. Бессонов «Теоретические основы электротехники. Электрические цепи»;
-
Л.Р. Нейман, К.С. Демирчян «Теоретические основы электротехники»;
-
Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. страхов «Основы теории цепей»;
-
Конспект лекций «Теоретические основы электротехники 1».