Добавлен: 02.02.2019
Просмотров: 5613
Скачиваний: 87
|
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ ШӘКӘРІМ атындағы СЕМЕЙ қаласының МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ |
||
|
3 деңгейлі СМЖ құжаты |
ПОӘК |
ПОӘК 042-14.01.20.168/03-2013 |
|
«Аналитикалық геометрия» пәніне арналған оқу-әдістемелік материалдар ПОӘК |
02.09.13 ж. №1 басылым |
|
ПӘННІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕНІ
«Аналитикалық геометрия»
5В050109 – «Математика» мамандығы үшін
ОҚУ -ӘДІСТЕМЕЛІК МАТЕРИАЛДАР
Семей
2013
Мазмұны
-
Глоссарийлар…………..…………………………………………………….3
-
Дәріс оқулар …………………………………………………………………5
-
Практикалық сабақтар........…………………………………………………36
-
Студенттің өздік жумысы...................………………………………………45
1 ГЛОССАРИЙ
|
№ |
Жаңа ұғымдар |
Мазмұны |
|
|
1 |
Екінші ретті анықтауыш |
|
|
|
2 |
Үшінші ретті анықтауыш |
|
|
|
3 |
Минор |
М23= |
|
|
4 |
Алгебралық толықтауыш |
Аij=(-1)i+j |
|
|
5 |
Матрица |
.
А= |
|
|
6 |
Кері матрица |
А-1 |
|
|
8 |
Вектор |
|
|
|
9 |
Скалярлық көбейтіндісі |
( ( cos
|
|
|
10 |
Векторлық көбейтіндісі |
с= S= |
|
|
11 |
Смешанное произведение |
( Егер
( V= |
|
|
12 |
Жазақтықтағы түзудін теңдеуі |
Ах+Ву+С=0 – жалпы теңдеу к=
A(x-x0)+B(y-y0)=0 – нормалі бар түзудің теңдеуі
y-y0=k(x-x0) – бұрыштық коэффициентпен берілген түзудің теңдеуі
к1 = к2 – түзулердің параллель шарты к1
= tg |
|
|
13 |
Екінші ретті қисықтар |
|
|
|
14 |
Кеңістіктегі тұзудің теңдеудің |
|
|
|
15 |
Жазықтықтың теңдеуі |
Ax+By+Cz+D=0 - Жалпы теңдеуі A(x-x0)+B(y-y0)+C(z-z0)=0,
где
d= |
|
2 ДӘрiстер
Сызықтық алгебра
1 – дәріс
Анықтама.
m
жатық және n тік жолдарда орналасқан
сандар кестесін m![]() n
өлшемді тік бұрышты А матрицасы деп
атайды. Яғни
n
өлшемді тік бұрышты А матрицасы деп
атайды. Яғни
А=![]()
Бізге
А=![]() екінші ретті квадрат матрица берілсін.
екінші ретті квадрат матрица берілсін.
Анықтама. Екінші ретті квадрат А матрицасына сәйкесті екінші ретті анықтауыш деп санды атайды және оны былайша белгілейді
![]() =а11а22
–
а21а12
=а11а22
–
а21а12
Мысал.
Мына анықтауышты
![]() есепте.
есепте.
Шешуі.
![]() =
=
![]() .
.
Үшінші ретті анықтауыш туралы түсінік
Анықтама. Үшінші ретті квадрат матрицаға сәйкесті үшінші ретті анықтауыш деп
а11 а22 а33 +а12 а11 а23 а31 +а13 а21 а32 -а13 а22 а31 -а12 а21 а33 -а11 а23 а32 санын атап, мына символ арқылы белгілейді:
![]() =
а11
а22
а33
+а12
а11
а23
а31
+а13
а21
а32
-а13
а22
а31
-а12
а21
а33
-а11
а23
а32
=
а11
а22
а33
+а12
а11
а23
а31
+а13
а21
а32
-а13
а22
а31
-а12
а21
а33
-а11
а23
а32
Үшінші ретті анықтауышты есептеуде Саррюс ережесін (үшбұрыш ережесін) қолданылады:
![]()













 =
=
![]() +
+
![]() +
+
![]() -
-
![]() -
-
![]() -
-
![]() .
.
Мысал.
Мына
анықтауышты
![]() есептеу
керек.
есептеу
керек.
Ол үшін үшбұрыш ережесін қолданамыз. Сонда
![]() =
=![]()
Анықтауыштың қасиеттері
-
Анықтауыштың жатық жолдарын оның сәйкес тік жолдарымен орын алмастырғаннан ол анықтауыштың сан мәні өзгермейді.
-
Егер анықтауыштың қандай болса да бір жатық жолының барлық элементтері нөлге тең болса, онда анықтауыш нөлге тең болады.
-
Егер анықтауыштың екі жатық жолын бірі мен бірінің орындарын алмастырсақ, онда анықтауыш таңбасы қарама - қарсы таңбаға ауысады.
-
Егер анықтауыштың кез келген екі жатық жолы өзара тең болса, онда ол нөлге тең болады.
-
Егер анықтауыштың қандай болмасын бір жатық жолының ортақ
 көбейткіші болса, онда оны (
көбейткіші болса, онда оны (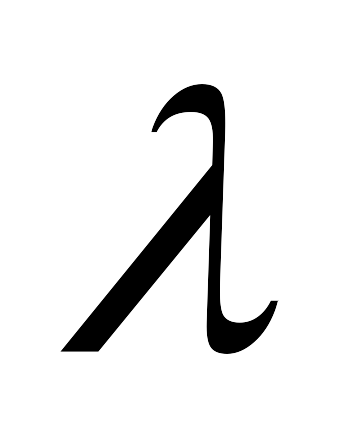 )
анықтауыш таңбасының алдына шығаруға
болады.
)
анықтауыш таңбасының алдына шығаруға
болады.
Алгебралық толықтауыштар мен минорлар
Анықтама. Үшінші ретті анықтауыштың аij элементінің Мij миноры деп анықтауыштың і - ші жатық жолын және j - ші тік жолын сызғанда калған элементтерінен құралған екінші ретті анықтауышты атайды.
Мысалы,
М23=![]()
Анықтама.
аij
элементінің
Aij
алгебралық толақтауышы деп оның (-1)i+j
таңбасымен алынған минорын айтады, яғни
Аij=(-1)i+j![]() Mij.
Mij.
Мысал.
Мына
анықтауыштың
![]() М12,
М31,
А22,
А12
табу керек.
М12,
М31,
А22,
А12
табу керек.
М12=![]() =24-2=22,
М31=
=24-2=22,
М31=![]() =6-20=-14,
=6-20=-14,
A22=(-1)2+2![]() =+(12+4)=16,
A12=(-1)1+2
=+(12+4)=16,
A12=(-1)1+2![]() =-(24-2)=-22.
=-(24-2)=-22.
Екі және үш белгісізді сызықтық теңдеулер жүйесі. Крамер формулалары.
Бізге үш белгісізді сызықтық үш тендеулер жүйесі берілсін:
a 11x1+
a12x2+a13x3=b1
11x1+
a12x2+a13x3=b1
a21x1+ a22x2+a23x3=b2
a31x1+ a32x2+a33x3=b3
Мұндағы аij коэффициентері мен bi босмүшелері нақты сандар болсын. Мына белгілеулерді енгізейік
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]()
Егер![]() ,
онда
Крамер
ережесі
бойынша
,
онда
Крамер
ережесі
бойынша
![]()
Мысал. Мына жжүйенің шешімін Крамер формулаларын қолданып табу керек
![]()
Шешемі.
Анықтауыштарын
есептейміз
![]() =
=![]() =290,
=290,
![]() 1=
1=![]() =580,
=580,
![]() 2=
2=![]() =-580,
=-580,
![]() 3=
3=![]() =290
=290
Сонымен,
![]() ,
яғни
(2;-2;1) үштегі
қарастырылып
отырған
теңдейлер
жүйесінің
шешімі
болады.
,
яғни
(2;-2;1) үштегі
қарастырылып
отырған
теңдейлер
жүйесінің
шешімі
болады.
Матрицалар және оларға амалдар қолдану
![]() санын
А матрицасына көбейту үшін оның әрбір
элементін сол санға көбейту қажет
санын
А матрицасына көбейту үшін оның әрбір
элементін сол санға көбейту қажет
Бірдей өлшемді А және В матрицаларының қосындысы деп өлшемі А мен В өлшеміндей, элементтері А мен В элементтерінің қосындысыны тең матрицаны атайды.
А және В матрицаларының көбейтіндісі деп сij – элементтері А матрицасының i – ші жатық жолы элементтерін В матрицасының j – ші тік жолының сәйкес элементтеріне көбейтіп қосқанға тең С матрицасын атайды.
Мысал.
Берілген
А=![]() және
В =
және
В =
![]() .
Табу
керек 2А+3В
.
Табу
керек 2А+3В
2А+3В=
2![]() +3
+3![]() =
=![]() +
+![]() =
=
=![]() =
=![]()
![]()
Мысал.
А=![]() ,
В =
,
В =
![]() Табу
керек: АВ
.
Табу
керек: АВ
.
![]()
![]() =
=![]() =
=
=![]()
Кері матрица
Анықтама. Бас диагональ элементтірінің барлығы тегіс бірге тең диагональдік матрица бірлік матрица деп аталады және былай белгілінеді:
![]()
Анықтама. Шаршы А матрицасын алайық. Егер А-1А=Е теңдігін қанағаттандыратын шаршы А-1 матрицасы табылса, онда А-1 матрицасы А матрицасына кері матрица деп аталады.
Кері
матрица мына формуламен есептеледі
А-1![]() =
=![]()
Мысал.
Берілген
А=![]() матрицасына кері матрицаны
табу керек.
матрицасына кері матрицаны
табу керек.
Шешімі.
![]() det
det![]() =6
=6![]() .
Барлық алгебралық толықтауыштарын
есептеп табамыз
.
Барлық алгебралық толықтауыштарын
есептеп табамыз
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Сөйтіп кері матрица
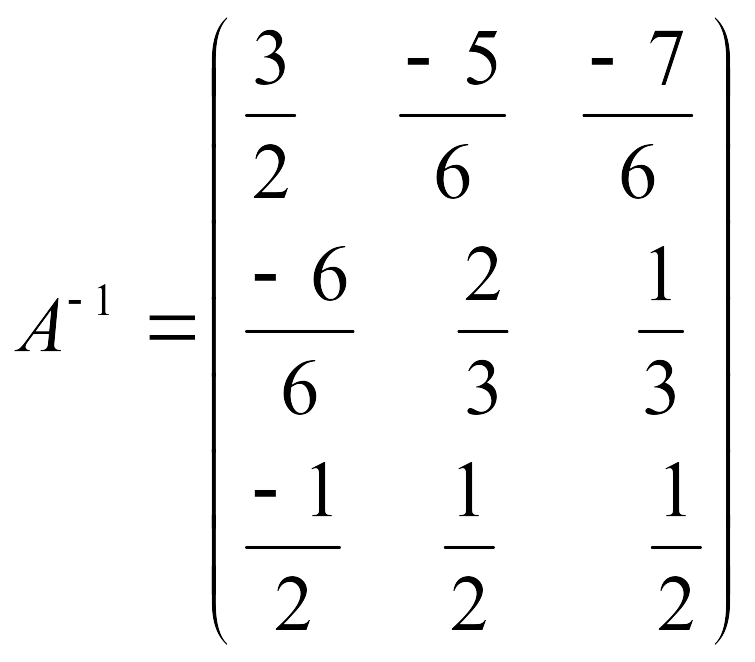
Векторлық алгебра
2 – дәріс
Векторларды анықтау. Векторды базис бойынша жіктеу
Анықтама.
Вектор
деп бағытталған кесіндіні атайды да,
![]() =
=![]() символмен белгілейді.
символмен белгілейді.
![]() ара қашықтығы
ара қашықтығы
![]()
![]() векторының ұзындығы деп аталады.
векторының ұзындығы деп аталады.
Анықтама.
![]() ,
,
![]() ,…,
,…,![]() векторларының
сызыктык комбинациясы деп мына түрдегі
векторларының
сызыктык комбинациясы деп мына түрдегі
![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]() кез
келген векторды атайды, мұндағы
кез
келген векторды атайды, мұндағы
![]() нақты
сандарын сызықтық комбинацияның
коэффициенттері деп атайды. Егер
нақты
сандарын сызықтық комбинацияның
коэффициенттері деп атайды. Егер
![]()
![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]() болса,
онда
болса,
онда
![]() векторы
векторы
![]() ,
,
![]() ,…,
,…,![]() векторлары
бойынша жіктелген дейді.
векторлары
бойынша жіктелген дейді.
Анықтама.
Бағыттары
бірдей немесе қарама – қарсы брғытталған
нөлдік емес
![]() және
және
![]() векторлары коллинеар векторлар деп
аталады да
векторлары коллинеар векторлар деп
аталады да
![]() арқылы белгілінеді. Жазықтықтағы базис
деп белгілі бір ретпен алынған осы
жазақтықтың кез келген коллинеар емес
векторлар парын атайды.
арқылы белгілінеді. Жазықтықтағы базис
деп белгілі бір ретпен алынған осы
жазақтықтың кез келген коллинеар емес
векторлар парын атайды.
Теорема.
Жазықтағы
кез келген
![]() векторын осы жазықтықтың коллинеар
емес кез келген
векторын осы жазықтықтың коллинеар
емес кез келген
![]() және
және
![]() векторлары бойынша жіктеуге болады
және ол жіктеу жалғыз ғана болады, яғни
векторлары бойынша жіктеуге болады
және ол жіктеу жалғыз ғана болады, яғни
![]() .
К1,
к2
сандары
.
К1,
к2
сандары
![]() базісі бойынша алынған
базісі бойынша алынған
![]() векторының координаталары деп аталады
да, алынған ретімен жақшаға алынып,
былай
векторының координаталары деп аталады
да, алынған ретімен жақшаға алынып,
былай
![]() жазылады.
жазылады.
Анықтама.
Егер
![]() векторлары бір жызыктыққа параллель
болса, онда оларды компланар векторлар
деп атайды.
векторлары бір жызыктыққа параллель
болса, онда оларды компланар векторлар
деп атайды.
Егер
![]() компланар болса, онда
компланар болса, онда
![]() жіктелу
орындлады.
жіктелу
орындлады.
Декарттық координаталар жүйесі. Векторларға сызықтық амалдар қолдану
Анықтама.
Егер
базис векторлары
![]() өзара перпендикуляр бірлік векторалар
болса, онда кеңістіктегі о,
өзара перпендикуляр бірлік векторалар
болса, онда кеңістіктегі о,
![]() координаталар жүйесі декарттық тік
бұрышты координаталар жүйесі дер
аталады. Декарттық тікбұрышты координаталар
жүйесінің базистік бірлік векторларын
координаталар жүйесі декарттық тік
бұрышты координаталар жүйесі дер
аталады. Декарттық тікбұрышты координаталар
жүйесінің базистік бірлік векторларын
![]() символдарымен белгілейді. Сонда
кеңістіктегі
символдарымен белгілейді. Сонда
кеңістіктегі
![]() арқылы жазылады.
арқылы жазылады.
![]() және
және
![]() векторлары
берілсін дейік.
векторлары
берілсін дейік.
Мына ережелер орындалады:
![]()
![]()
![]()
Мысал.
Берілген
![]() және
және
![]() .
Табу керек
.
Табу керек
![]() 3-дәріс
3-дәріс
Екі вектордың скаляр көбейтіндісі
Анықтама.
Екі вектордың скаляр көбейтіндісі деп
сол векторлардың модульдерін олардың
арасындағы бұрыштың косинусына
көбейтіндісін айтады, оны былайша
белгілейді:
(![]() )=
)=
![]() ,
мұндағы
,
мұндағы
![]()
![]() және
және
![]() векторларының арасындағы бурыш.
векторларының арасындағы бурыш.
Егер
![]() және
және
![]() векторлары
берілсін дейік, онда олардың скаляр
көбейтіндісі мына формуламен есептеледі
векторлары
берілсін дейік, онда олардың скаляр
көбейтіндісі мына формуламен есептеледі
(![]() )=
)=![]()
Салдар.
Егер
![]() болса , онда вектор ұзындығы сына формула
бойынша анықталады
болса , онда вектор ұзындығы сына формула
бойынша анықталады
![]()
Салдар.
Егер
![]() және
және
![]() ,
онда
,
онда
![]() және
және
![]() векторлары арасындағы бұрыш мына формула
бойынша есептеледі:
векторлары арасындағы бұрыш мына формула
бойынша есептеледі:
cos![]()
Салдар.
![]() векторының
бағыттауыш косинустары
векторының
бағыттауыш косинустары
cos![]() ,
cos
,
cos![]() ,
cos
,
cos![]()
Екі вектордың векторлық көбейтіндісі
Анықтама.
![]() және
және
![]() векторларының
векторлық көбейтіндісі деп с=
векторларының
векторлық көбейтіндісі деп с=![]() символымен белгіленген мына шартты
қанағаттындыратын
символымен белгіленген мына шартты
қанағаттындыратын
![]() векторын атайды:
векторын атайды:
![]() =
Sпар.
=
Sпар.
![]() және
және
![]()
с=![]() =
(
=
(![]() )
)
Векторларды аралас көбейтіндісі
Анықтама.
![]() векторларының аралас көбейтіндісі деп
векторларының аралас көбейтіндісі деп
![]() вектормен
вектормен
![]() векторының скалярлық көбейтіндісіне
тең санды атайды, яғни (
векторының скалярлық көбейтіндісіне
тең санды атайды, яғни (![]() )=(
)=(![]() )
)![]() .
.
1.
Егер
![]() ,
,
![]() ,
,
![]() ,
онда олардың аралас көбейтіндісі үшінші
ретті анықтауышқа тең, яғни
,
онда олардың аралас көбейтіндісі үшінші
ретті анықтауышқа тең, яғни
(![]() )=
)=![]()
2.
![]() векторлары компланар векторлар болуы
үшін, олардың аралас көбейтіндісі нөлге
тең болуы қажетті жуне жеткілікті, яғни
(
векторлары компланар векторлар болуы
үшін, олардың аралас көбейтіндісі нөлге
тең болуы қажетті жуне жеткілікті, яғни
(![]() )=0.
)=0.
3.
Компланар
емес
![]() векторларының аралас көбейтіндісі
модуль бойынша сол үш векторларға
салынған параллелепипедтің көлеміне
тең болады, яғни V=
векторларының аралас көбейтіндісі
модуль бойынша сол үш векторларға
салынған параллелепипедтің көлеміне
тең болады, яғни V=![]() .
.
Векторлардың перпендикулярлық және коллинеарлық шарттары
1.
Егер
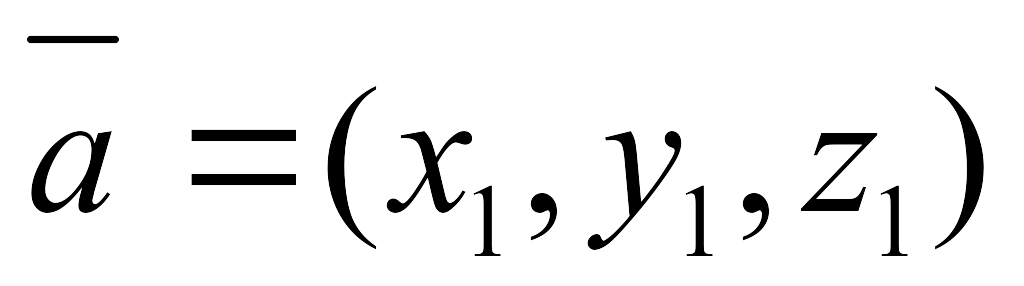 және
және
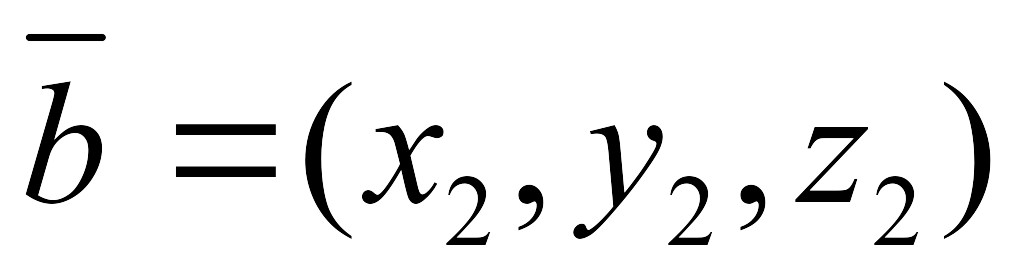 векторлары коллинеар болса, онда олардың
сәйкес координаталары пропорционал
болады, яғни
векторлары коллинеар болса, онда олардың
сәйкес координаталары пропорционал
болады, яғни
![]()
2.
![]() және
және
![]() векторлары
перпендикуляр болуы үшін
векторлары
перпендикуляр болуы үшін
![]() теңдігі
орындалады.
теңдігі
орындалады.
4-дәріс.
Жазықтықтағы аффиндік және тік бұрышты координаталар жүйесі. Түзудегі, жазықтықтағы және кеңістіктегі тік бұрышты координаталар жүйесі. Кесіндіні берілген қатынаста бөлу
Жазықтықтағы аналитикалық геометрия
Жазықтықтағы түзүдің теңдеулері
Анықтама.
Ах+Ву+С=0
теңдеу
түзудің
жалпы
теңдеуі
деп
аталады.
Бұдан
![]() .
Мұндағы
к=
.
Мұндағы
к=![]() - түзудің
бұрыштық
коэффициенты.
- түзудің
бұрыштық
коэффициенты.
-
Бағыттауыш векторы
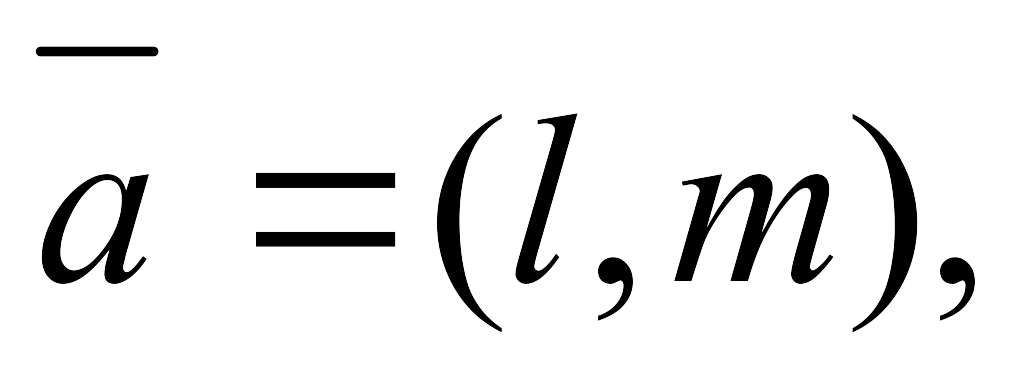 (түзуге
параллель),
М0(x0,y0)
нүктесі
арқылы
өтетін
түзудің
теңдеуі
(түзуге
параллель),
М0(x0,y0)
нүктесі
арқылы
өтетін
түзудің
теңдеуі
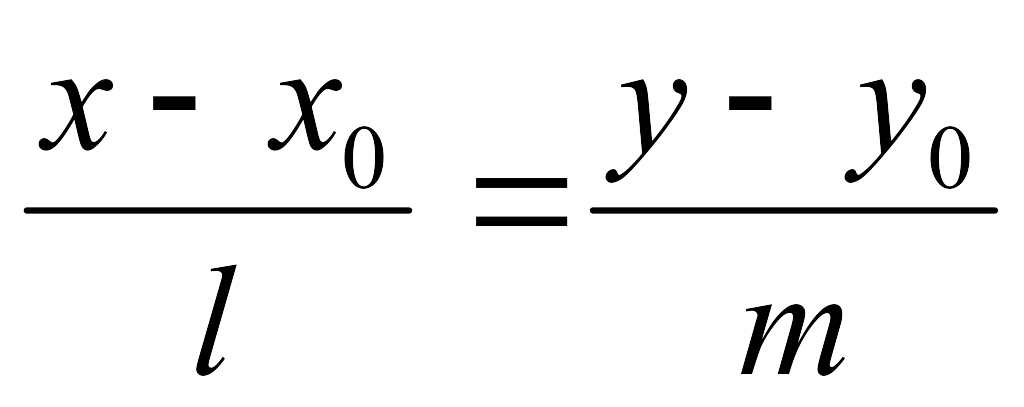 болады.
Бұл теңдеуді қорытып шығару үшін
берілген түзудің бойынан тағы бір М(х,
у) нүкте аламыз. Сонда
болады.
Бұл теңдеуді қорытып шығару үшін
берілген түзудің бойынан тағы бір М(х,
у) нүкте аламыз. Сонда
 векторы
векторы
 векторына коллинеар. Демек, олардың
сәйкес координаталары пропорционал,
яғни
векторына коллинеар. Демек, олардың
сәйкес координаталары пропорционал,
яғни
 .
. -
Нормаль векторына
 перпендикуляр
болып,
М0(x0,y0)
нүктесі арқылы өтетін түзудің теңдеуі
A(x-x0)+B(y-y0)=0.
Бұл
теңдеуді қорытып шығару үшін берілген
түзудің бойынан тағы бір М(х, у) нүкте
аламыз. Сонда
перпендикуляр
болып,
М0(x0,y0)
нүктесі арқылы өтетін түзудің теңдеуі
A(x-x0)+B(y-y0)=0.
Бұл
теңдеуді қорытып шығару үшін берілген
түзудің бойынан тағы бір М(х, у) нүкте
аламыз. Сонда
 векторы
векторы
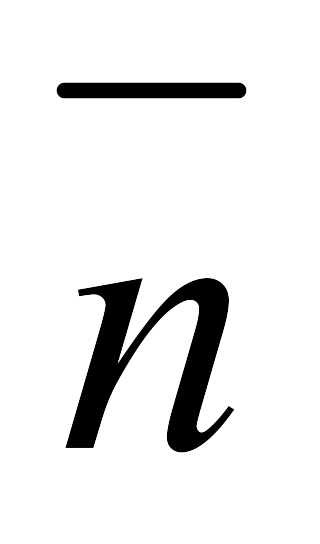 векторына перпендикуляр болады, яғни
олардың скаляр көбейтіндісі нөлге тең.
Сонда мына теңдік A(x-x0)+B(y-y0)=0
шығады. Бұл ізделінді түзудің теңдеуі.
векторына перпендикуляр болады, яғни
олардың скаляр көбейтіндісі нөлге тең.
Сонда мына теңдік A(x-x0)+B(y-y0)=0
шығады. Бұл ізделінді түзудің теңдеуі. -
Бұрыштық коэффициенті к болып, М0(x0,y0) нүкте арқылы өтетін түзудің теңдеуі y-y0=k(x-x0). Мұны қорыту үшін түзудің у=кх+в (1) теңдеуін алайық. М0 нүкте түзу бойында жақандықтан, оның координаталары (1) теңдеуді қанағаттандырады, яғни у0 =кх0 +в (2) теңдігі орындалады. (1) теңдіктен (2) теңдікті шегерсек, y-y0=k(x-x0) теңдігі шығады. Бұл бұрыштық коэффициенті к болып, М0(x0,y0) нүктесі арқылы өтетін түзудің теңдеуі.
-
Берілген екі нүкте М1(x1,y1) және М2(x2,y2) нүктелері өтетін түзудің теңдеуі
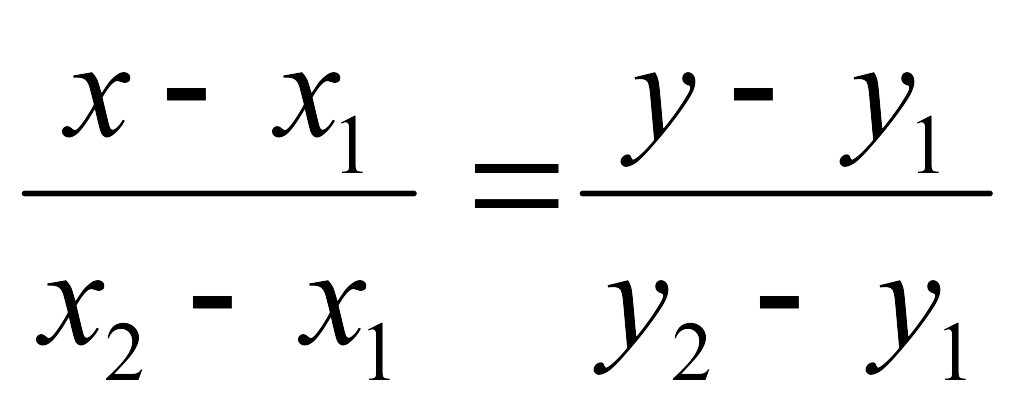 . Мұнда түзу бойынан кез келген бір М
(х, у) нүкте аламыз. М1
нүктені М және М2
нүктелерімен қоссақ,
. Мұнда түзу бойынан кез келген бір М
(х, у) нүкте аламыз. М1
нүктені М және М2
нүктелерімен қоссақ,
 =(х
– х1
, у
– у1),
=(х
– х1
, у
– у1),
 =(х2
– х1
,
у2
– у1),
векторлары коллинеар болады. Бұдан
=(х2
– х1
,
у2
– у1),
векторлары коллинеар болады. Бұдан
 ізделінді теңдеу шығады.
ізделінді теңдеу шығады.
Координаталар
өстерін А(a,0), B(0,b) нүктелерінде қиып
өтетін түзудің теңдеуі
![]() (Студенттердің өз беттерімен қорытуына
беріледі).
(Студенттердің өз беттерімен қорытуына
беріледі).
Екі түзу арасындағы бұрыш. Параллельдік және перпендикулярлық шарттары. Нүктеден түзуге дейінгі қашықтығы
d1 және d2 түзулері өздерінің сәйкес жалпы теңдеулері арқылы берілсін дейік:
А1х+В1у+С=0, А2х+В2у+С=0
Бұрыштық
коэффициенттері к1=![]() ,
к2=
,
к2=![]()
Егер d1 d2, онда к1 = к2.
Егер
d1
![]() d2,
онда к1
=
d2,
онда к1
=![]() .
.
Екі
түзу арасындағы бұаыш tg![]() (Студенттердің өз беттерімен қорытуына
беріледі)..
(Студенттердің өз беттерімен қорытуына
беріледі)..
M(x0,y0)
нүктеден түзуге дейінгі қашықтығы d=
![]() (Студенттердің өз беттерімен қорытуына
беріледі).
(Студенттердің өз беттерімен қорытуына
беріледі).
 у
у

М
 r1
r1
r2
![]() F1
O
F2
F1
O
F2
![]()
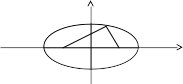
F1, F2 – эллипстің фокустары. F1 = (-c; 0); F2(c; 0), F1F2 = 2c.
с – фокустары ар қашықтығының жартысы; 2а - тұрақты шама. F1М және F2М қашықтықтарын r1= F1М, r2= F2М деп белгілесек, онда (2) теңдік мына түрде жазылады:
r1 + r2 = 2а (21)
Екі
нүктені ара қашықтығының формуласы
бойынша:
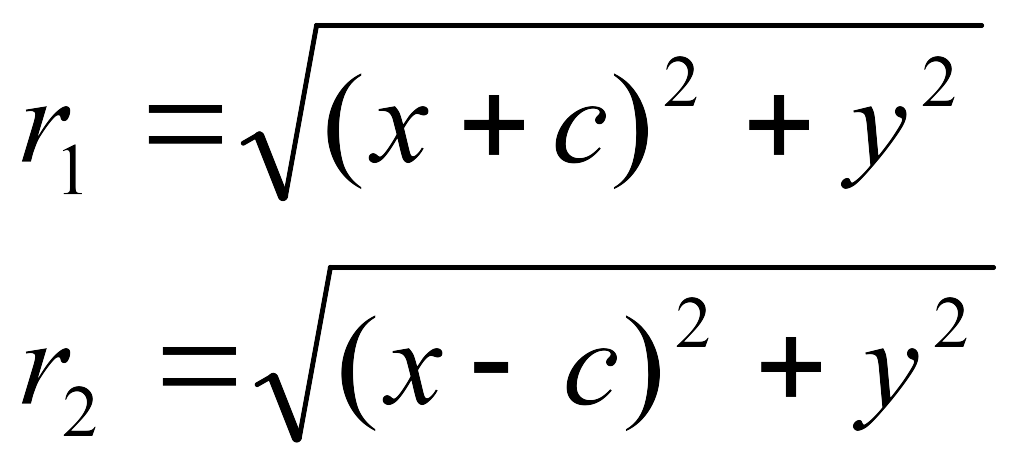
![]() .
.
Бұл теңдеуді түрлендіріп, эллипстің жабайы (канондық) теңдеуін табайық:
![]()
![]()
х
2+2сх+с2+
у2
= 4а2
– 4а![]()
а![]() теңдіктің
екі жағын а
- ға
бөліп, квадраттайық:
теңдіктің
екі жағын а
- ға
бөліп, квадраттайық:
х2
-2сх+с2+у2
= (а -
![]()
х2
-2сх+с2+у2
=![]()
а2х2+а2у2+а2с2= а4 + с2х2,
(а2- с2) х2+а2у2+ = а2 ( а2 - с2),

а с болғандықтан, а2 - с2 0 болады, сондықтан а2 - с2 в2 (3) деп белгілейміз.

Сонда
в2
х2+а2у2+
= а2
в2
шығады,
осыдан
![]() (4), мұндағы х
пен
у
-
(4), мұндағы х
пен
у
-
эллипстің бойындағы кез келген нүктелердің координаталары, а – эллипстің үлкен жарты өсі, в – оның кіші жарты өсі. (4) теңдеу эллипстің жабайы (канондық) теңдеуі деп аталады.
Теорема. Эллипстің фокустық ара қашықтығы мен жарты өстері мынадай қатынас бойынша байланысады:
a2 = b2 + c2.
Дэлелдеу:
Егер
М нүкте
эллипстің
вертикаль осьпен
қиылысу нүктесінде болса,
онда
r1
+ r2
= 2![]() (
Пифагор теоремасы
бойынша).
Егер
М нүкте
эллипстің
горизонталь
осьпен
қиылысу нүктесінде болса,
онда r1
+ r2
= a
– c
+ a
+ c.
Эллипстің
(
Пифагор теоремасы
бойынша).
Егер
М нүкте
эллипстің
горизонталь
осьпен
қиылысу нүктесінде болса,
онда r1
+ r2
= a
– c
+ a
+ c.
Эллипстің
нықтамасы бойынша r1 + r2 – қосынды тұрақты шама, ендеше жоғарыдағы екі теңдікті теңестіріп, мынадай теңдік аламыз:
a 2
= b2
+ c2
.
2
= b2
+ c2
.

Анықтама.
![]() = с/a
қатынас эллипстің эксцентриситеті
деп аталады.
с < a
= с/a
қатынас эллипстің эксцентриситеті
деп аталады.
с < a
болғандықтан,
![]() < 1 болады.
< 1 болады.
Эллипстің түрін оның жабайы теңдеуі бойынша зерттеу.
(4)
теңдеу бойынша эллипстің бірнеше
қасиеттерін анықтайық.. х=а х=-а
у у=в М М2 В2

х А1 А2 О






у=-в М1 М3 В1

Координата басына қарағанда симметриялы .
2)
у=0 болса,
![]() болады, бұдан х =
а.
Сондықтан эллипс ох осін А1(-а;
0) және А2(а;0)
нүктелерінде қияды. Ал х=0
болғанда
болады, бұдан х =
а.
Сондықтан эллипс ох осін А1(-а;
0) және А2(а;0)
нүктелерінде қияды. Ал х=0
болғанда
![]() шығады да, у=
в.
Демек, эллипс оу осін В1(0;-в),
В2(0;
в) нүктелерінде қияды. Эллипстің осьтермен
қиылысу нүктелері (А1,
А2,
В1,
В2
) төбелері
деп аталады.
шығады да, у=
в.
Демек, эллипс оу осін В1(0;-в),
В2(0;
в) нүктелерінде қияды. Эллипстің осьтермен
қиылысу нүктелері (А1,
А2,
В1,
В2
) төбелері
деп аталады.
