МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра проектирования технологических машин



Расчетно-графическая работа по дисциплине:
«Прикладная механика»

Работу выполнил:

Власовец Игорь Дмитриевич

Группа: ЗФ-808 Oценка:___________________

_________________________

Шифр: 133144606 _________________________

Дата:
Преподаватель: Чусовитин Николай Анатольевич
Подпись:

Новосибирск 2021

Задача № 4

Для заданного стального бруса (рис. 4.1) требуется:

1) построить эпюры продольных сил , нормальных напряжений и перемещений ;

2) если зазор перекрывается, то раскрыть статическую неопределимость и построить эпюры продольных сил , нормальных напряжений и перемещений ;

3) если зазор не перекрывается, то определить усилие, которое необходимо приложить к сечению, чтобы зазор закрылся. Построить эпюры продольных сил , нормальных напряжений и перемещений ;

4) провести анализ и сделать заключение о влиянии зазора на распределение напряжения по сечению брусьев.

Принять: допускаемое напряжение – , модуль упругости - . Исходные данные:

---

; . Длины участков: ; ; . Площади поперечных сечений: ; ; . Зазор .



Рис. 4.1. Брус.

Решение:

1. Находим продольные силы , нормальные напряжения и перемещения для статически определимого бруса. Для этого отбрасываем заделку правее зазора. Разбиваем брус на три силовых участка. Границами силовых участков являются: сечения приложения сосредоточенных нагрузок, сечения изменения профиля бруса, концевые сечения бруса. Порядок отсчета ведем от свободного конца бруса.



Рис. 4.2. Эпюры , , без учета зазора.

Для каждого силового участка находим закон изменения внутреннего силового фактора. Для этого берем произвольное сечение на расстоянии от границы силового участка и отбрасываем всю балку левее этого сечения, заменяя её действие силой реакции связи. За положительное направление силы реакции принимаем направление от сечения. Составляя уравнение статики, и решая его, находим значение внутреннего силового фактора.

---

На первом участке внешние силы отсутствуют и, очевидно, .

Для второго участка: , отсюда: .

Для третьего участка: , отсюда: .

По полученным значениям строим эпюру (рис. 4.2, б).

Находим напряжения на каждом силовом участке.

;

;

.

Так как на каждом силовом участке внутренне усилие – величина постоянная, площадь постоянная, то и эпюра напряжений на каждом силовом участке ограничена прямой, параллельной нулевой линии (рис. 4.2, в).

Построение эпюры перемещений начинаем с левого конца бруса, который жестко защемлён, и, следовательно, перемещение его равно нулю. Построение эпюры перемещений ведем слева направо.

В произвольном сечении третьего силового участка на расстоянии от заделки абсолютное удлинение равно:

,

где ; - модуль упругости первого рода.

Как видно из формулы, меняется по линейному закону, и для построения эпюры на силовом участке достаточно найти две точки на границах силового участка. При ; .


При ;

---

.

На втором силовом участке в произвольном сечении абсолютное удлинение будет равно алгебраической сумме перемещений третьего участка и удлинения, приобретенного на втором участке за счет внутреннего усилия , т.е.



или

, где .

Подставляя соответствующие значения величин, получим при и при

.

На первом силовом участке так как , следовательно:

.

По полученным данным строим эпюру перемещений (рис. 4.2, г).

Таким образом, из построенных эпюр видно, что при заданной геометрии бруса и под действием приложенных нагрузок крайнее правое сечение переместилось бы на 4,744 мм, если бы не было отброшенной правой заделки, а на третьем силовом участке возникли бы напряжения больше допускаемых, что может привести к разрушению бруса.

Выше было указано, что под действием приложенных нагрузок зазор перекрывается и схема примет вид, показанный на рис. 4.3.



Рис. 4.3. Брус с перекрытым зазором.

Проведем исследование равновесия для такой схемы бруса:

.

2. Для построения эпюр внутренних усилий необходимо определить реакции связей. Освобождаем брус от связей и заменяем их действие реакциями

---

и (рис. 4.3). Для такой системы сил статика дает одно уравнение. В этом уравнении два неизвестных и , следовательно, задача один раз статически неопределима.

Чтобы раскрыть статическую неопределимость, воспользуемся методом деформаций. Итак, если бы не было правой заделки, то правый свободный конец бруса переместился бы на величину , которая больше величины зазора. Однако как только зазор будет перекрыт, со стороны заделки на брус начнет действовать усилие , которое деформирует балку и «возвращает» крайнее правое сечение бруса до границы заделки (рис. 4.4).



Рис. 4.4. Схема деформаций.

Из картины деформаций видно, что . Это и есть второе уравнение, необходимое для раскрытия статической неопределимости. Учитывая, уже определено, а получим:

.

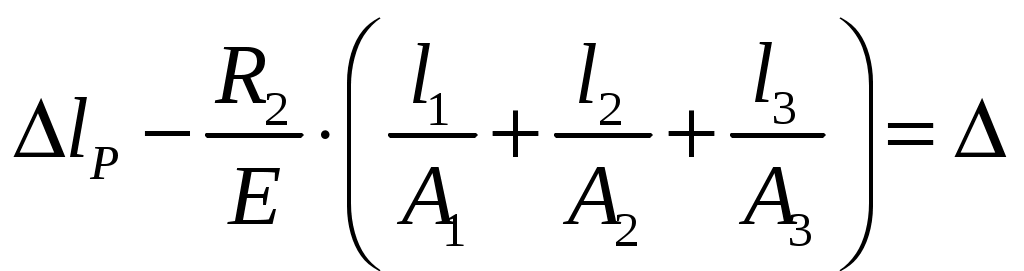Решая относительно , находим:

.

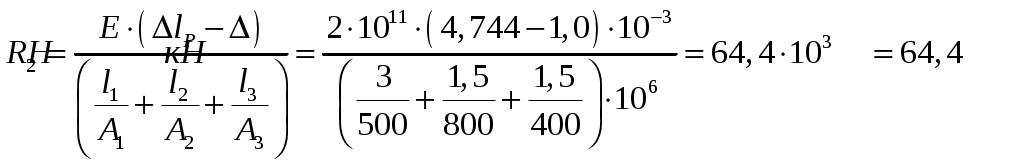Разбиваем брус на четыре силовых участка и находим продольные силы на каждом участке. Отсчет начинаем с правого конца бруса.

Для первого участка: , отсюда .

Для второго участка: , отсюда:

---

Смотрите также файлы

• Реакция гемолиза.docx

• Выделение коллекторов. Оценка характера насыщения.docx

• Техническая характеристика на приобретение, установку, монтаж, демонтаж и наладка антивандального шлагбаума в комплекте на гидротехнических сооружениях, гидроузел Аклак..docx

• .doc

• Студент Физика Химия.docx