Файл: Расчетнографическая работа по дисциплине Прикладная механика Работу.doc
Добавлен: 07.11.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Для третьего участка: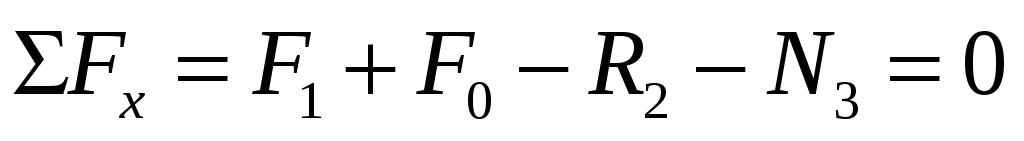 , отсюда:
, отсюда:
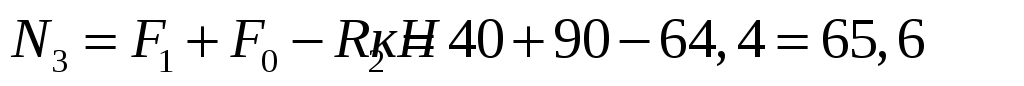 .
.
По полученным значениям строим эпюру (рис. 4.5, б).
(рис. 4.5, б).
Находим напряжения на каждом силовом участке.
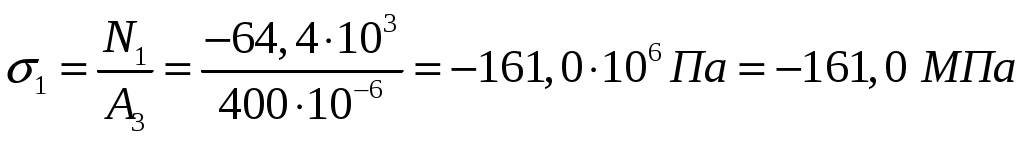 ;
;
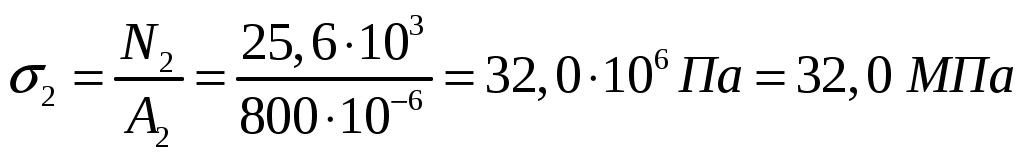 ;
;
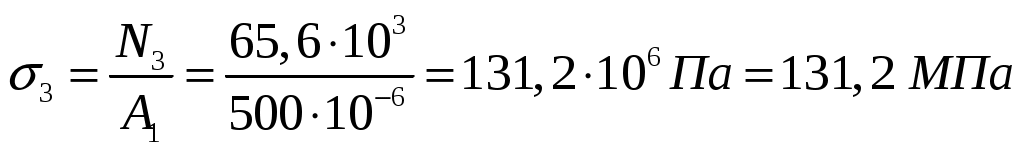 .
.
По полученным значениям строим эпюру (рис. 4.5, в).
(рис. 4.5, в).
Построение эпюры перемещений начинаем с левого конца бруса, который жестко защемлён, и, следовательно, перемещение его равно нулю. Построение эпюры перемещений ведем слева направо.
Для третьего силового участка на расстоянии от заделки абсолютное удлинение равно:
от заделки абсолютное удлинение равно:
 , где
, где  .
.
При ;
;  .
.
При ;
; 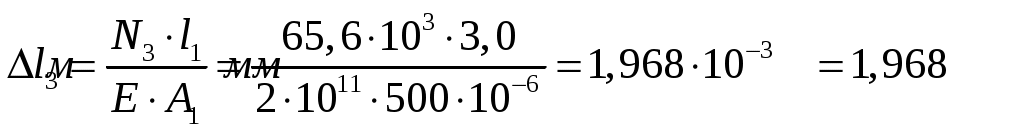 .
.
Для второго силового участка абсолютное удлинение равно:
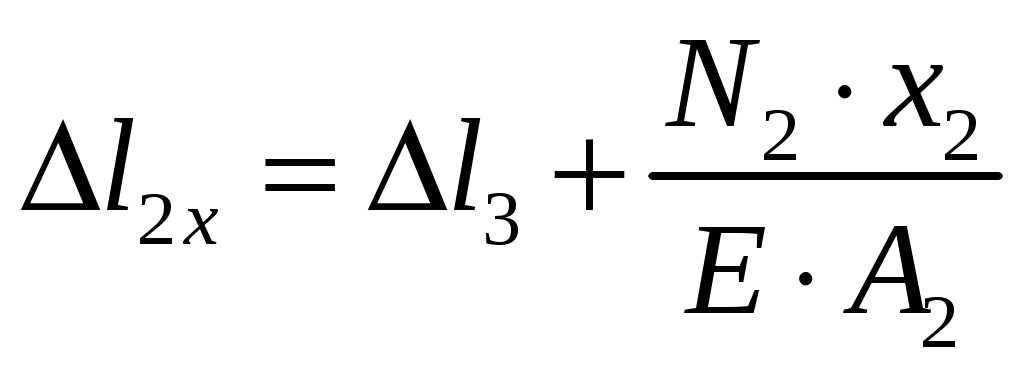 , где
, где  .
.
При ;
; 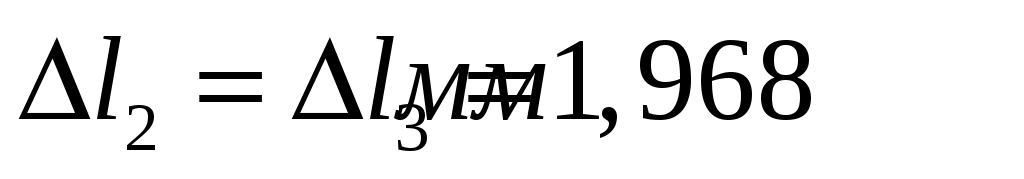 .
.
При ;
;
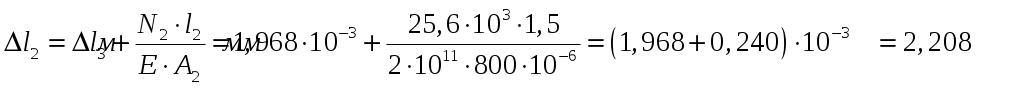 .
.
Для первого силового участка абсолютное удлинение равно:
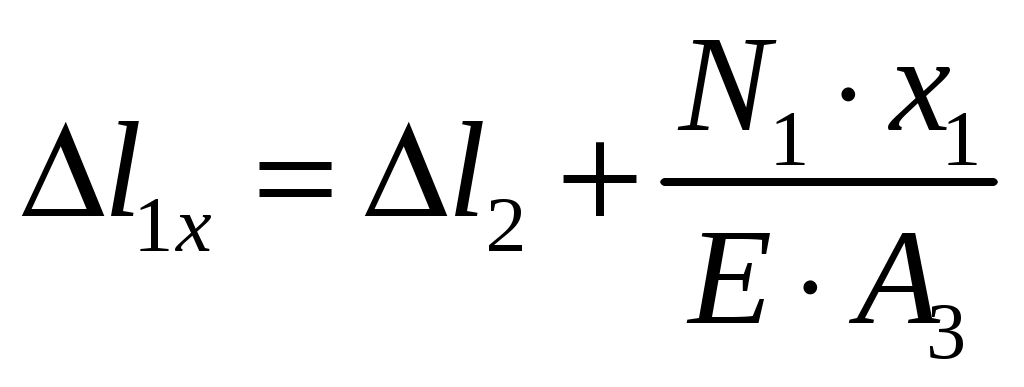 , где
, где
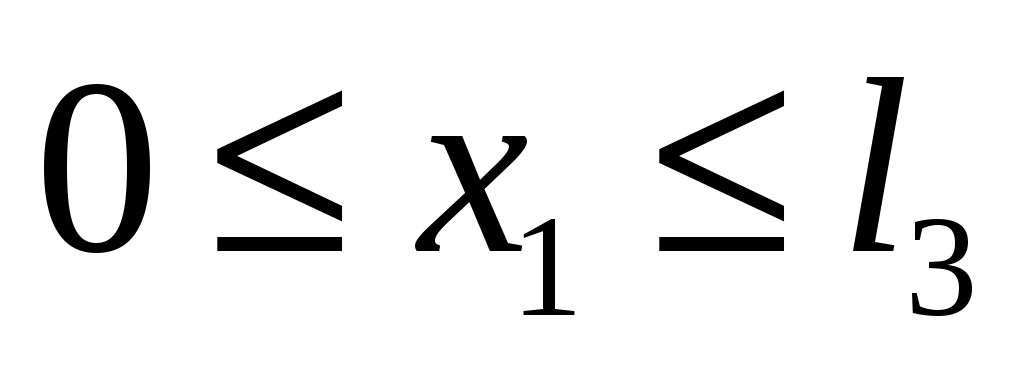 .
.
При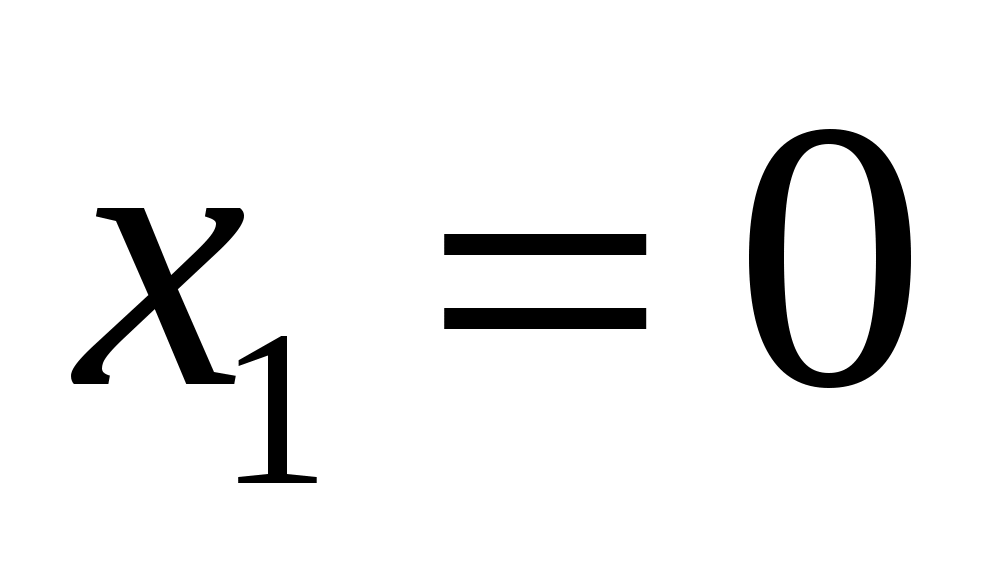 ;
; 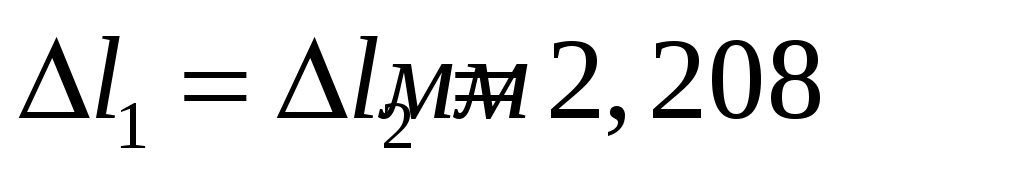 .
.
При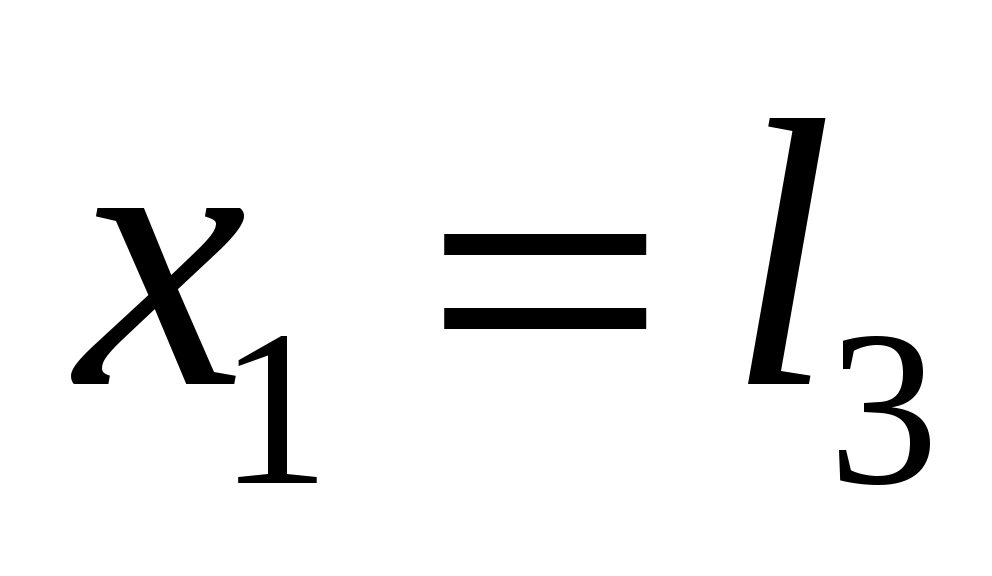 ;
;
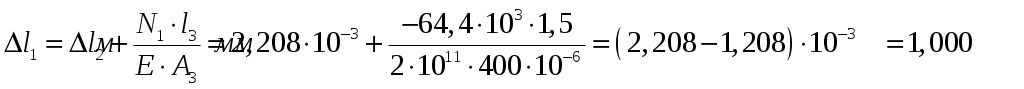 .
.
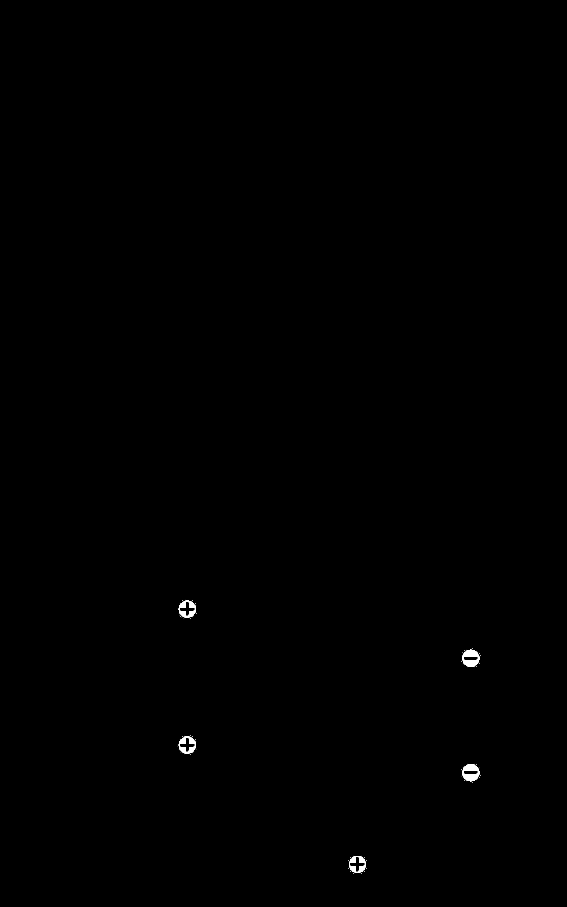
Рис. 4.5. Эпюры ,
,  ,
,  с учетом зазора.
с учетом зазора.
То есть перемещение левого конца бруса равно величине зазора. По полученным значениям строим эпюру (рис. 4.5, г).
(рис. 4.5, г).
3. Анализируя полученные результаты, видим, наличие правой заделки при существующем зазоре в 1,0 мм дало возможность понизить рабочее напряжение на третьем участке, и перераспределить его на другие участки. Таким образом, меняя величину зазора, можно регулировать и значение внутренних усилий, возникающих в сечениях бруса под действием приложенных нагрузок.
Правильность решения задачи можно проверить по эпюре деформаций. Равенство перемещения правого сечения бруса величине зазора говорит об этом.
Задача № 7
На стальной ступенчатый брус круглого поперечного сечения, закрепленного с двух сторон, действуют скручивающие моменты сил.
1. Определить диаметры стержня из условия прочности и условия жесткости.
2. Построить эпюры крутящих моментов и абсолютных углов закручивания при принятых диаметрах ступеней стержня.
3. Определить рабочие максимальные касательные напряжения и сравнить с допускаемыми касательными напряжениями.
4. Определить действительный относительный угол закручивания и сравнить с допускаемым относительным углом закручивания.
Исходные данные: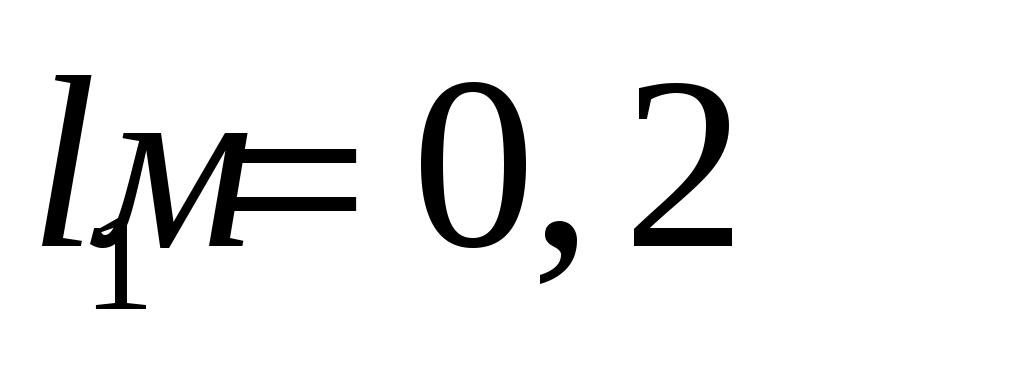 ;
; 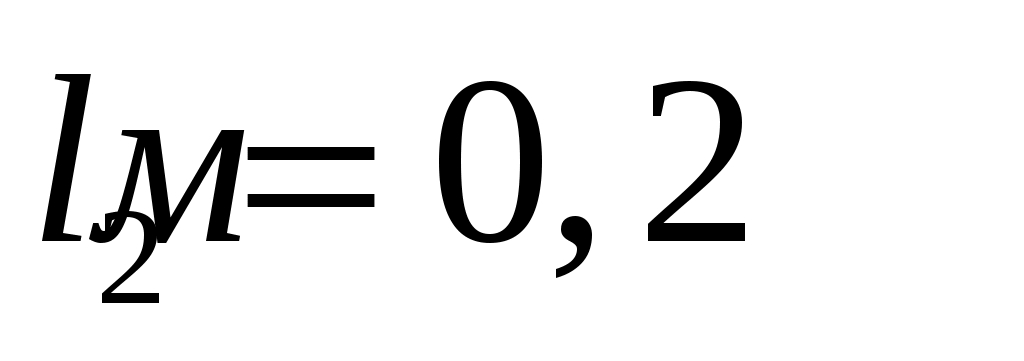 ;
; 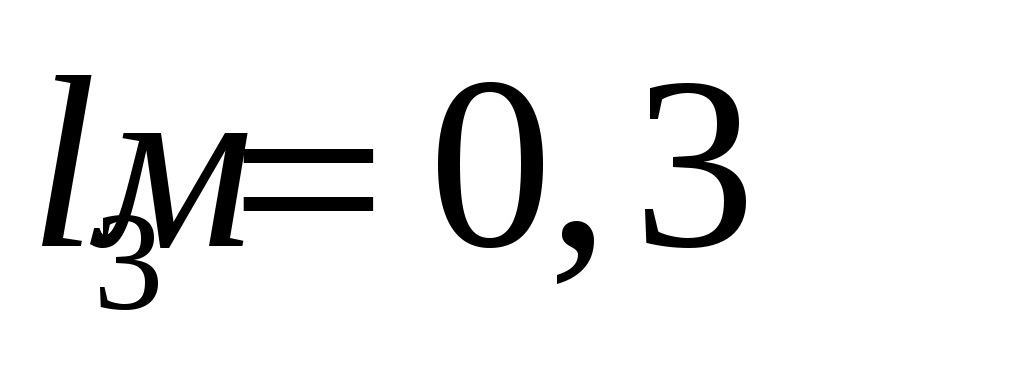
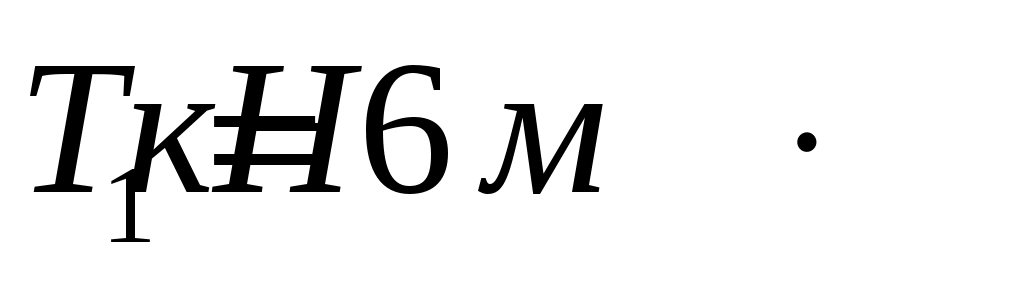
;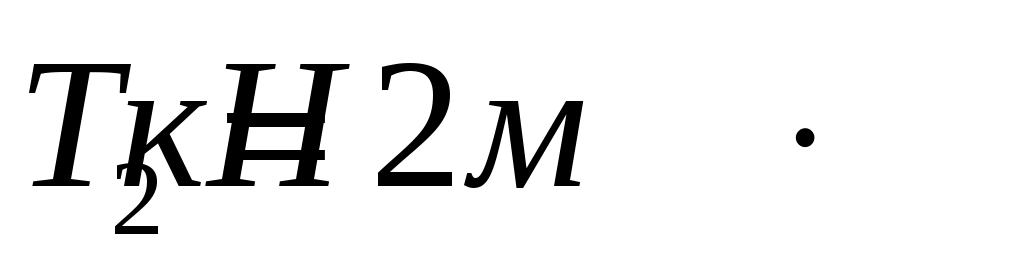 . Соотношение диаметров:
. Соотношение диаметров: 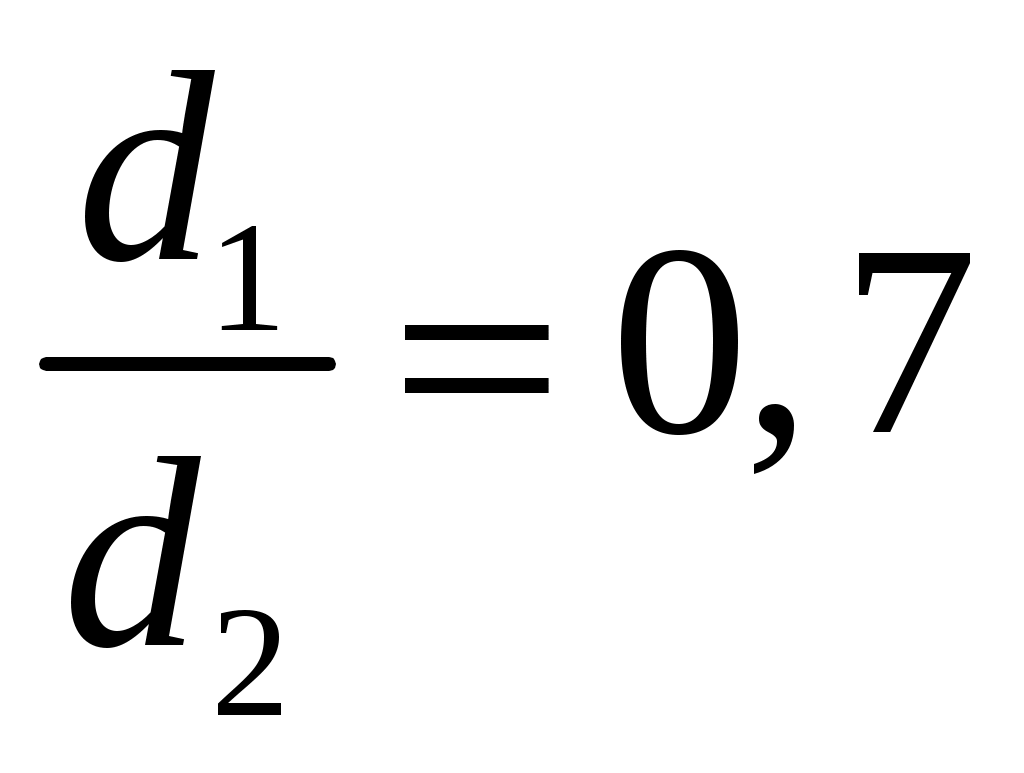 .
. 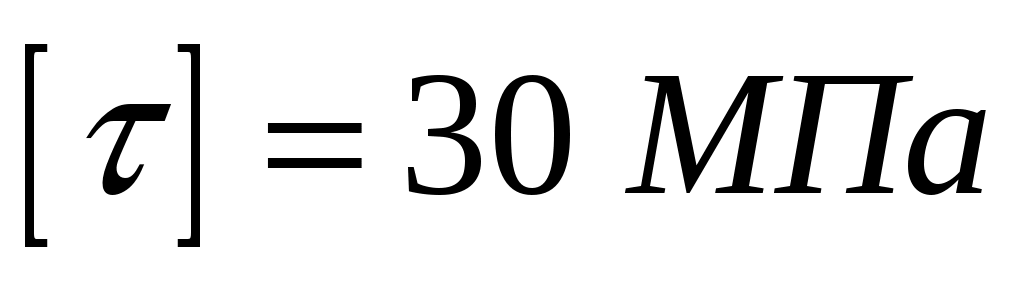 ;
; 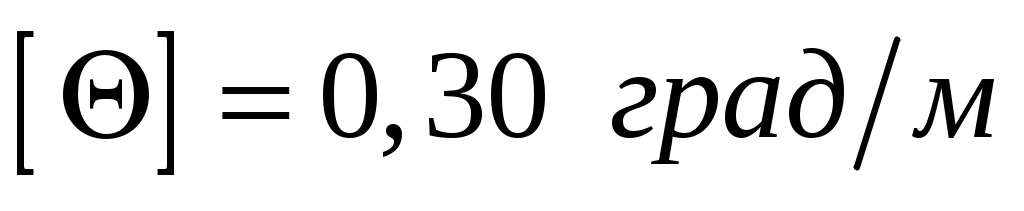 .
.
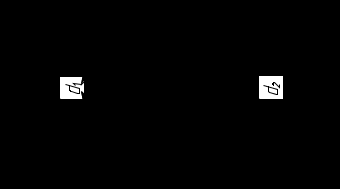
Рис. 7.1. Исходная схема.
Решение:
1. Освобождаем стержень от связей, которыми являются заделки с двух сторон, и заменяем действие связей силами реакций. Учитывая, что стержень невесомый и на него действуют только скручивающие моменты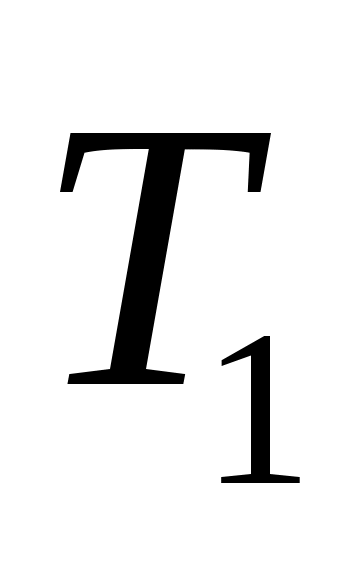 ,
, 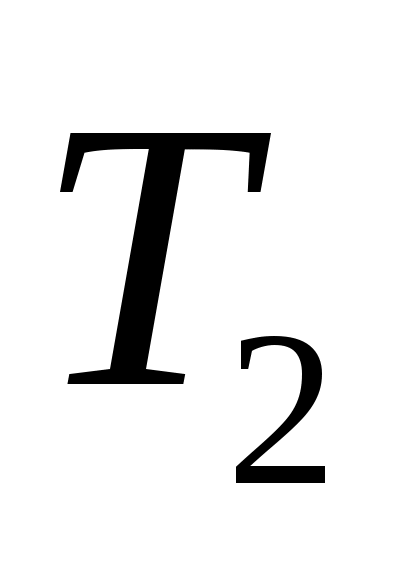 , заключаем, что в заделках возникают крутящие моменты
, заключаем, что в заделках возникают крутящие моменты 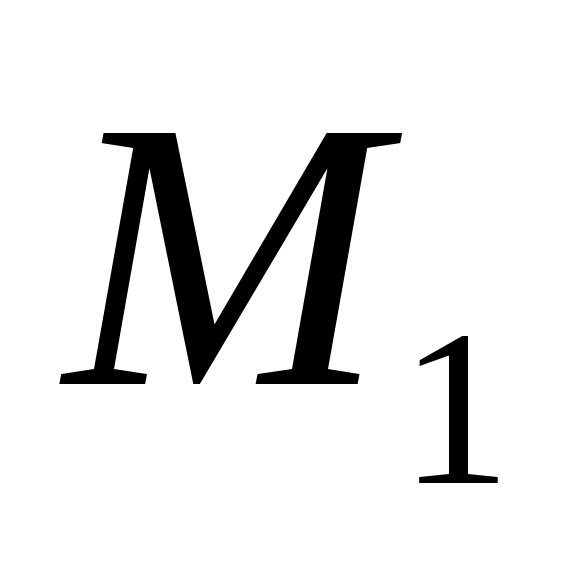 ,
, 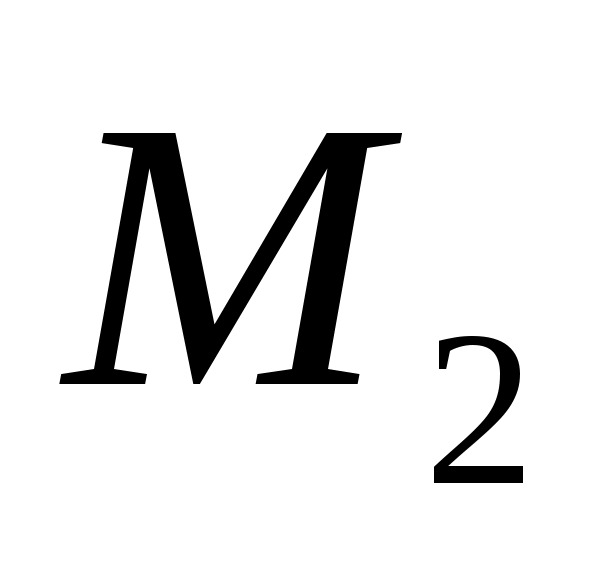 . Полученная схема стержня представлена на рис. 7.2.
. Полученная схема стержня представлена на рис. 7.2.
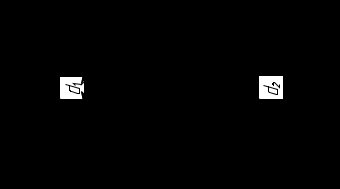
Рис. 7.2. Расчетная схема.
Для определения неизвестных моментов связей составляем уравнение статики. Для такой системы сил статика позволяет записать только одно уравнение равновесия:
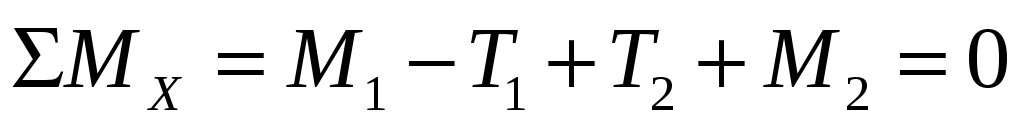 .
.
Проводя анализ, видим, что при одном уравнение статики имеем два неизвестных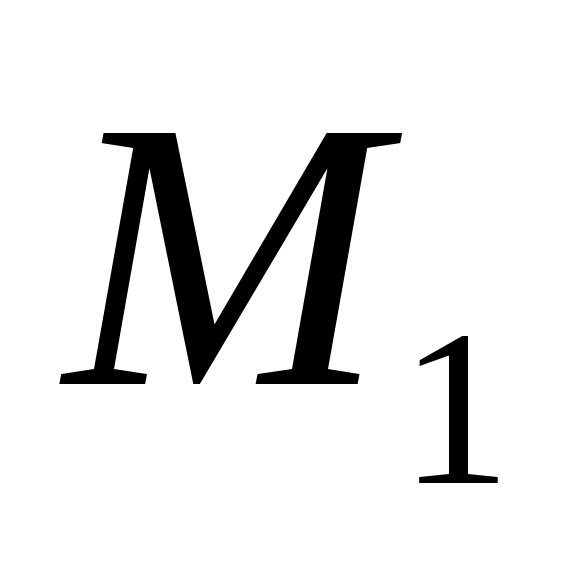 ,
, 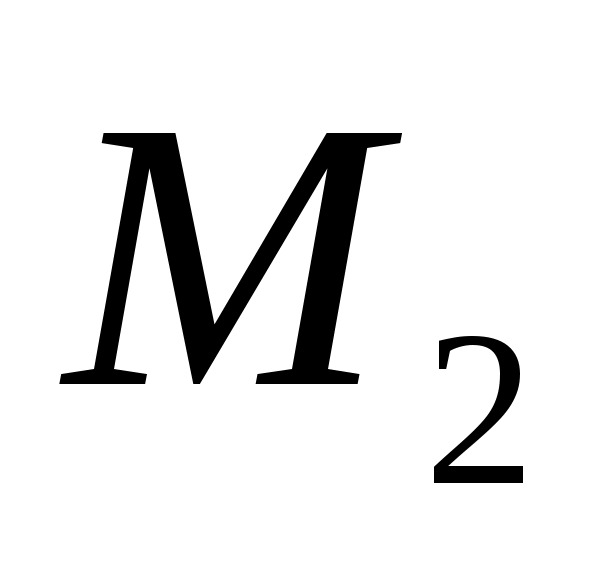 , следовательно, задача является статически неопределимой.
, следовательно, задача является статически неопределимой.
Для раскрытия статической неопределимости воспользуемся методом деформации применительно к кручению. Освободим, например, только правую заделку стального ступенчатого бруса и заменим её действие моментом связи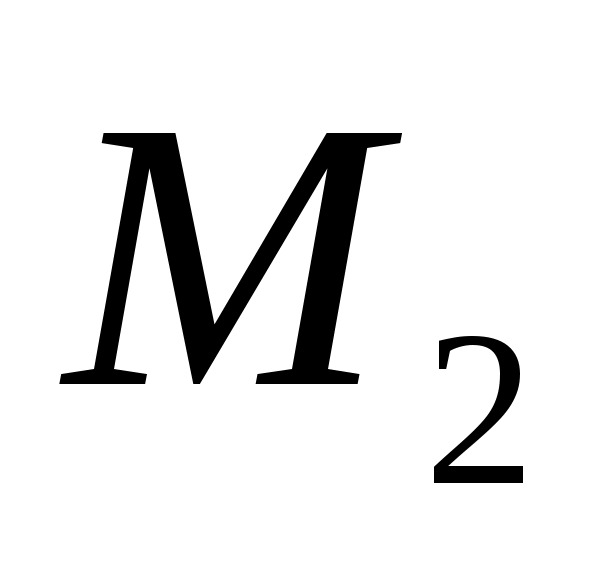 . Проведем в сечении какой-либо радиус
. Проведем в сечении какой-либо радиус 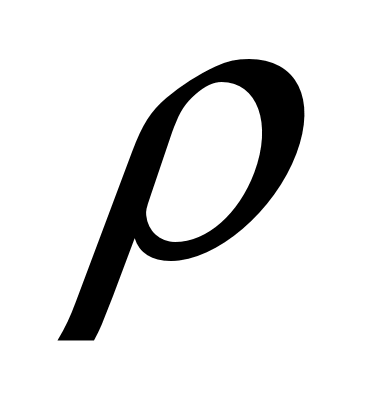 (рис. 7.3). Применим принцип независимости действия сил. Тогда под действием скручивающих моментов
(рис. 7.3). Применим принцип независимости действия сил. Тогда под действием скручивающих моментов 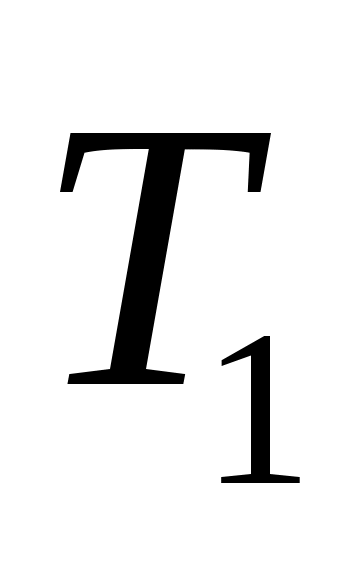 и
и 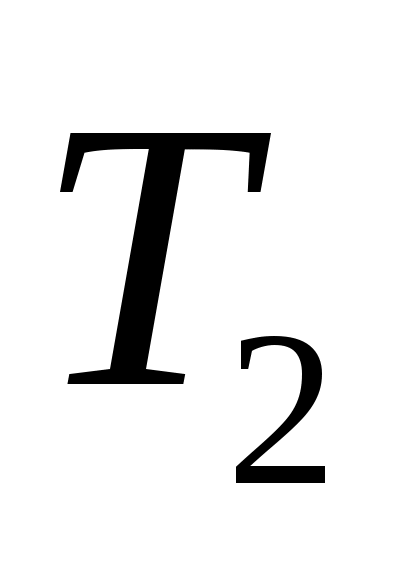
радиус повернется на какой-то угол
повернется на какой-то угол 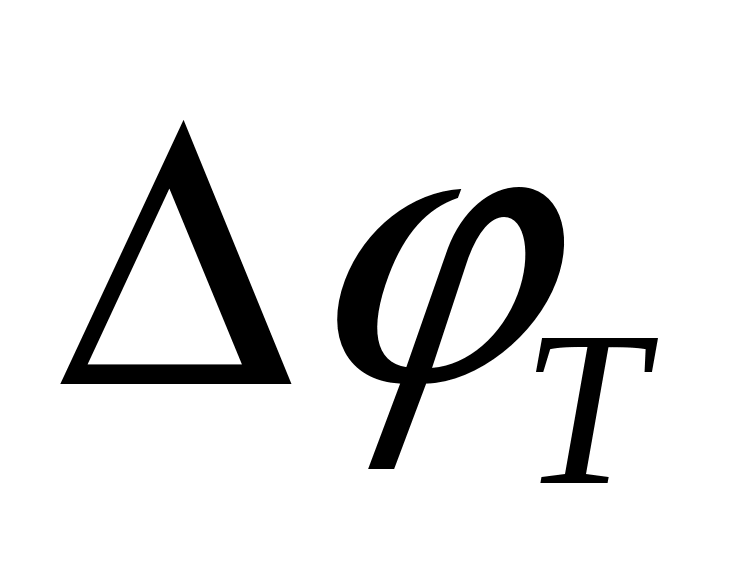 , а под действие реактивного момента
, а под действие реактивного момента  этот же радиус повернется на угол
этот же радиус повернется на угол  . Но так как в действительности сечение неподвижно, то очевидно, алгебраическая сумма этих перемещений равна нулю, т.е.
. Но так как в действительности сечение неподвижно, то очевидно, алгебраическая сумма этих перемещений равна нулю, т.е.
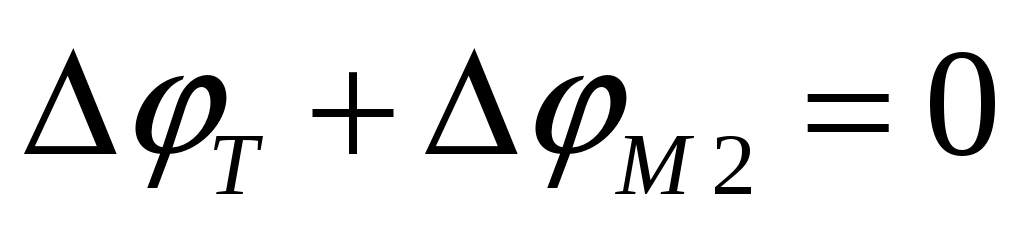 .
.

Рис. 7.3.
Это и будет являться уравнением деформации при кручении и вторым уравнением, необходимым для раскрытия статической неопределимости.
Найдем абсолютные углы закручивания:
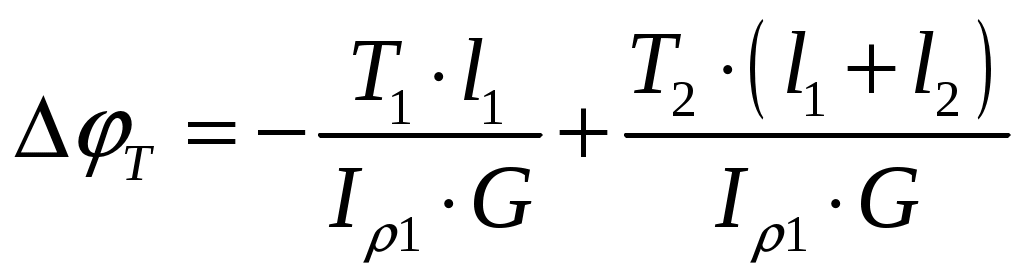 ,
,
где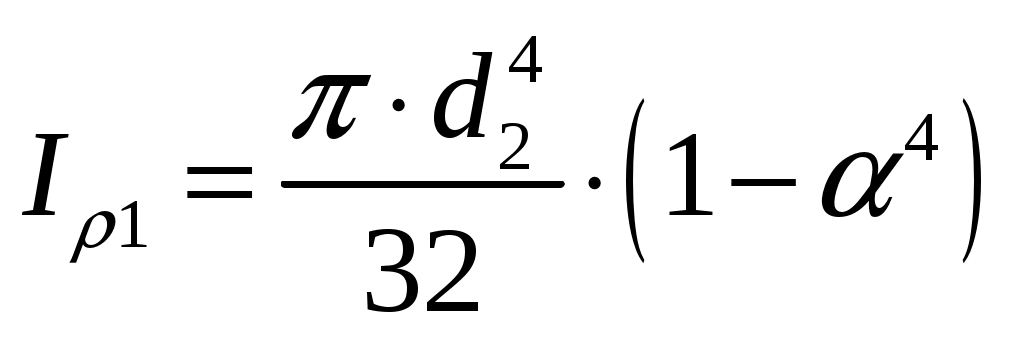 - полярный момент инерции кольцевого сечения вала на участках длиной
- полярный момент инерции кольцевого сечения вала на участках длиной 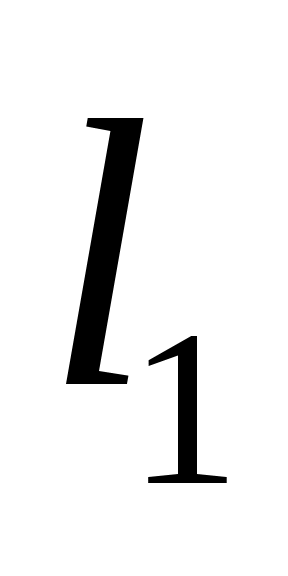 и
и 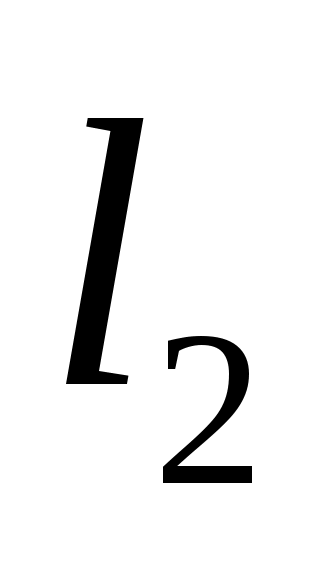
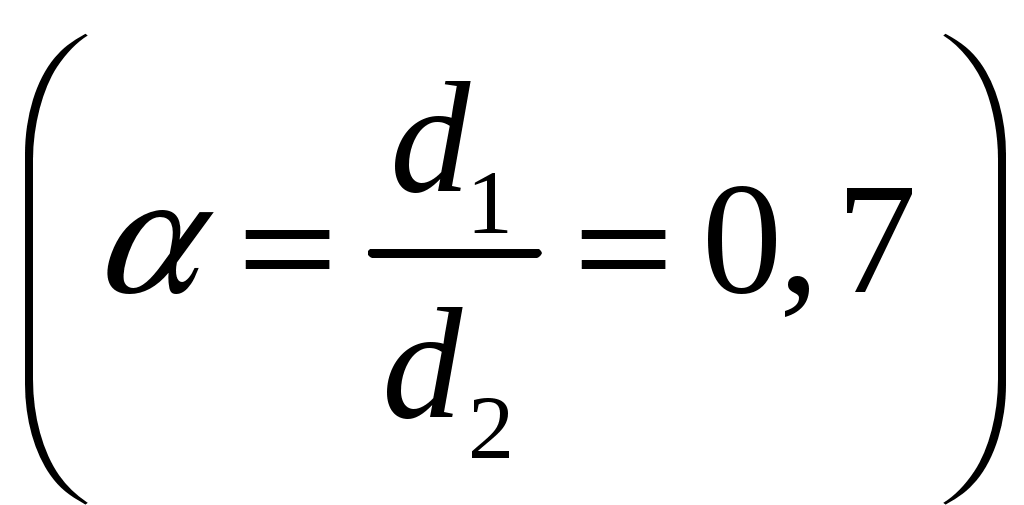 ;
;
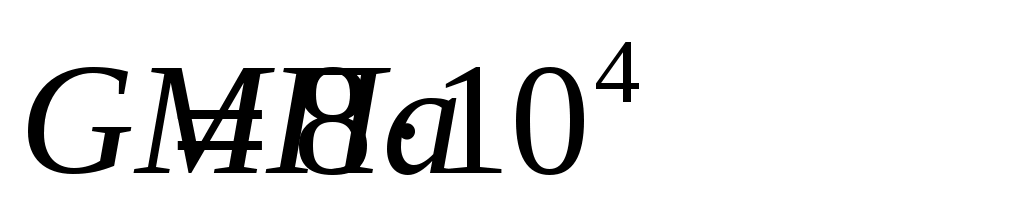 - модуль упругости второго рода.
- модуль упругости второго рода.
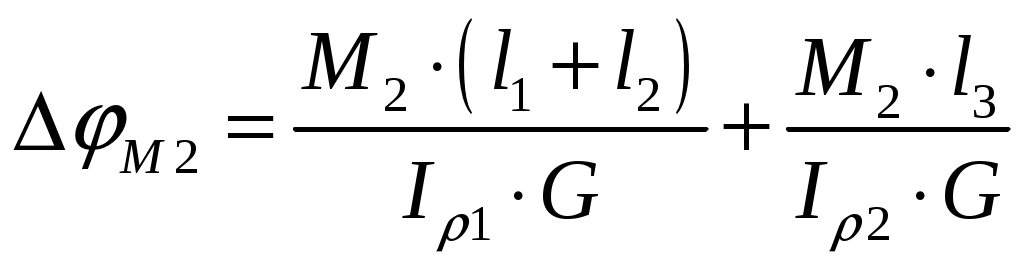 ,
,
где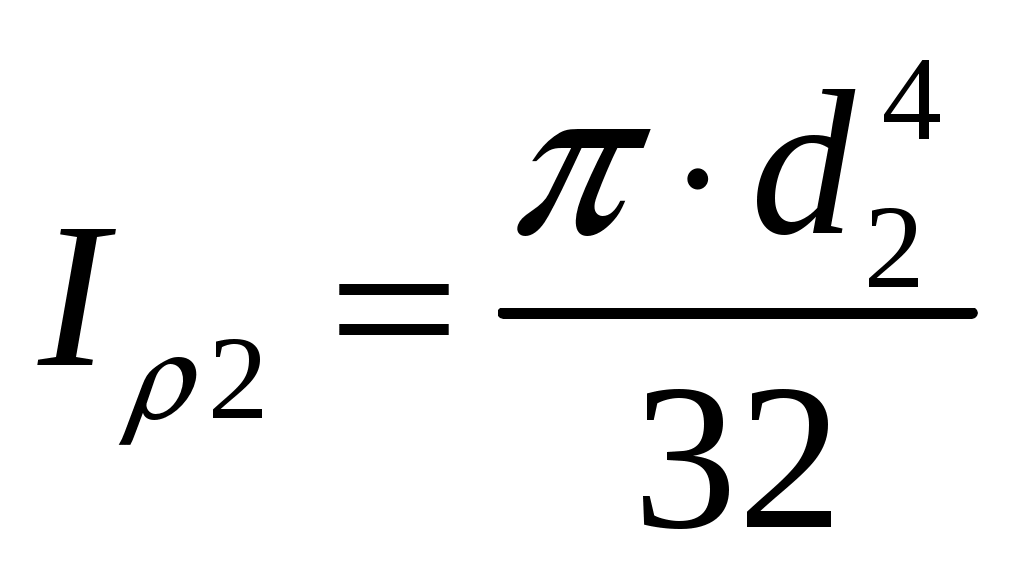 - полярный момент инерции сплошного сечения вала на участке
- полярный момент инерции сплошного сечения вала на участке 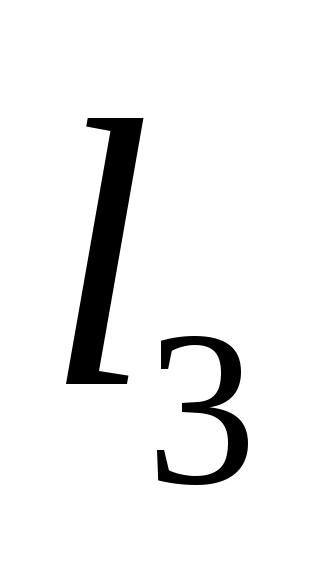 .
.
Тогда:
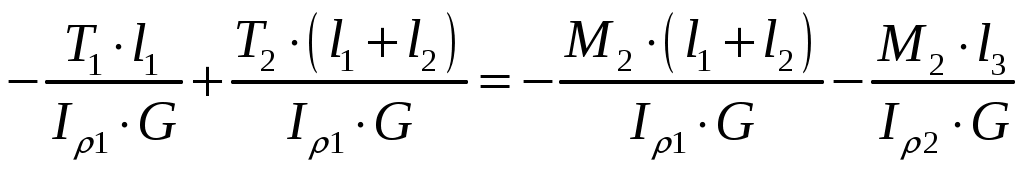 .
.
Учитывая, что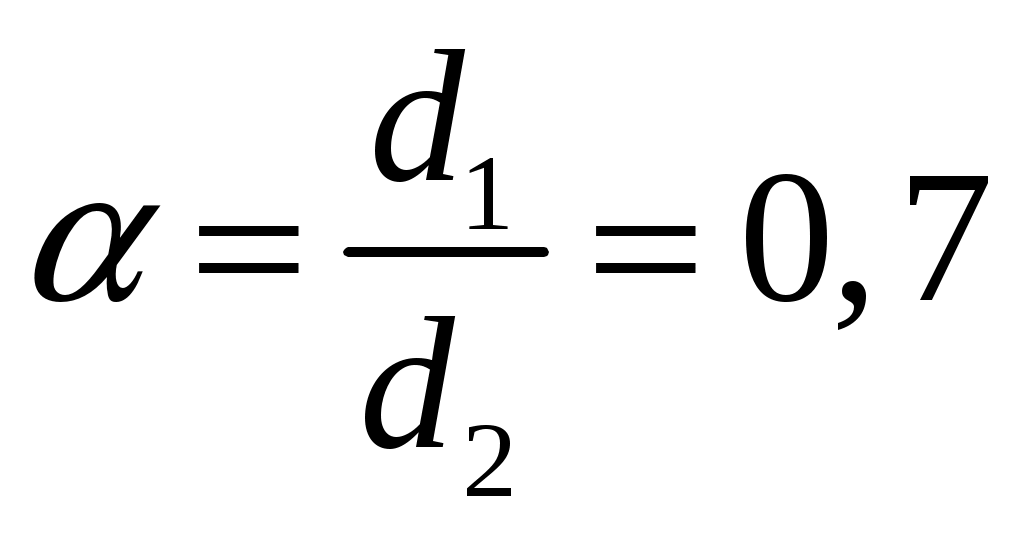 находим:
находим: 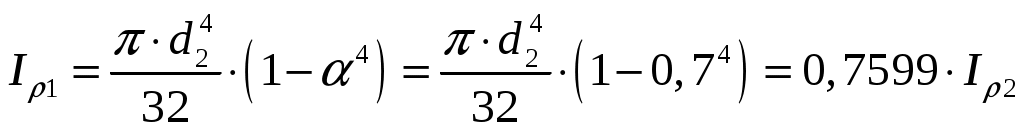 .
.
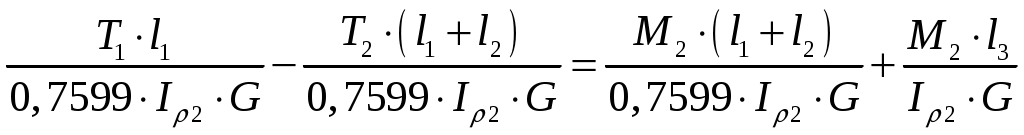 ;
;
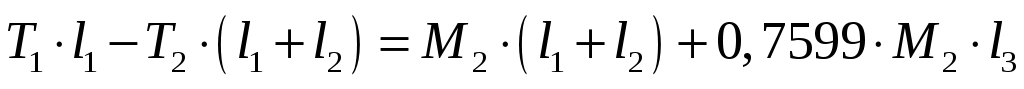 ;
;
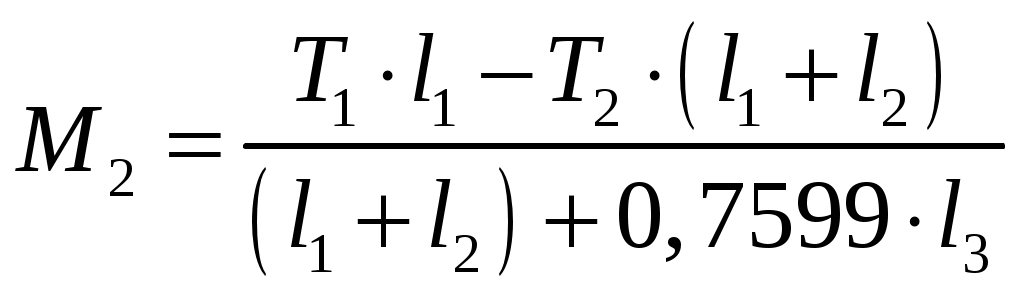
;
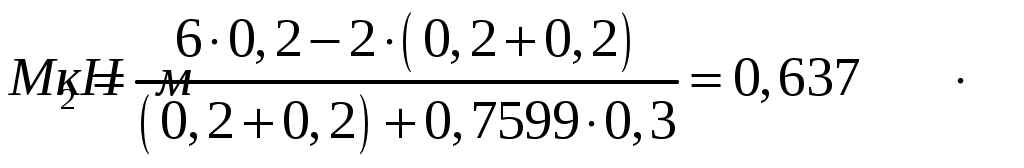 .
.
Зная величину крутящего момента, можем рассматривать брус как консольную балку и, не определяя реакции во второй заделке, найти опасное сечение, т.е. сечение, в котором возникают максимальные внутренние силовые факторы.
Строим эпюру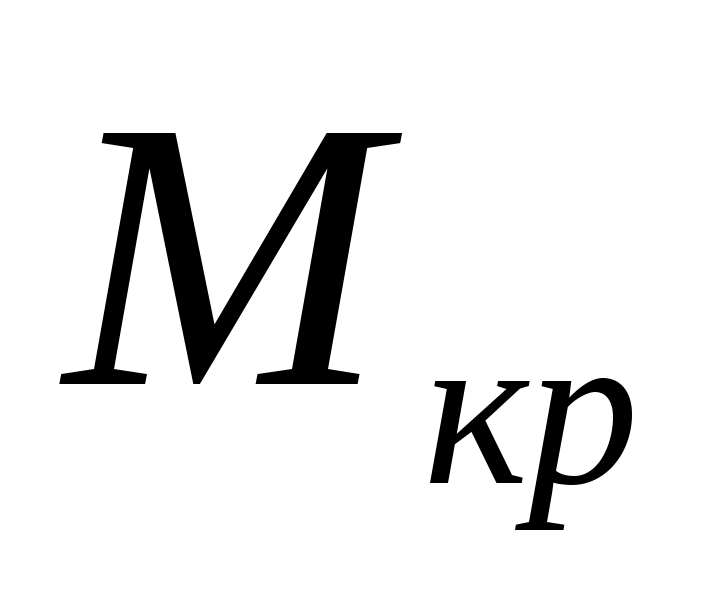 . Зная внешние моменты и используя метод сечений, определяем крутящие (внутренние) моменты. Идем справа налево:
. Зная внешние моменты и используя метод сечений, определяем крутящие (внутренние) моменты. Идем справа налево:
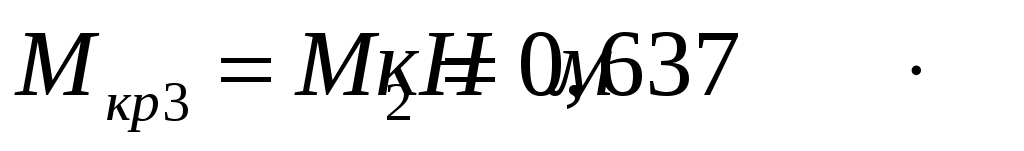 ;
;
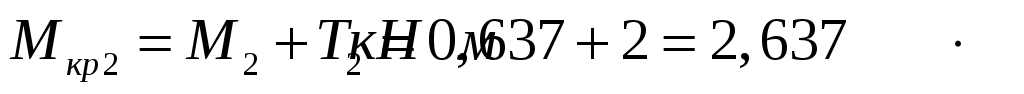 ;
;
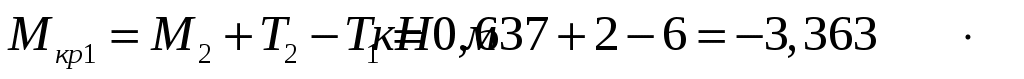
По полученным значениям строим эпюру крутящих моментов (рис. 7.4, б).
Из построенной эпюры крутящих моментов видно, максимальный момент действует на первом силовом участке, но возможно, что опасное сечение, с точки зрения прочности может оказаться на третьем силовом участке, так как полярный момент сопротивления сечения первого участка отличается от полярного момента сопротивления третьего участка. Найдем отношение касательного напряжения на первом участке к касательному напряжению на третьем участке
к касательному напряжению на третьем участке 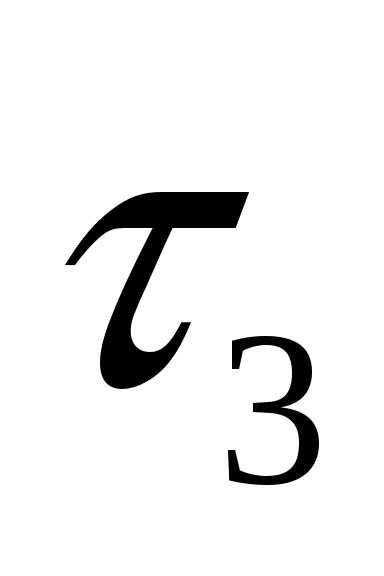 . Если это отношение окажется больше единицы, то опасным сечением будет являться сечение на первом участке и наоборот.
. Если это отношение окажется больше единицы, то опасным сечением будет являться сечение на первом участке и наоборот.
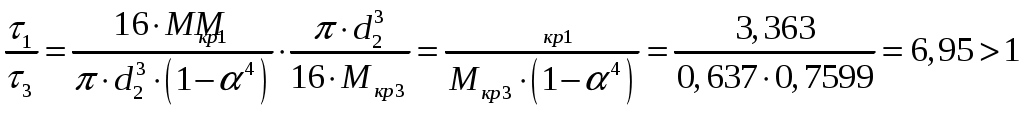 .
.
Для выявления опасного сечения, с точки зрения условия жесткости, находим отношение абсолютных углов закручивания на соответствующих участках:
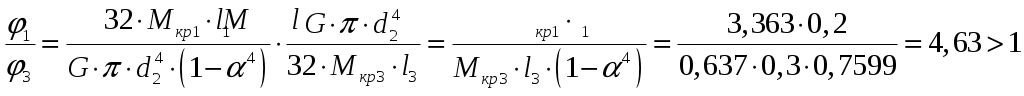 .
.
Следовательно, опасное сечение по условию прочности и жесткости находится на первом участке. Определяем диаметр первой ступеней из условия прочности:
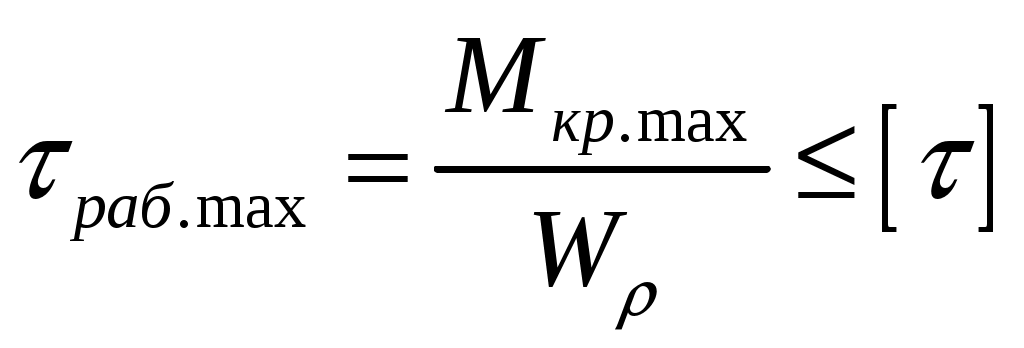 ,
,
где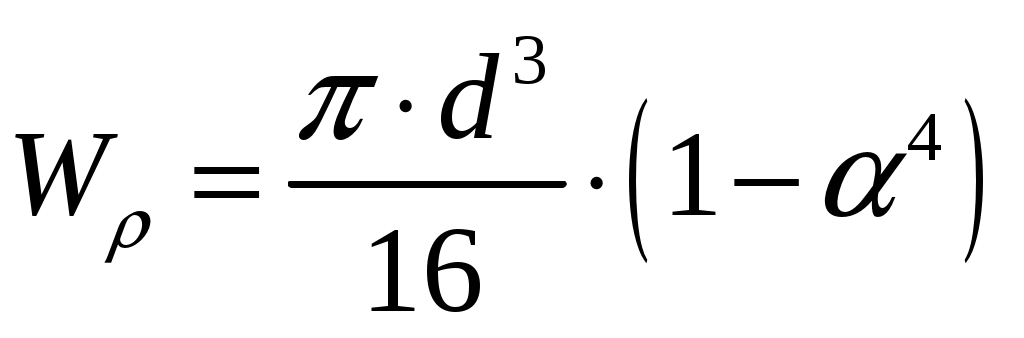 - полярный момент сопротивления кольцевого сечения.
- полярный момент сопротивления кольцевого сечения.
Тогда
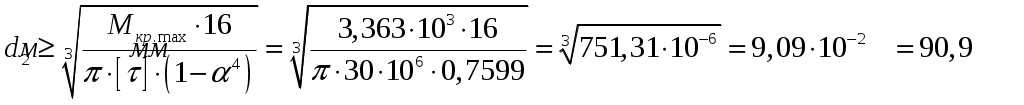
Для третьего участка:
По полученным значениям строим эпюру
Находим напряжения на каждом силовом участке.
По полученным значениям строим эпюру
Построение эпюры перемещений начинаем с левого конца бруса, который жестко защемлён, и, следовательно, перемещение его равно нулю. Построение эпюры перемещений ведем слева направо.
Для третьего силового участка на расстоянии
При
При
Для второго силового участка абсолютное удлинение равно:
При
При
Для первого силового участка абсолютное удлинение равно:
При
При

Рис. 4.5. Эпюры
То есть перемещение левого конца бруса равно величине зазора. По полученным значениям строим эпюру
3. Анализируя полученные результаты, видим, наличие правой заделки при существующем зазоре в 1,0 мм дало возможность понизить рабочее напряжение на третьем участке, и перераспределить его на другие участки. Таким образом, меняя величину зазора, можно регулировать и значение внутренних усилий, возникающих в сечениях бруса под действием приложенных нагрузок.
Правильность решения задачи можно проверить по эпюре деформаций. Равенство перемещения правого сечения бруса величине зазора говорит об этом.
Задача № 7
На стальной ступенчатый брус круглого поперечного сечения, закрепленного с двух сторон, действуют скручивающие моменты сил.
1. Определить диаметры стержня из условия прочности и условия жесткости.
2. Построить эпюры крутящих моментов и абсолютных углов закручивания при принятых диаметрах ступеней стержня.
3. Определить рабочие максимальные касательные напряжения и сравнить с допускаемыми касательными напряжениями.
4. Определить действительный относительный угол закручивания и сравнить с допускаемым относительным углом закручивания.
Исходные данные:
;
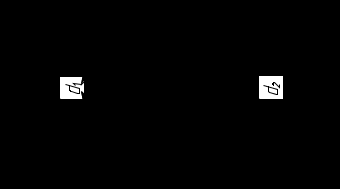
Рис. 7.1. Исходная схема.
Решение:
1. Освобождаем стержень от связей, которыми являются заделки с двух сторон, и заменяем действие связей силами реакций. Учитывая, что стержень невесомый и на него действуют только скручивающие моменты
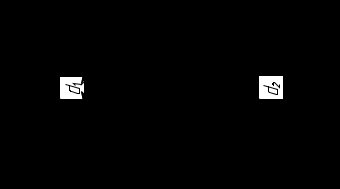
Рис. 7.2. Расчетная схема.
Для определения неизвестных моментов связей составляем уравнение статики. Для такой системы сил статика позволяет записать только одно уравнение равновесия:
Проводя анализ, видим, что при одном уравнение статики имеем два неизвестных
Для раскрытия статической неопределимости воспользуемся методом деформации применительно к кручению. Освободим, например, только правую заделку стального ступенчатого бруса и заменим её действие моментом связи
радиус

Рис. 7.3.
Это и будет являться уравнением деформации при кручении и вторым уравнением, необходимым для раскрытия статической неопределимости.
Найдем абсолютные углы закручивания:
где
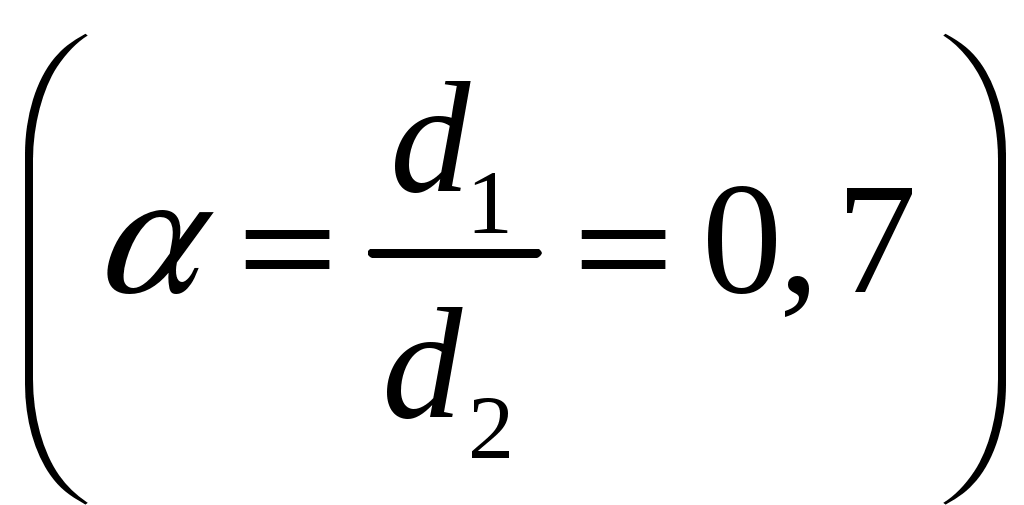 ;
;где
Тогда:
Учитывая, что
;
Зная величину крутящего момента, можем рассматривать брус как консольную балку и, не определяя реакции во второй заделке, найти опасное сечение, т.е. сечение, в котором возникают максимальные внутренние силовые факторы.
Строим эпюру
По полученным значениям строим эпюру крутящих моментов (рис. 7.4, б).
Из построенной эпюры крутящих моментов видно, максимальный момент действует на первом силовом участке, но возможно, что опасное сечение, с точки зрения прочности может оказаться на третьем силовом участке, так как полярный момент сопротивления сечения первого участка отличается от полярного момента сопротивления третьего участка. Найдем отношение касательного напряжения на первом участке
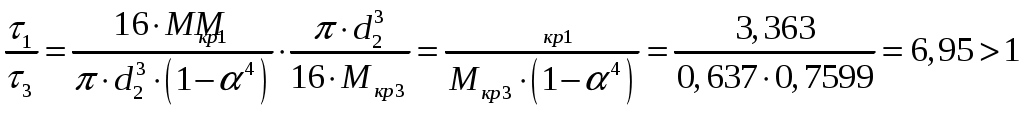 .
.Для выявления опасного сечения, с точки зрения условия жесткости, находим отношение абсолютных углов закручивания на соответствующих участках:
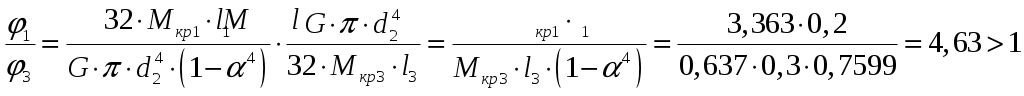 .
.Следовательно, опасное сечение по условию прочности и жесткости находится на первом участке. Определяем диаметр первой ступеней из условия прочности:
где
Тогда