Файл: Расчетнографическая работа по дисциплине Прикладная механика Работу.doc
Добавлен: 07.11.2023
Просмотров: 30
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Определяем диаметр первой ступени из условия жесткости:
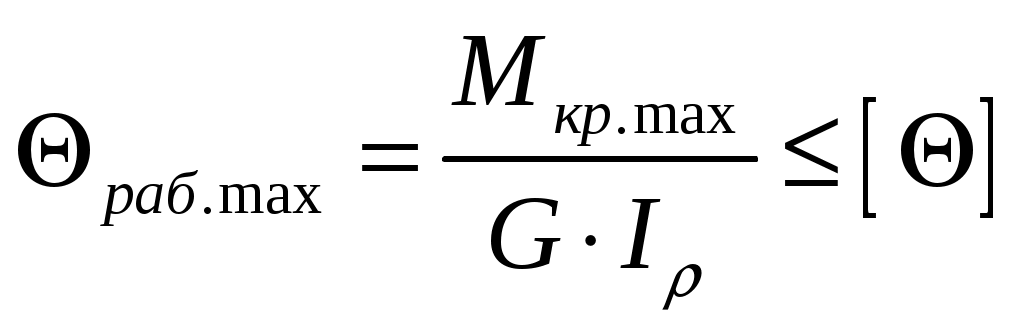 ,
,
где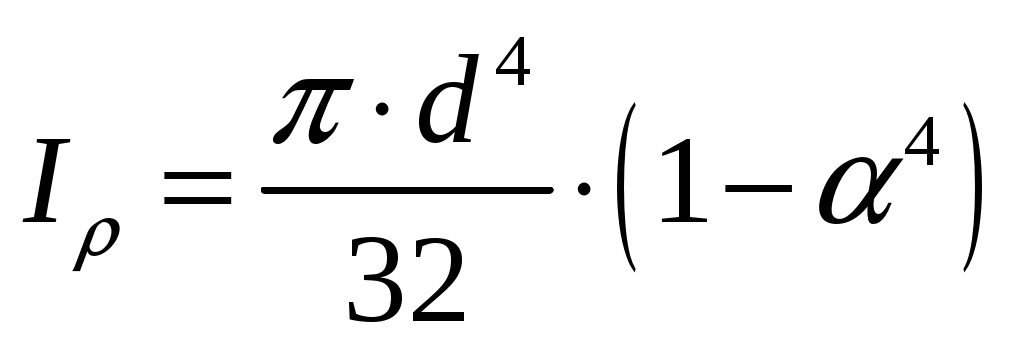 - полярный момент инерции кольцевого сечения;
- полярный момент инерции кольцевого сечения;
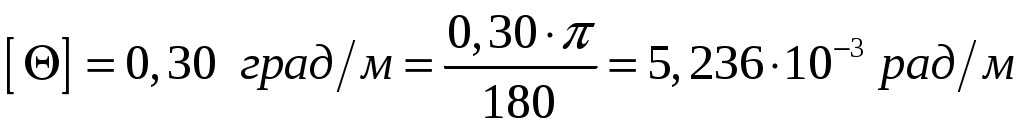 .
.
Тогда
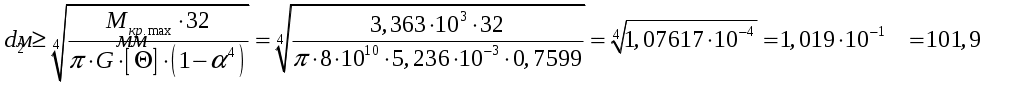 .
.
Принимаем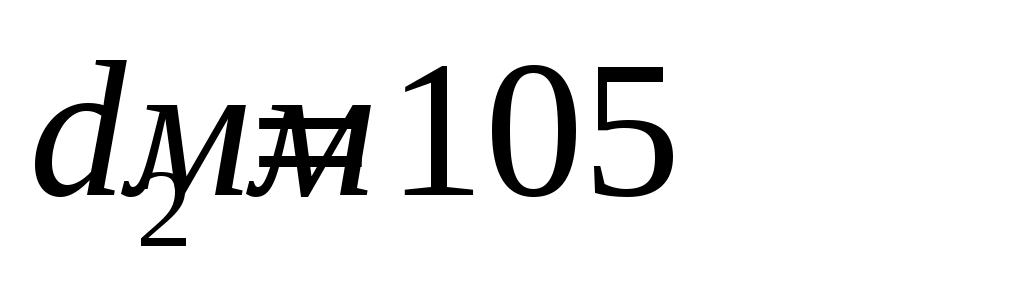 , тогда
, тогда 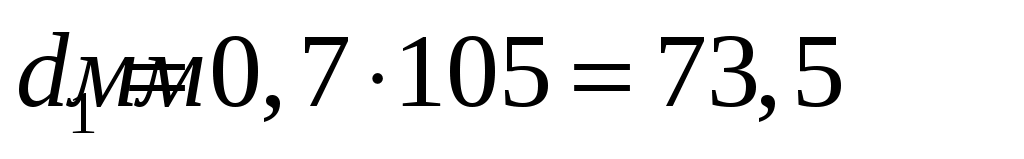 .
.
2. Определив размеры сечений бруса, строим эпюры максимальных касательных напряжений и абсолютных углов закручивания (рис. 7.4, в, г).
На первом участке:
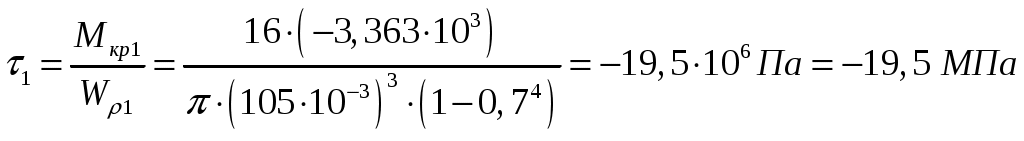 ;
;
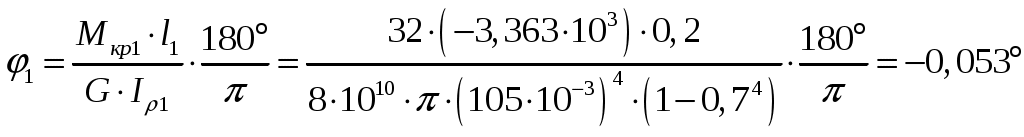 .
.
На втором участке:
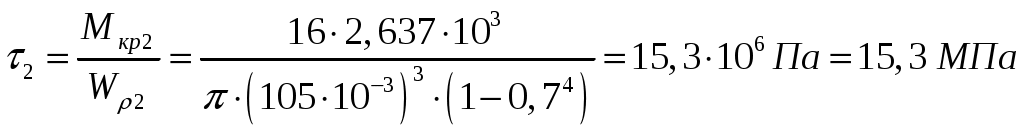 ;
;
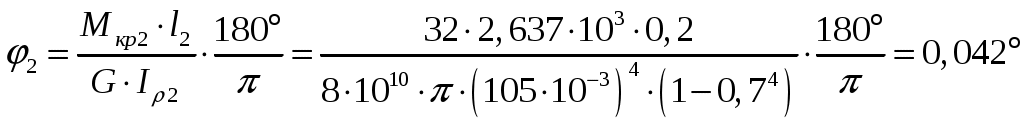 .
.
На третьем участке:
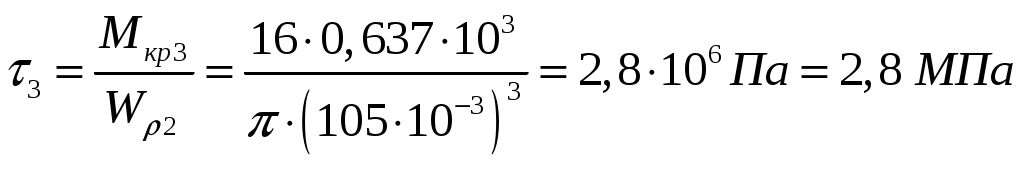 ;
;
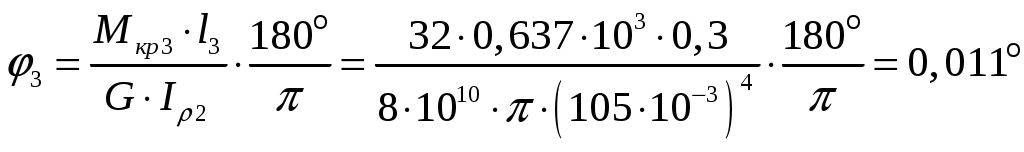 .
.
Проверяем угол закручивания на правом конце балки:
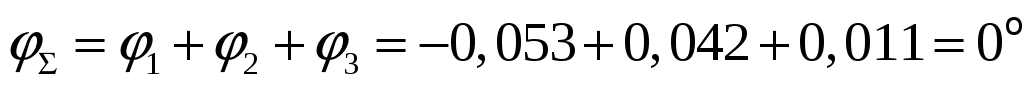 .
.
Угол закручивания правого конца балки равен нулю, следовательно, задача решена правильно.
3. Сравниваем максимальное касательное напряжение с допускаемым касательным напряжением:
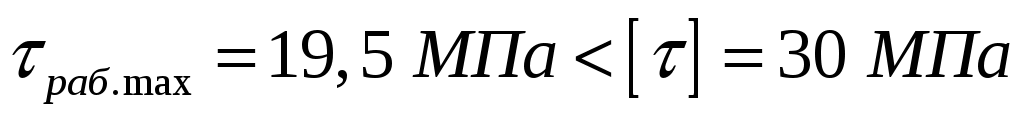 .
.
4. Определяем рабочий максимальный относительный угол закручивания и сравниваем его с допускаемым.
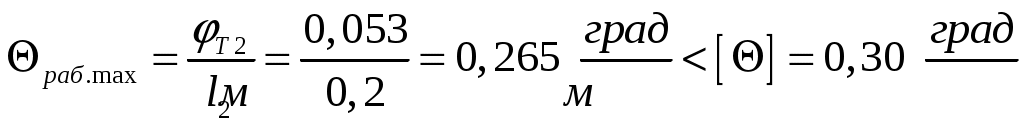 .
.
На всех участках стержня выполняются как условия прочности, так и условие жесткости. Значительно меньшее рабочее касательное напряжение получилось вследствие того, что окончательные размеры сечений были приняты из расчета на жесткость.
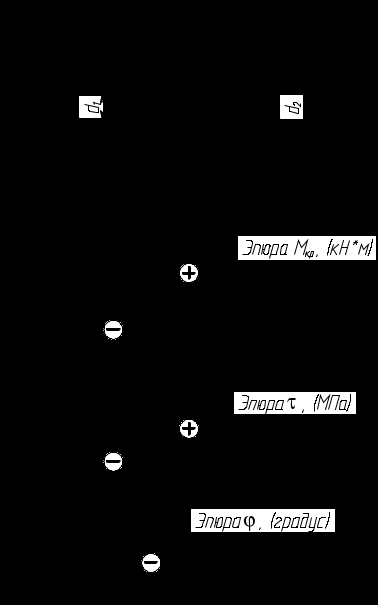
Рис. 7.4. Эпюры.
Задача № 8
Для заданной балки (рис.8.1) по исходным данным требуется:
1) построить расчетную схему балки в выбранном масштабе;
2) построить эпюры поперечных сил и изгибающих моментов;
3) из условия прочности при изгибе определить номер профиля двутавровой балки в соответствии с ГОСТ 8239-89, приняв допускаемое нормальное напряжение равным .
.
4) построить эпюру перемещений сечений балки.
Исходные данные: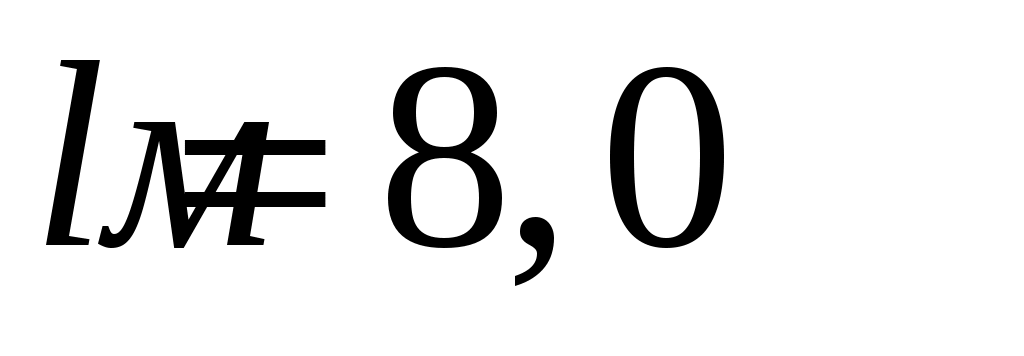 ,
, 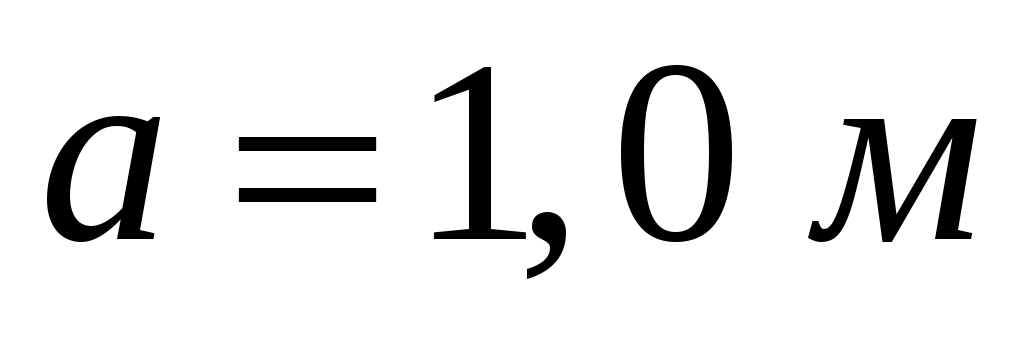 ,
, 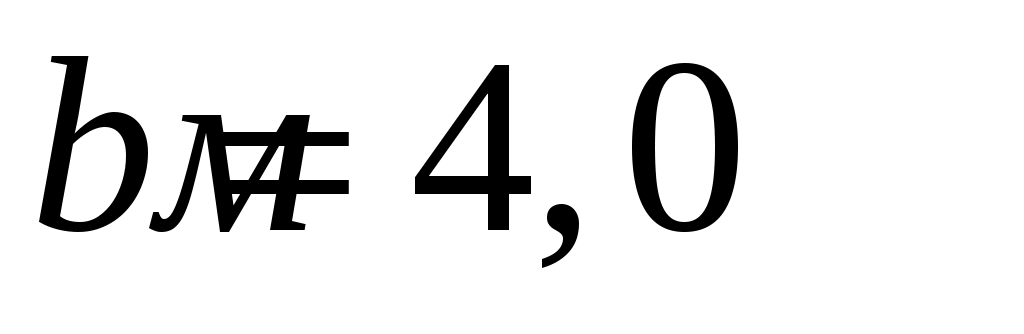 ,
, 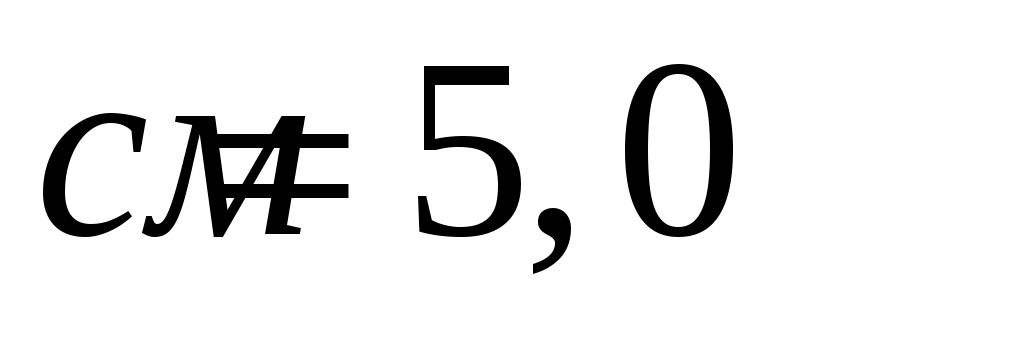 ,
, 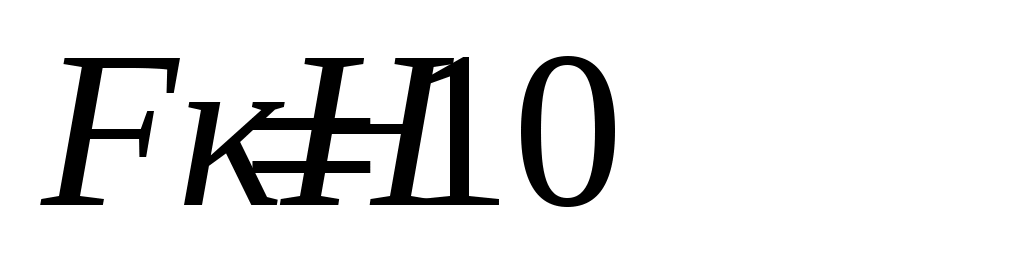 ,
, 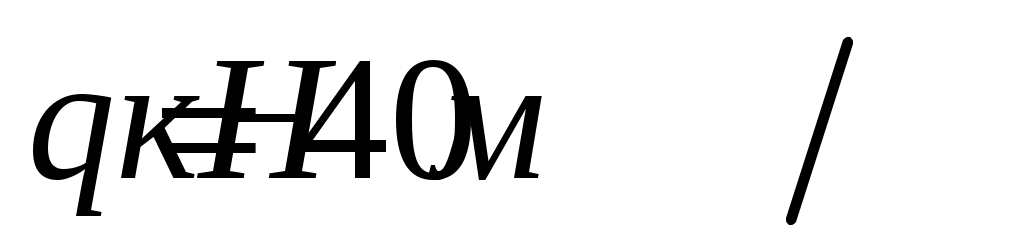 ,
, 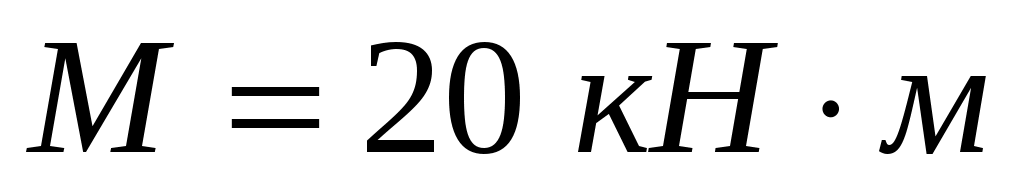 .
.

Рис. 8.1. Двухопорная балка.
Решение:
1. Освобождаем балку от связей и заменяем действие связей силами реакций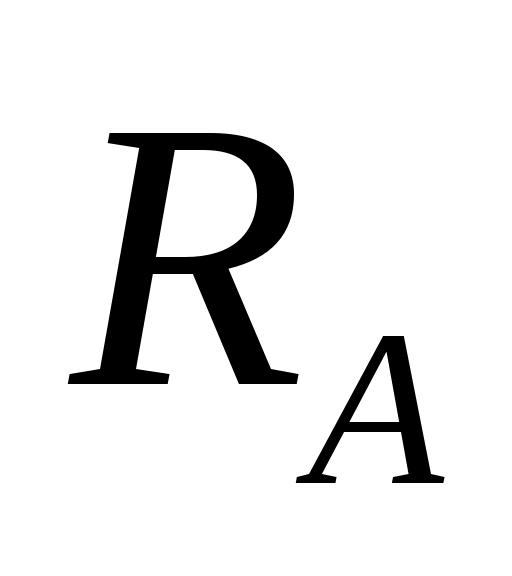 и
и 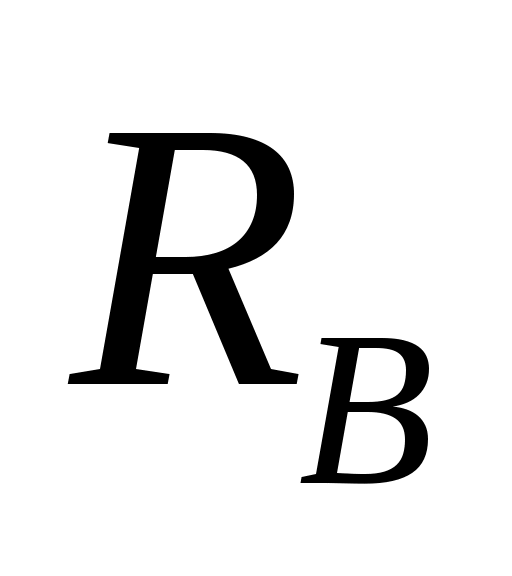 . На балку действует плоская параллельная система сил, для которой необходимо и достаточно составить два уравнения статики. Составим уравнения равновесия:
. На балку действует плоская параллельная система сил, для которой необходимо и достаточно составить два уравнения статики. Составим уравнения равновесия:
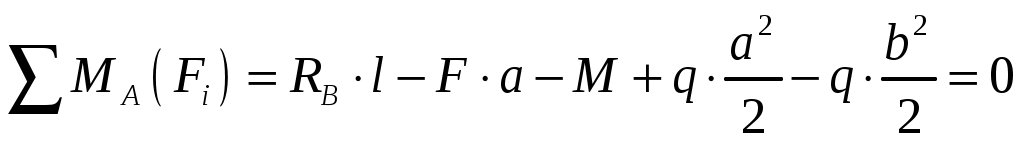 ; (1)
; (1)
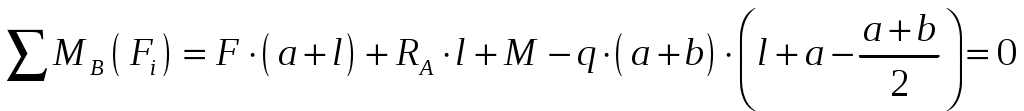 ; (2)
; (2)
Из уравнения (1) находим:
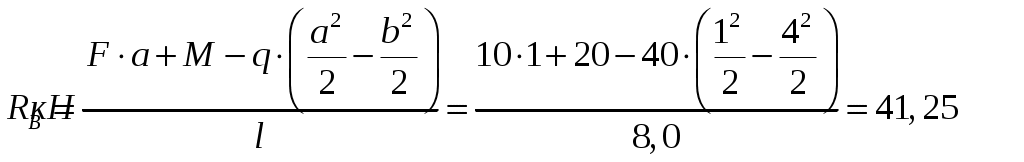 .
.
Из уравнения (2) находим:
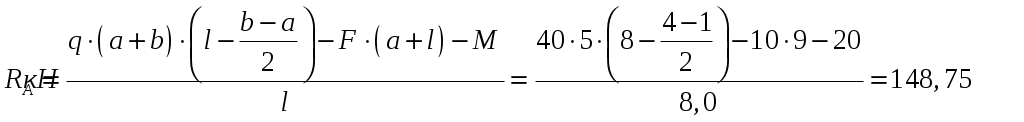 .
.
Проверка: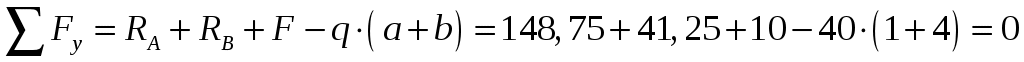 .
.
Следовательно, реакции связей определены верно.
2. Разбиваем балку на силовые участки.
Анализ внутренних силовых факторов:
На первом участке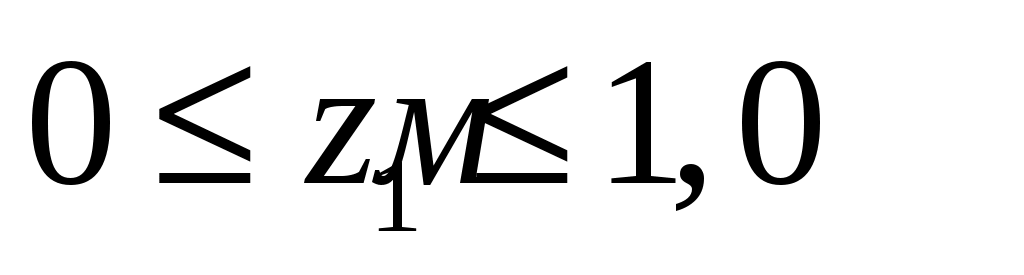 :
:
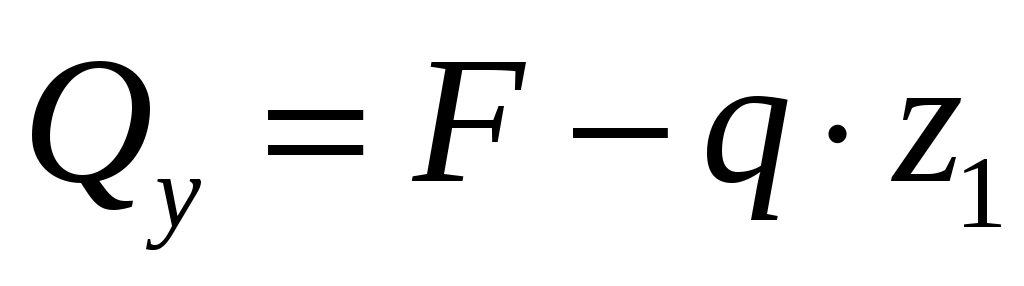
;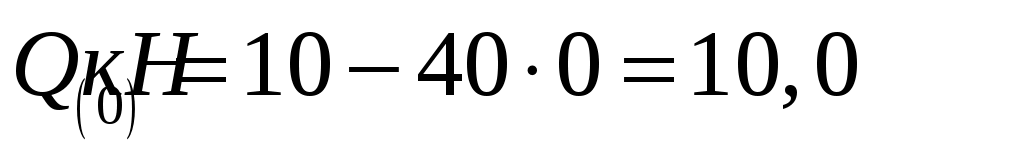 ,
, 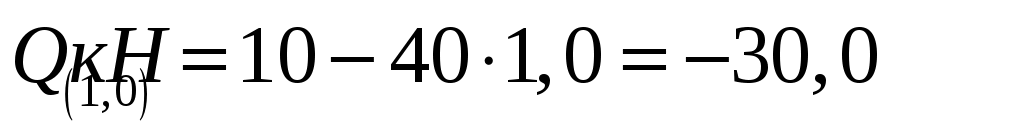 .
.
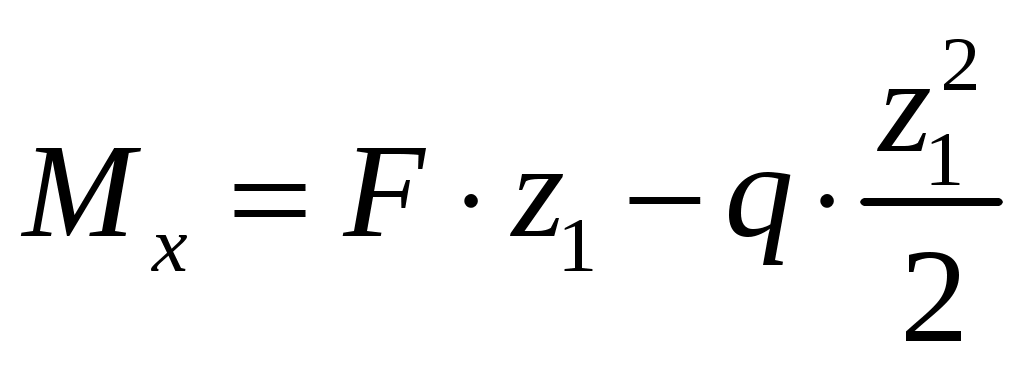 ;
; 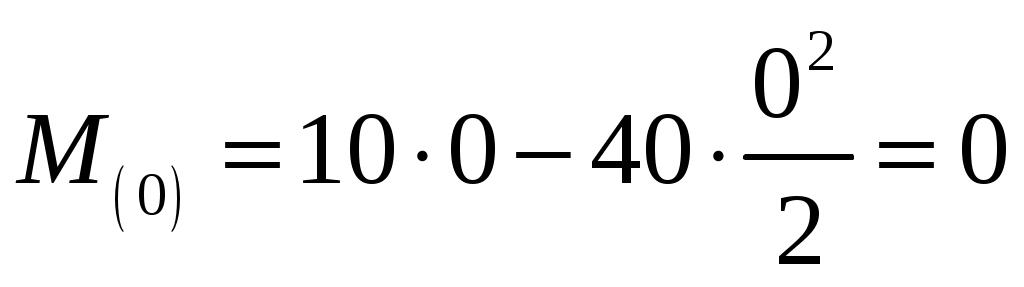 ,
, 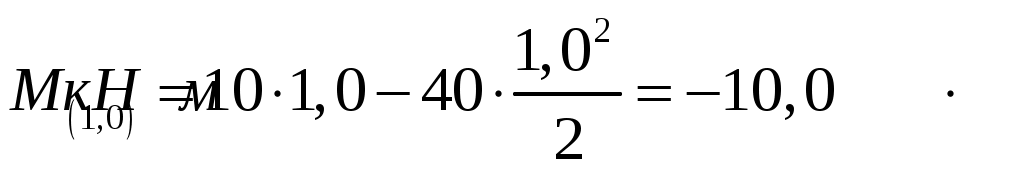 .
.
Эпюра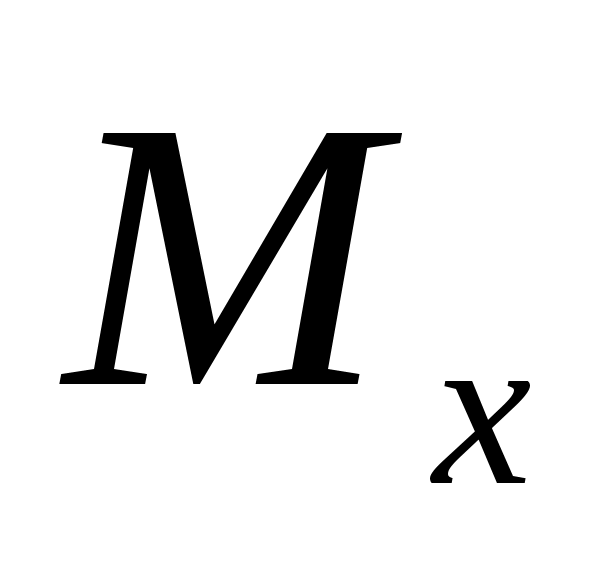 на первом участке представляет собой параболу, находим значение эпюры в точке максимума, где
на первом участке представляет собой параболу, находим значение эпюры в точке максимума, где 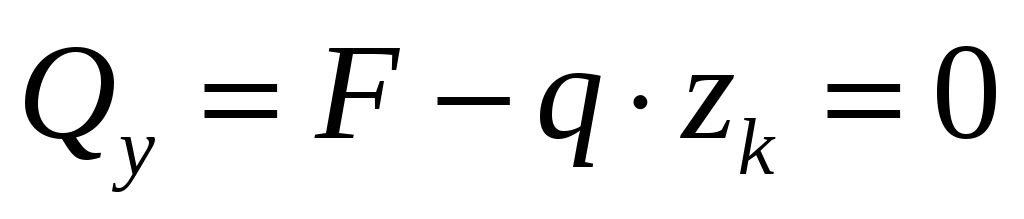 , т.е.
, т.е. 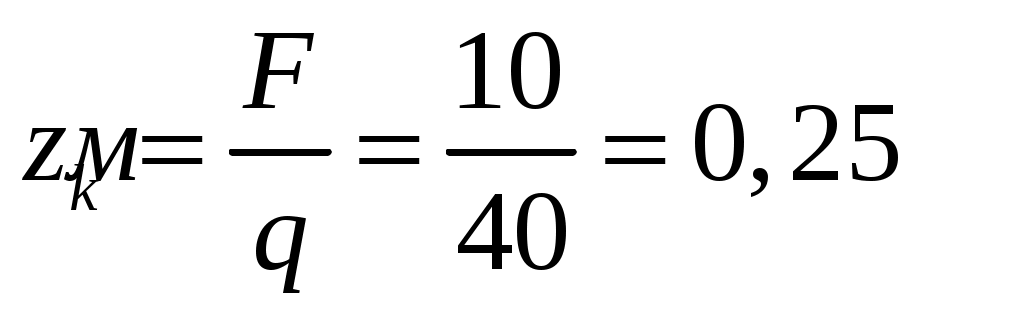 :
:
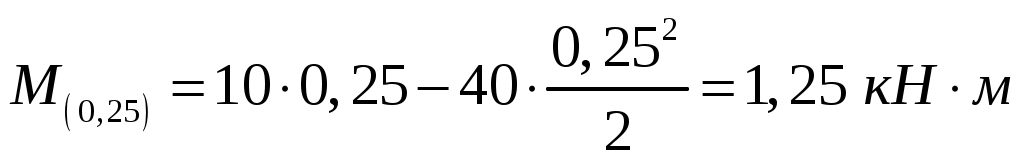 .
.
На втором участке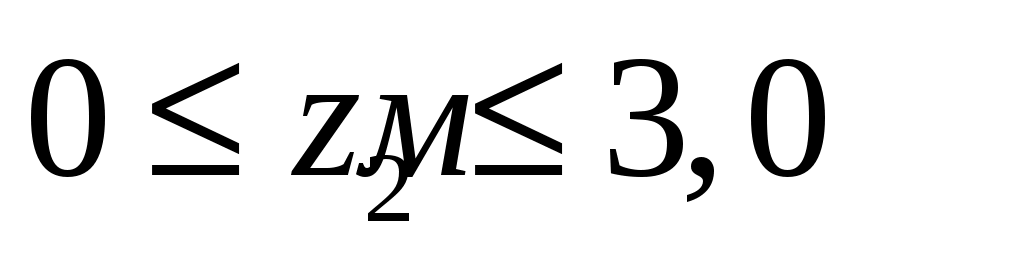 ;
;
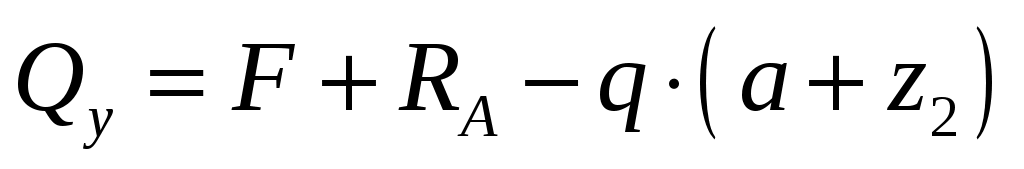 ;
; 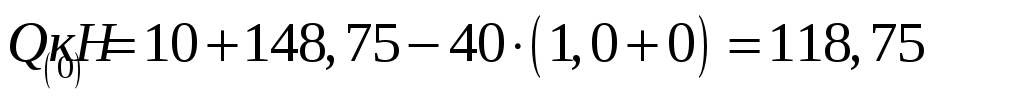 ,
,
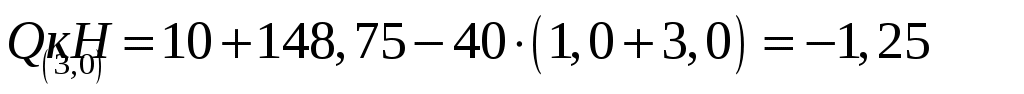 .
.
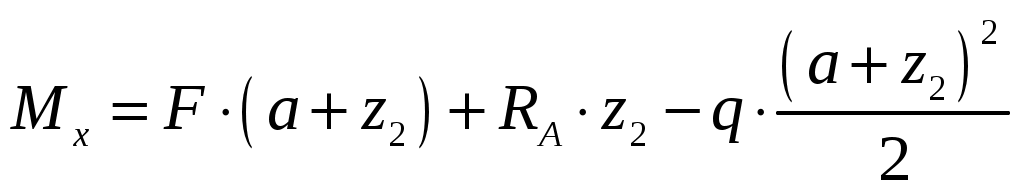 ;
; 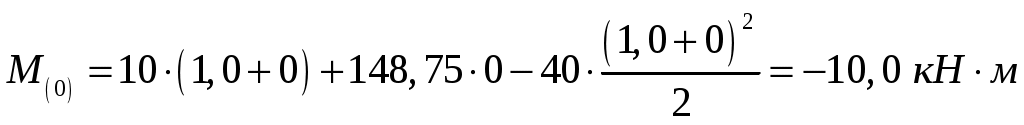 ,
,
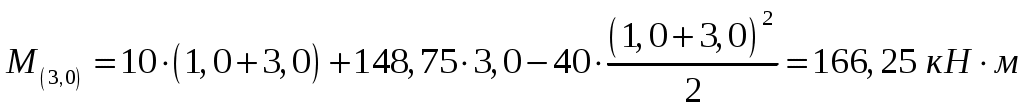 .
.
Эпюра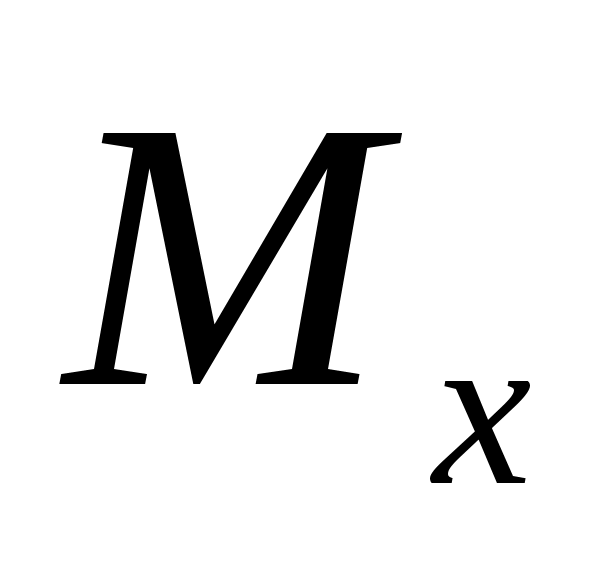 на втором участке представляет собой параболу, находим значение эпюры в точке максимума, где
на втором участке представляет собой параболу, находим значение эпюры в точке максимума, где 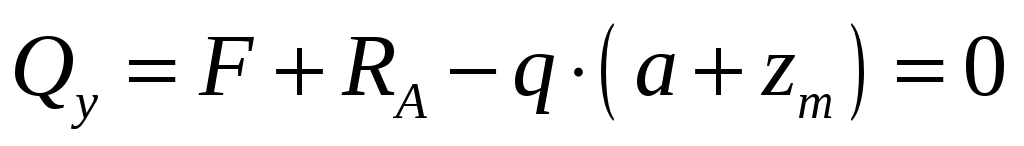 , т.е.
, т.е.
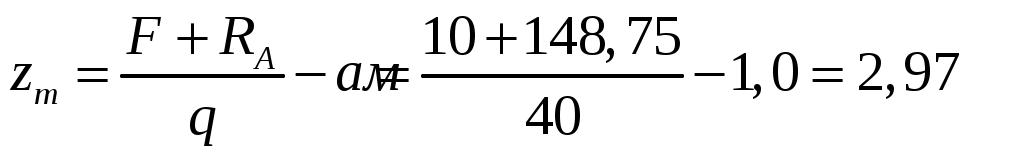 :
:
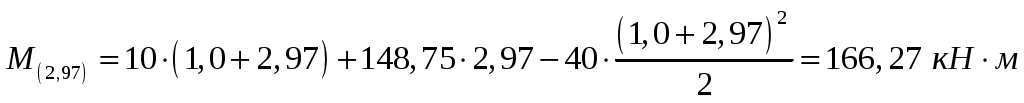
На третьем участке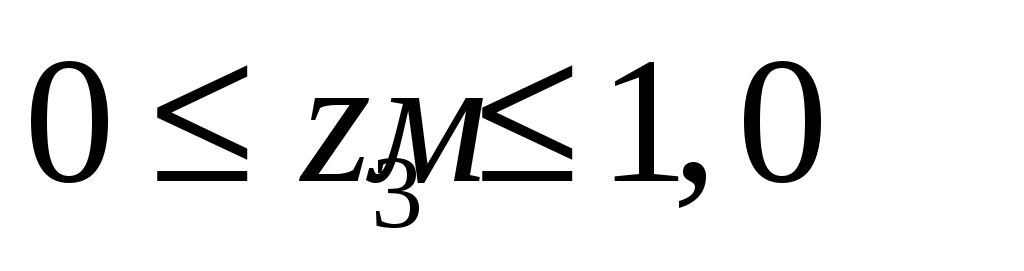 ;
;
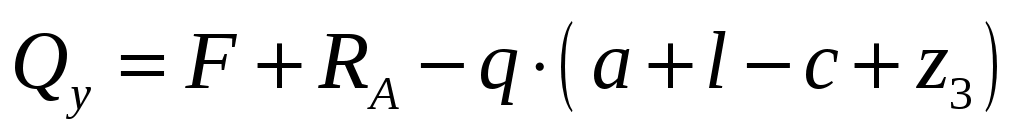 ;
; 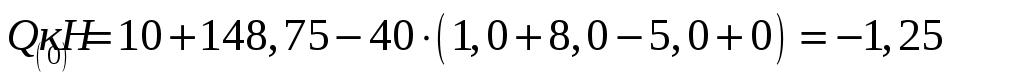 ,
,
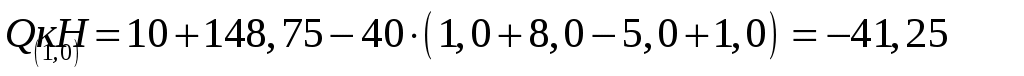 .
.
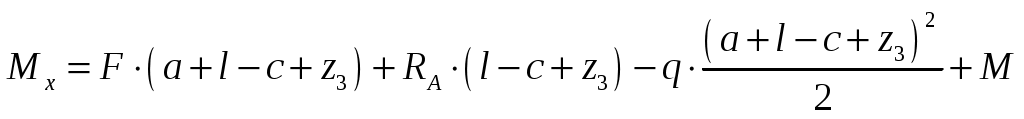
;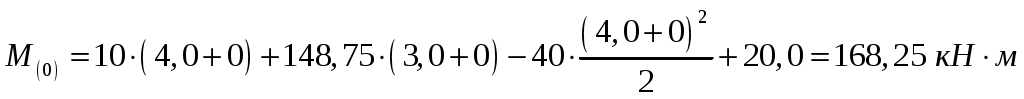 ,
,
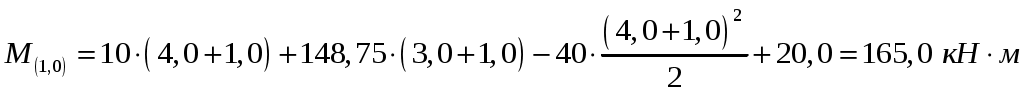 .
.
Эпюра на втором участке представляет собой параболу, находим значение эпюры в середине участка:
на втором участке представляет собой параболу, находим значение эпюры в середине участка:
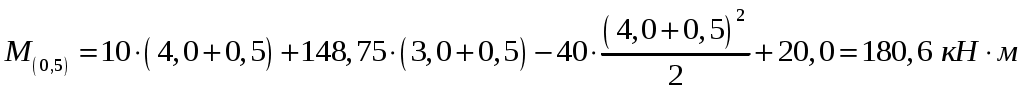
На четвертом участке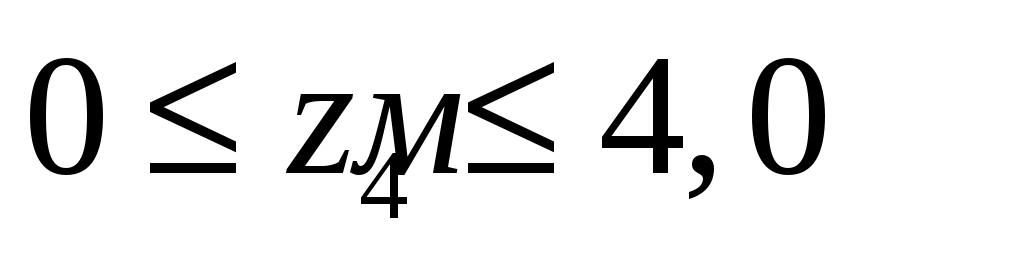 :
:
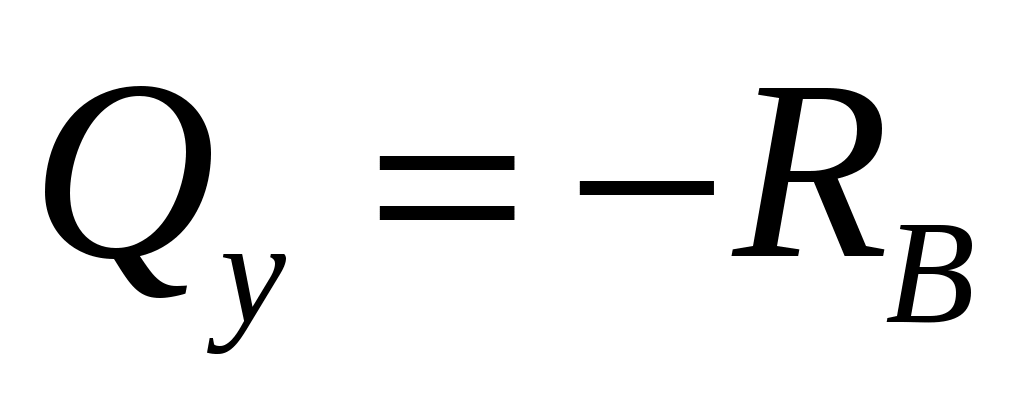 ;
; 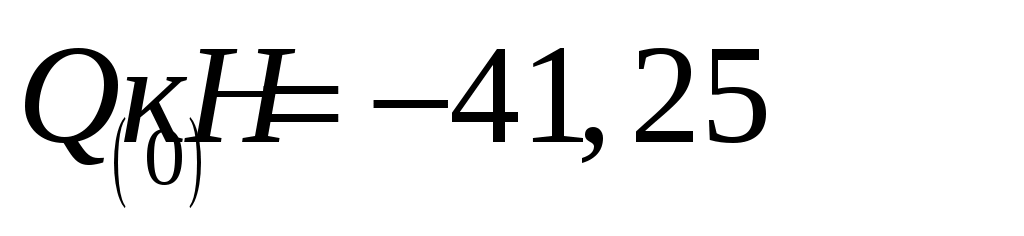 ,
, 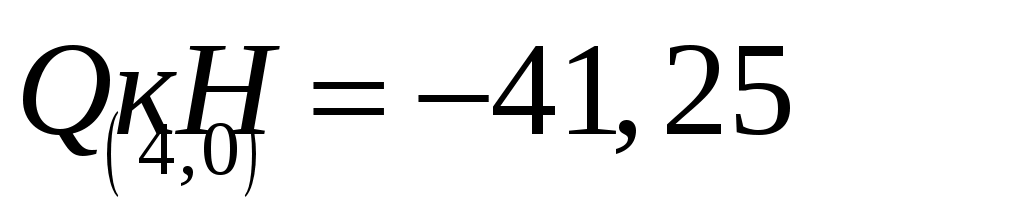 .
.
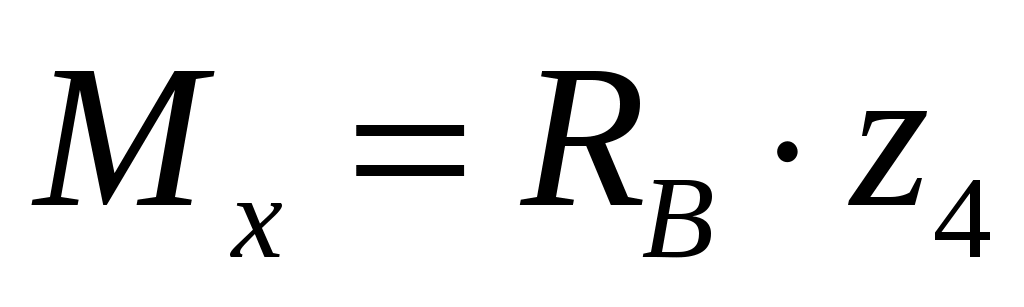 ;
; 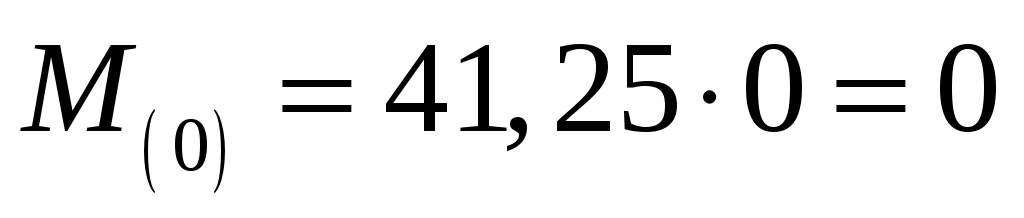 ,
, 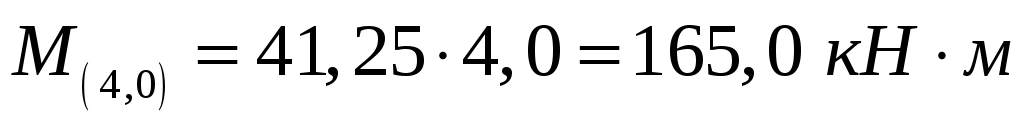 .
.
Эпюры поперечных сил и изгибающих моментов приведены на рис. 8.2, б, в. Из построенных эпюр видно, что максимальный изгибающий момент равен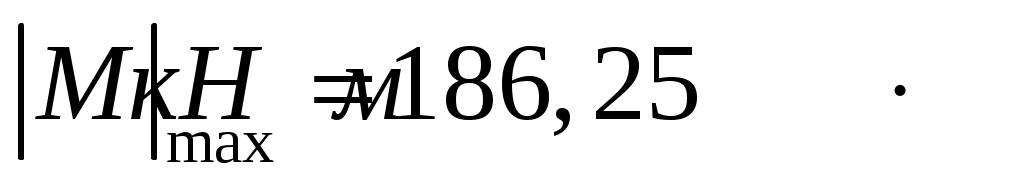 и действует в сечении приложения внешнего момента.
и действует в сечении приложения внешнего момента.
3. Из условия прочности по нормальным напряжениям подбираем сечение:
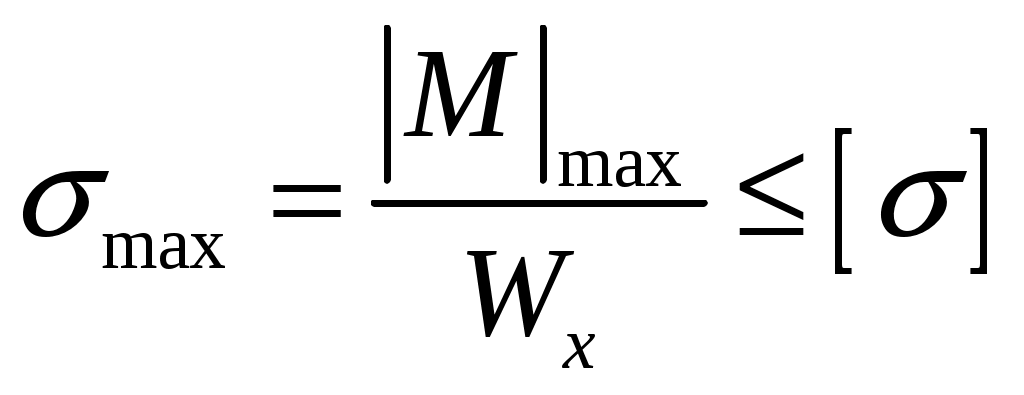
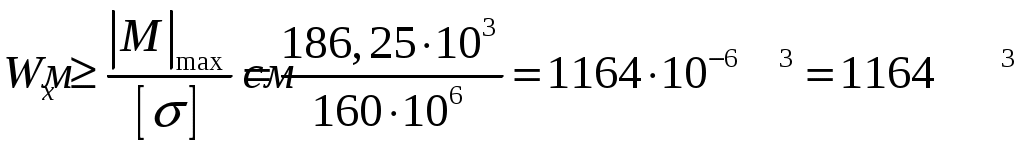 .
.
По ГОСТ 8239-89 ближайший номер двутавра № 45 с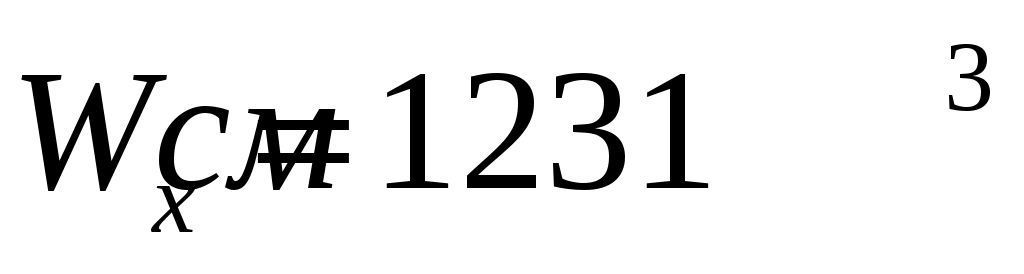 ,
, 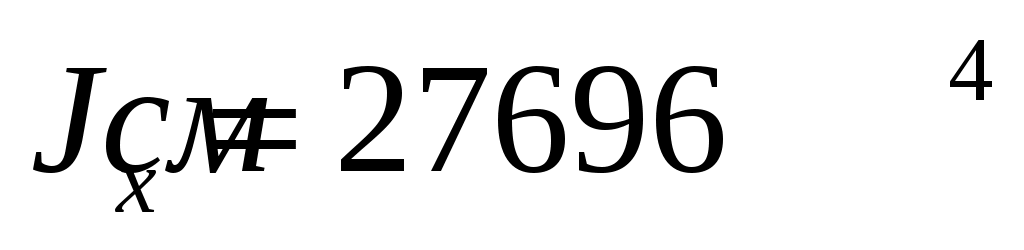 .
.
4. Для балки с принятыми размерами определим перемещения сечений по универсальному уравнению изогнутой оси линии. Выберем начало координат в левом крайнем сечении (точка приложения силы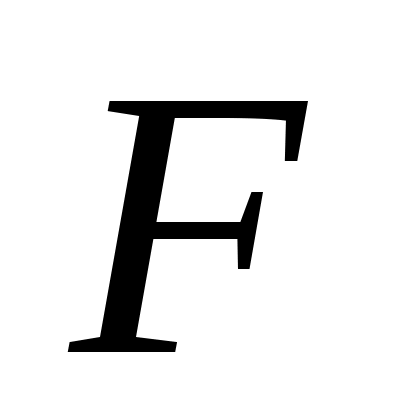 ) и запишем универсальные уравнения для последнего участка:
) и запишем универсальные уравнения для последнего участка:
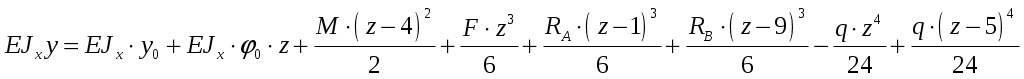 (3)
(3)

Рис. 8.2. Эпюры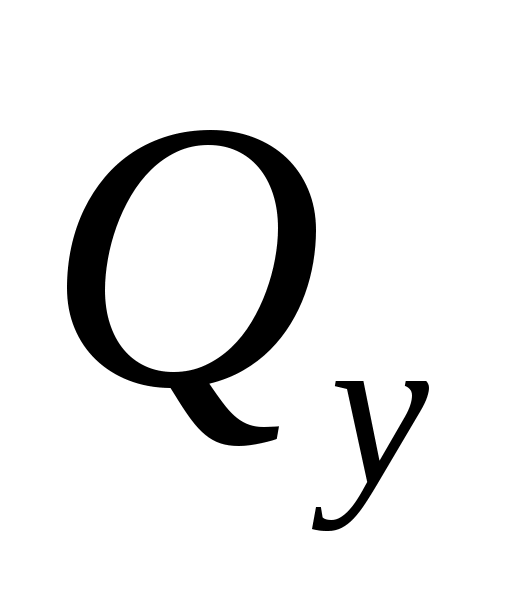
,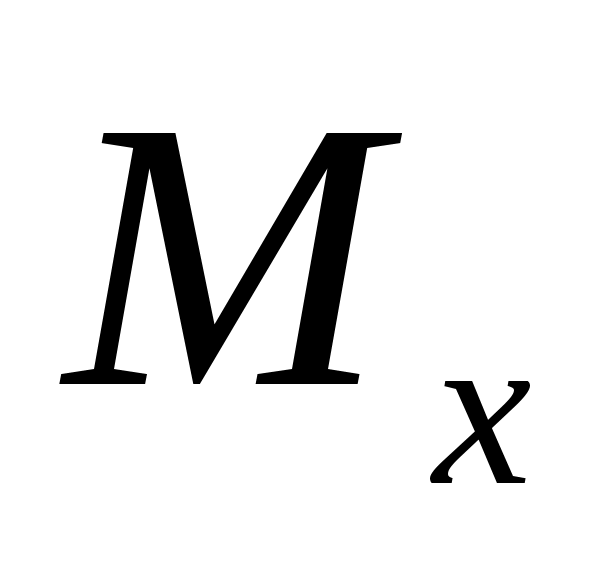 ,
, 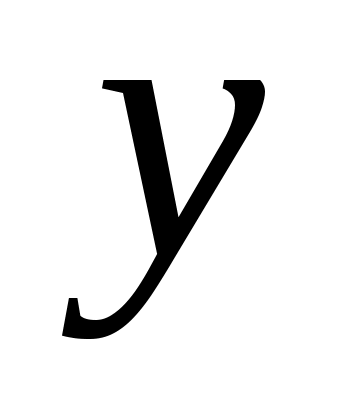 .
.
В этом уравнении два неизвестных постоянных интегрирования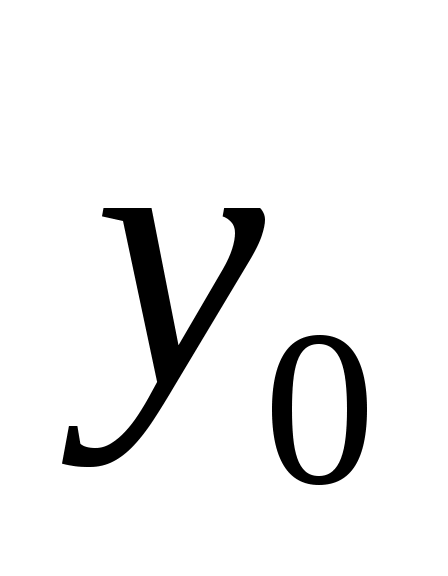 и
и  . Значения этих неизвестных найдем из начальных параметров: при
. Значения этих неизвестных найдем из начальных параметров: при 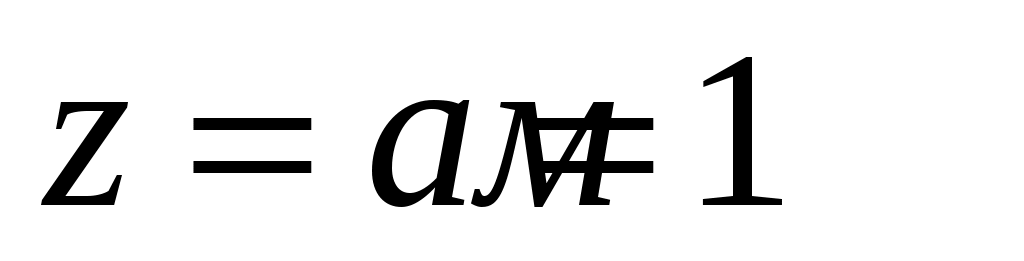
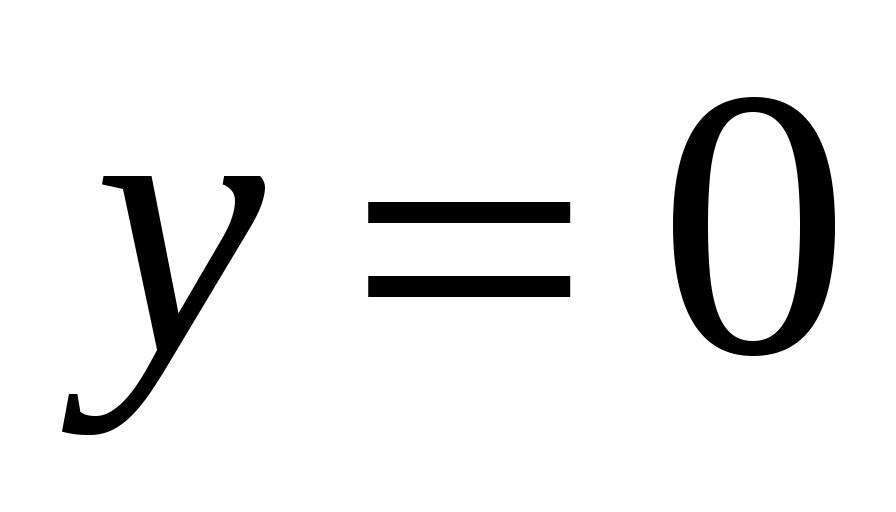 , и при
, и при 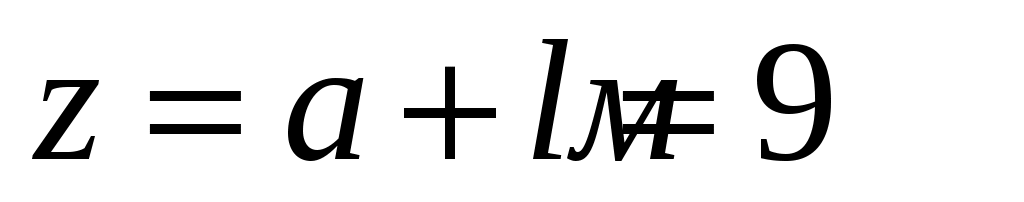
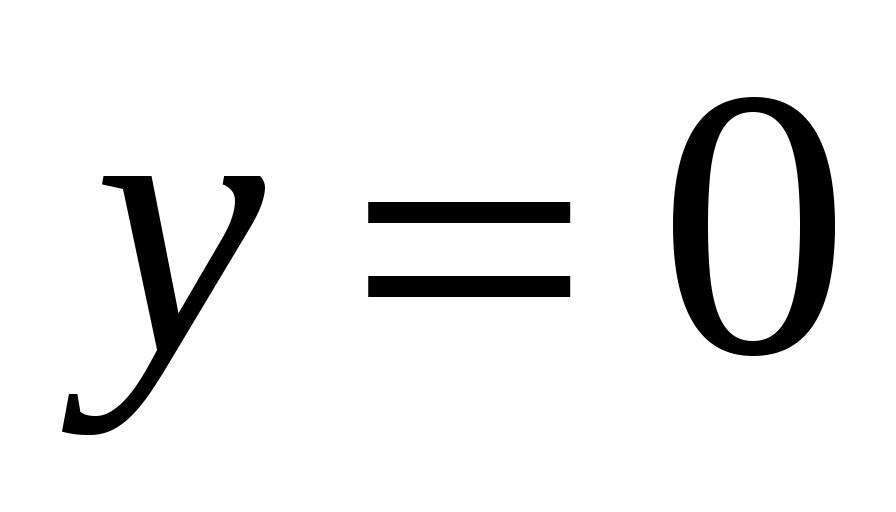 . Тогда:
. Тогда:
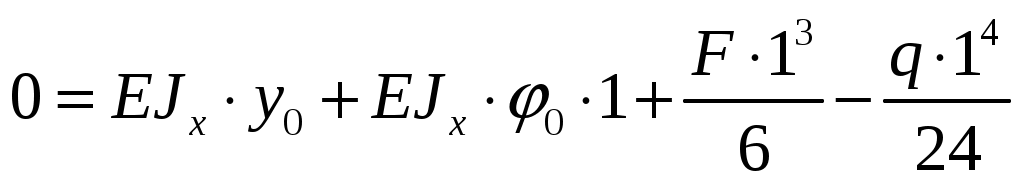 ; 4)
; 4)
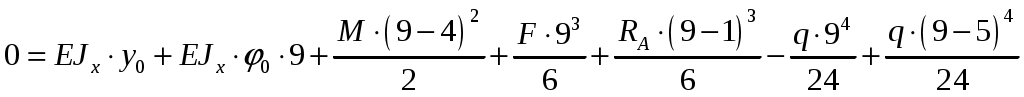 . (5)
. (5)
Решая совместно уравнения (4) и (5), находим значения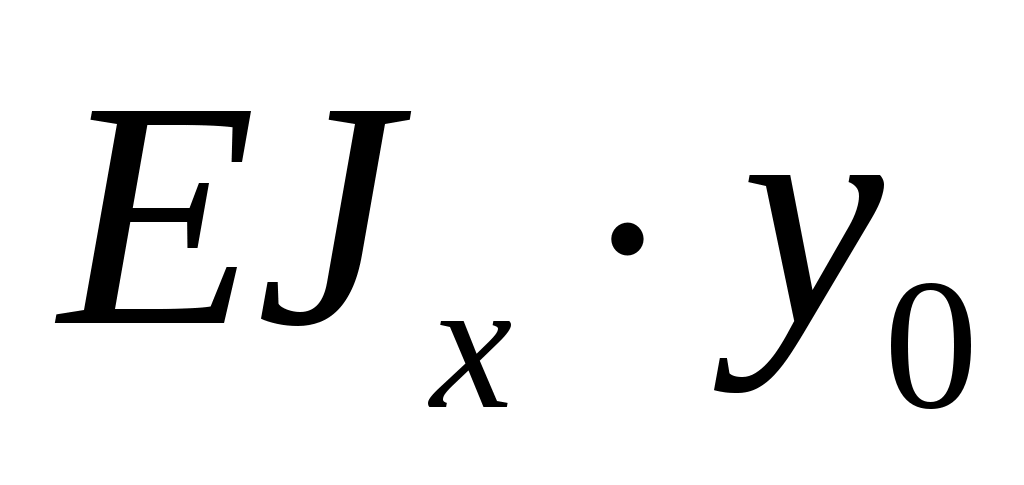 и
и 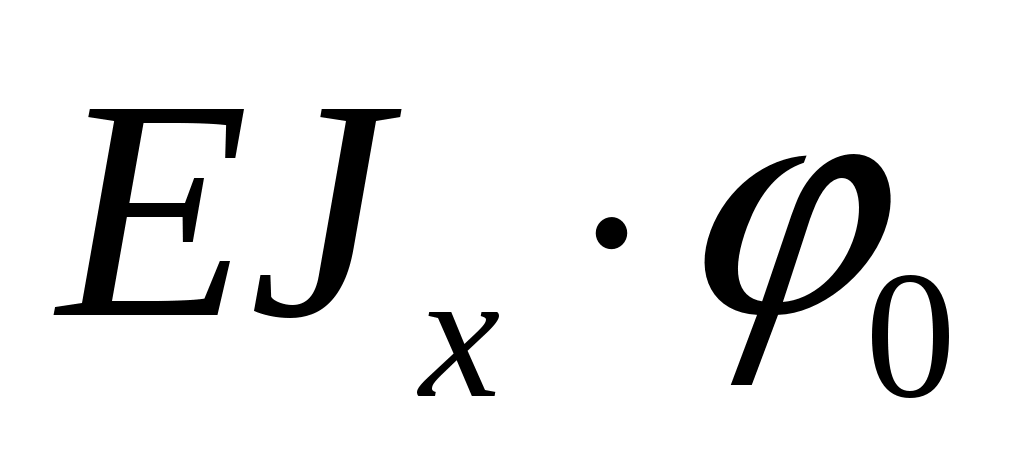 :
:
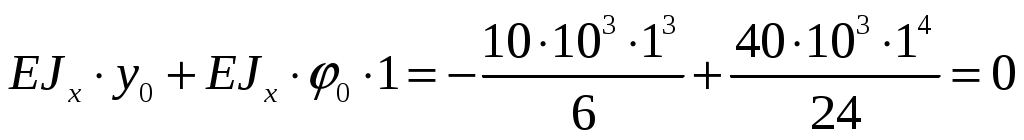 ;
;
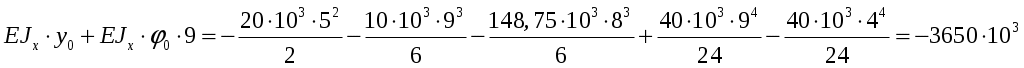
Решаем систему уравнении где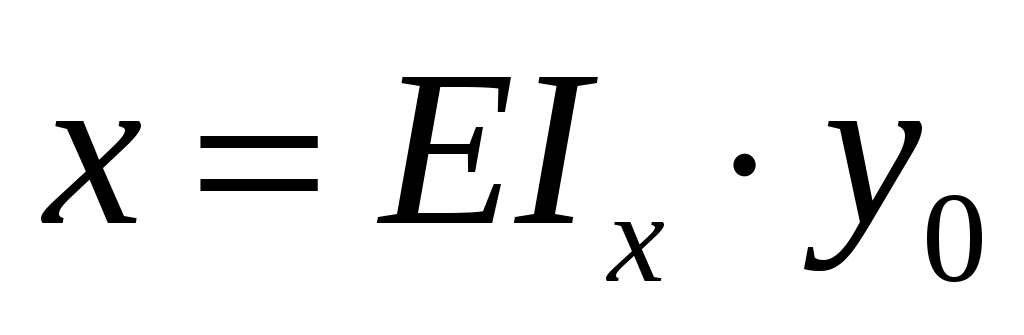 ;
; 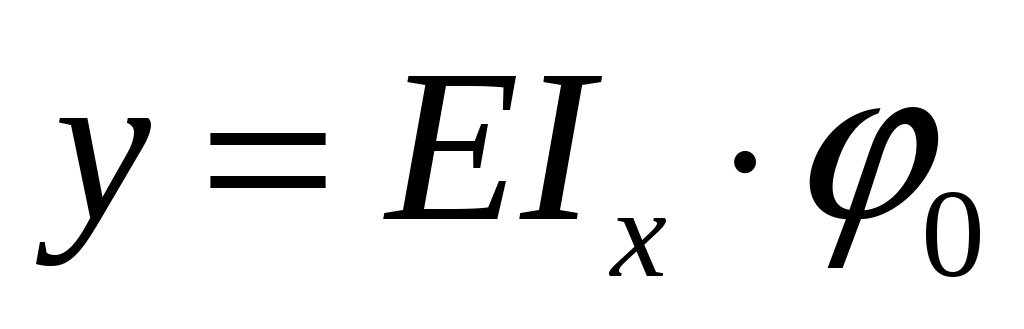 :
:
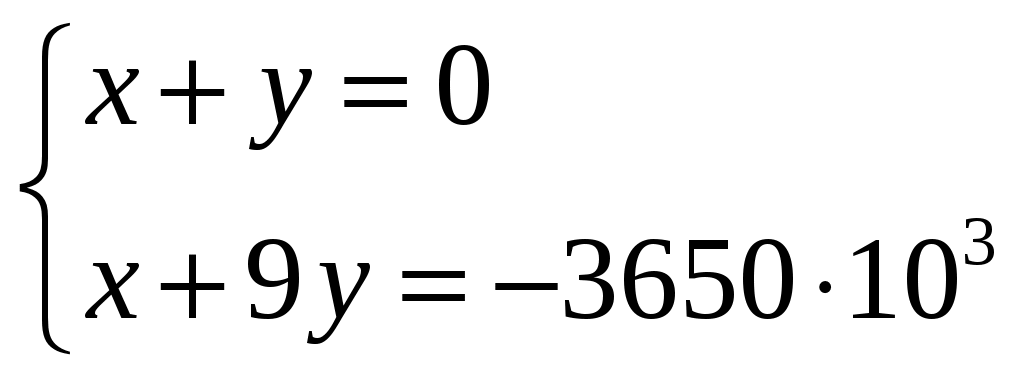

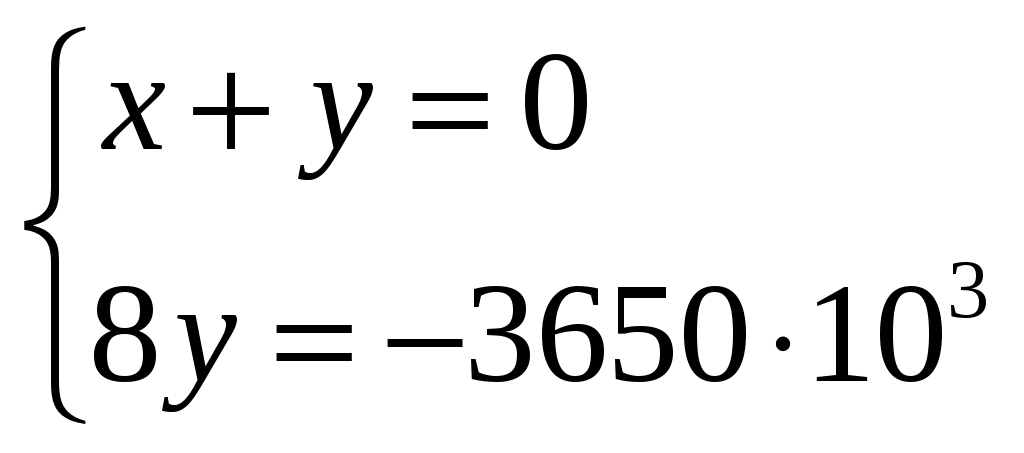

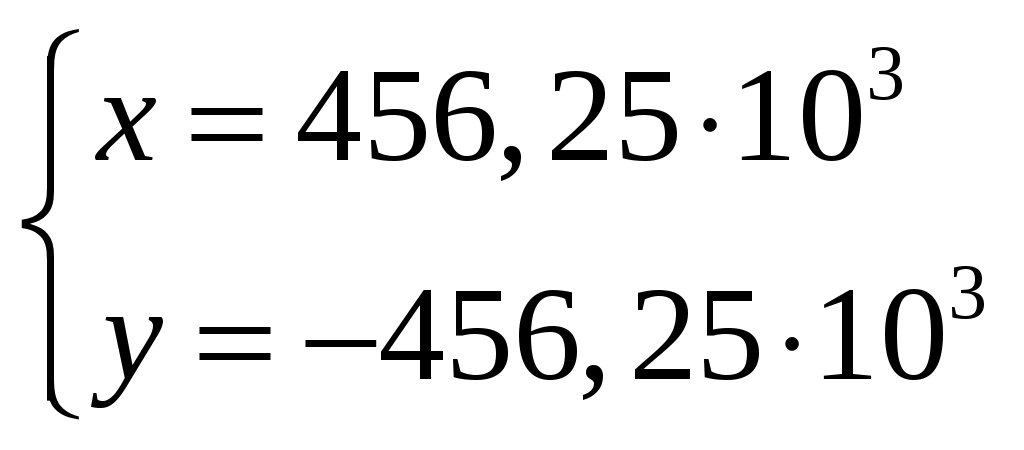
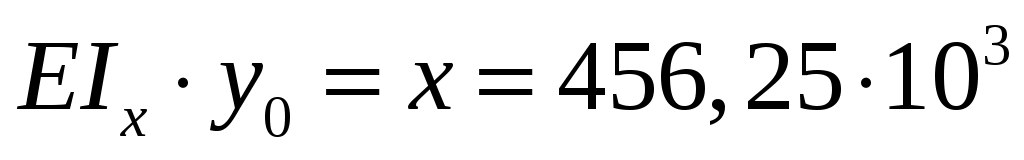 ;
;
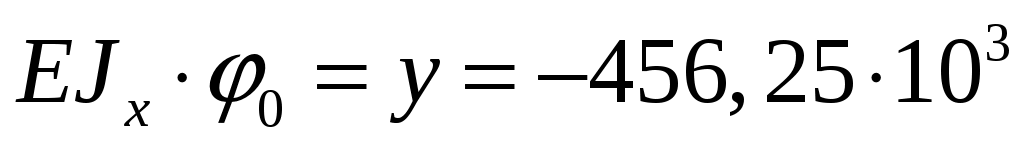
Окончательно общее уравнение примет следующий вид:
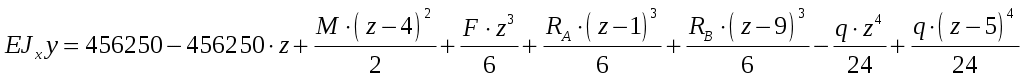 .
.
Подставляя соответствующие значения
Определяем диаметр первой ступени из условия жесткости:
где
Тогда
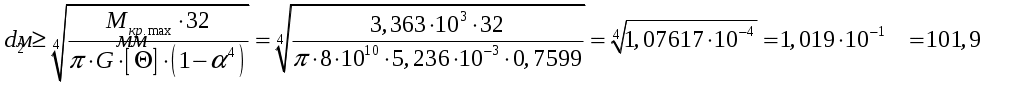 .
.Принимаем
2. Определив размеры сечений бруса, строим эпюры максимальных касательных напряжений и абсолютных углов закручивания (рис. 7.4, в, г).
На первом участке:
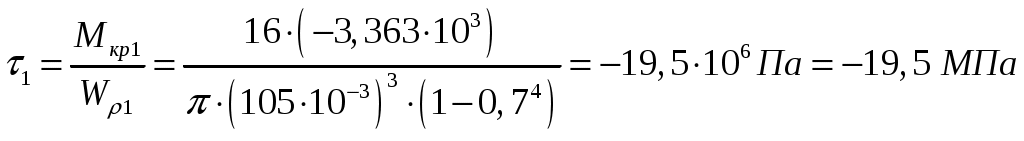 ;
;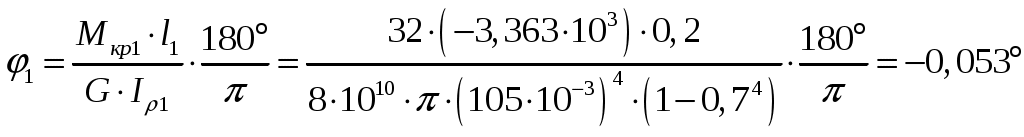 .
.На втором участке:
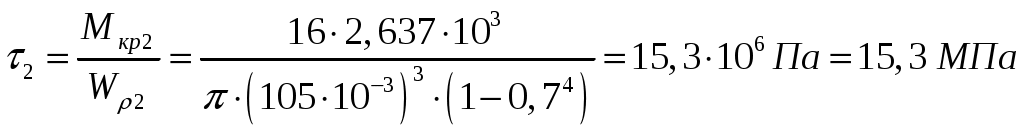 ;
;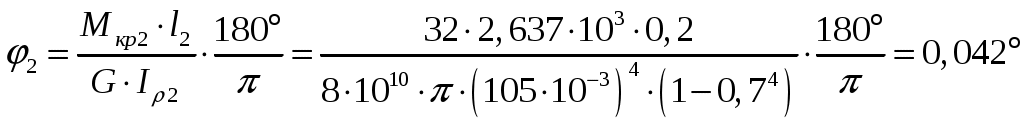 .
.На третьем участке:
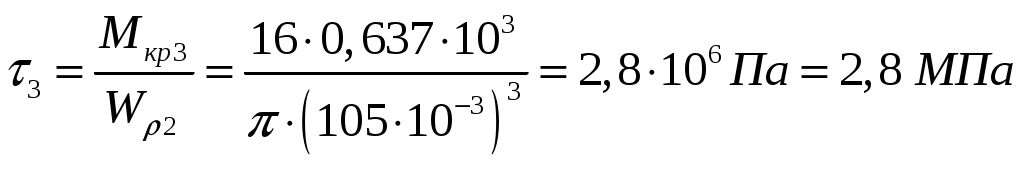 ;
;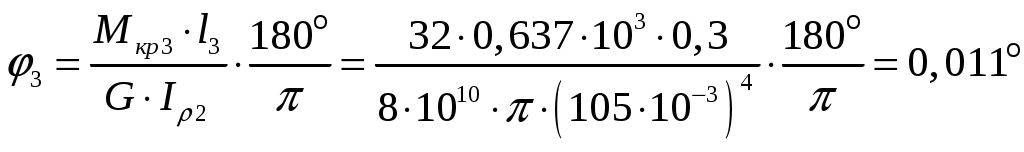 .
.Проверяем угол закручивания на правом конце балки:
Угол закручивания правого конца балки равен нулю, следовательно, задача решена правильно.
3. Сравниваем максимальное касательное напряжение с допускаемым касательным напряжением:
4. Определяем рабочий максимальный относительный угол закручивания и сравниваем его с допускаемым.
На всех участках стержня выполняются как условия прочности, так и условие жесткости. Значительно меньшее рабочее касательное напряжение получилось вследствие того, что окончательные размеры сечений были приняты из расчета на жесткость.

Рис. 7.4. Эпюры.
Задача № 8
Для заданной балки (рис.8.1) по исходным данным требуется:
1) построить расчетную схему балки в выбранном масштабе;
2) построить эпюры поперечных сил и изгибающих моментов;
3) из условия прочности при изгибе определить номер профиля двутавровой балки в соответствии с ГОСТ 8239-89, приняв допускаемое нормальное напряжение равным
4) построить эпюру перемещений сечений балки.
Исходные данные:

Рис. 8.1. Двухопорная балка.
Решение:
1. Освобождаем балку от связей и заменяем действие связей силами реакций
Из уравнения (1) находим:
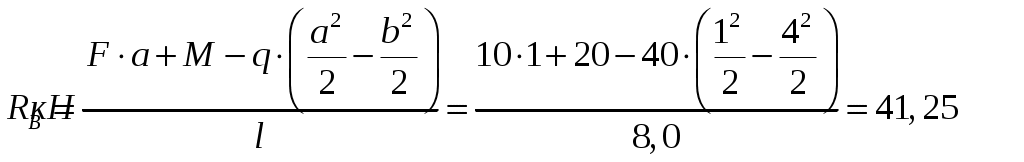 .
.Из уравнения (2) находим:
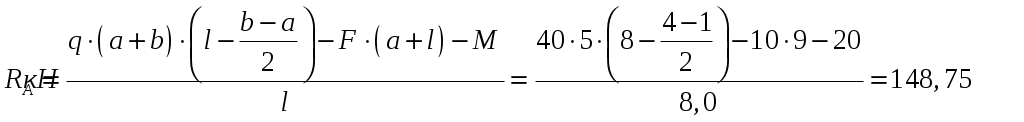 .
.Проверка:
Следовательно, реакции связей определены верно.
2. Разбиваем балку на силовые участки.
Анализ внутренних силовых факторов:
На первом участке
;
Эпюра
На втором участке
Эпюра
На третьем участке
;
Эпюра
На четвертом участке
Эпюры поперечных сил и изгибающих моментов приведены на рис. 8.2, б, в. Из построенных эпюр видно, что максимальный изгибающий момент равен
3. Из условия прочности по нормальным напряжениям подбираем сечение:
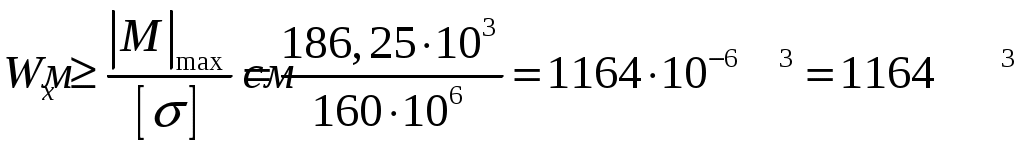 .
.По ГОСТ 8239-89 ближайший номер двутавра № 45 с
4. Для балки с принятыми размерами определим перемещения сечений по универсальному уравнению изогнутой оси линии. Выберем начало координат в левом крайнем сечении (точка приложения силы

Рис. 8.2. Эпюры
,
В этом уравнении два неизвестных постоянных интегрирования
Решая совместно уравнения (4) и (5), находим значения
Решаем систему уравнении где
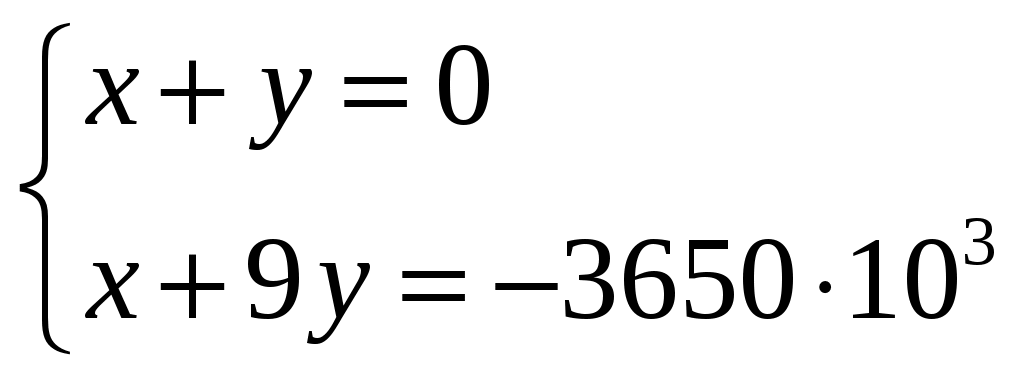
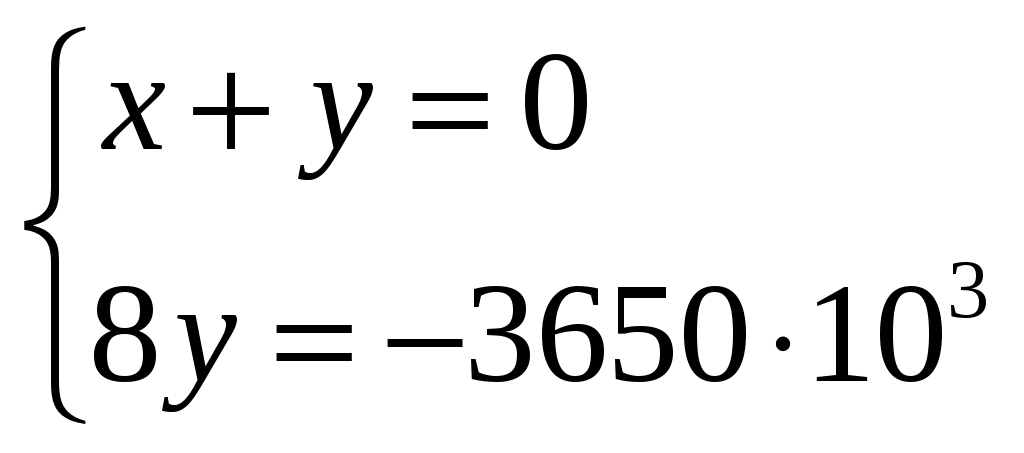
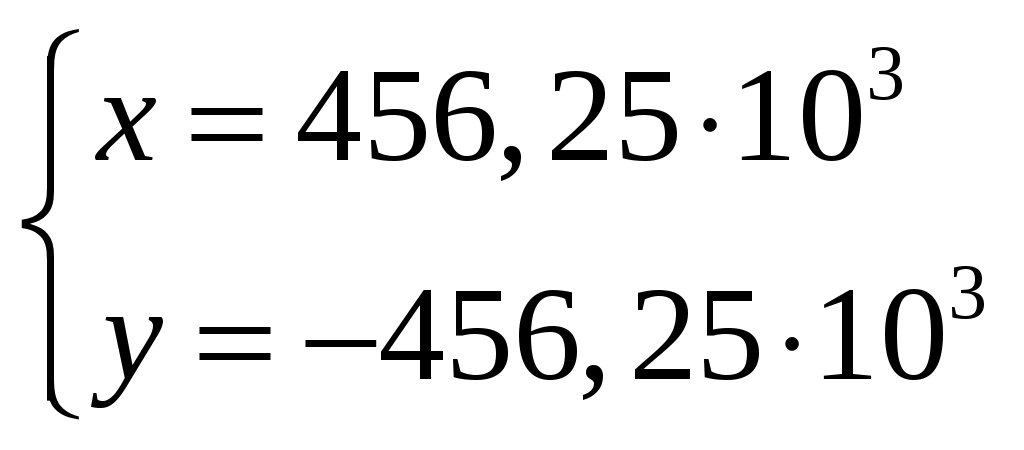
Окончательно общее уравнение примет следующий вид:
Подставляя соответствующие значения