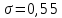Добавлен: 07.11.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «ВГТУ», ВГТУ)
Радиотехники и Электроники
(факультет)
Кафедра радиоэлектронных устройств и систем
Отчёт по лабораторной работе №2
по дисциплине «Статистическая радиотехника»
Тема «Энергетические характеристики случайных процессов»
Выполнил студент группы РП-201_______________________________Гуров М.И._
Подпись, дата Инициалы, фамилия
Выполнил студент группы РП-201___________________________Шероухов К.С._
Подпись, дата Инициалы, фамилия
Проверил ______________________________Токарев А. Б._
Подпись, дата Инициалы, фамилия
Защищена ____________________ Оценка _____________________________
«Вероятностные характеристики случайных процессов»
Вариант НБ=25
Цель работы – экспериментальное исследование энергетических (корреляционных и спектральных) характеристик СП
В работе изучаются основные свойства функции распределения вероятностей и плотности вероятностей СП – шума, периодической последовательности импульсов и смеси сигнала с шумом. Для разных типов процессов измеряются математическое ожидание и дисперсия, анализируются взаимосвязи числовых и вероятностных характеристик, исследуется влияние шумов на сигналы.
Домашнее задание к лабораторной работе
Номер бригады НБ=25, а также параметр ГП=0.
Для своего варианта рассчитаем графики СПМ и корреляционной функции шума.
Таблица 1 – Параметры шума
| НБ | Тип шума: ограничен по… | Максимальное значение СПМ S0, В2/Гц | Частотные ограничения, кГц |
| 25 | Частоте | 22∙10-5 | FMAX=5.5 |
СПМ SОЧ(f)=S0, при |f| < FMAX,
Корреляционная функция BОЧ(τ)=2∙S0 ∙FMAX ∙ sinc(2∙π∙FMAX∙τ),
Дисперсия DОЧ=2 ∙ S0∙ FMAX.
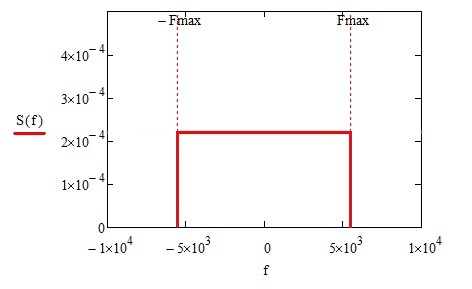
Рисунок 1 – СПМ шума, ограниченного по частоте
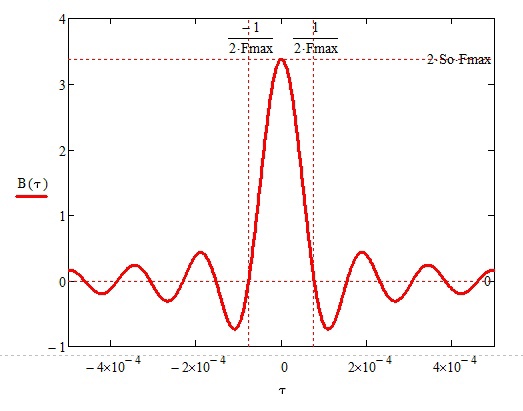
Рисунок 2 – Корреляционная функция шума, ограниченного по частоте
Таблица 2 – Данные квазислучайного сигнала
| НБ | Вид формируемого сигнала | Параметры сигнала |
| 25 | Прямоугольный | Um=Amax, F=2 кГц |
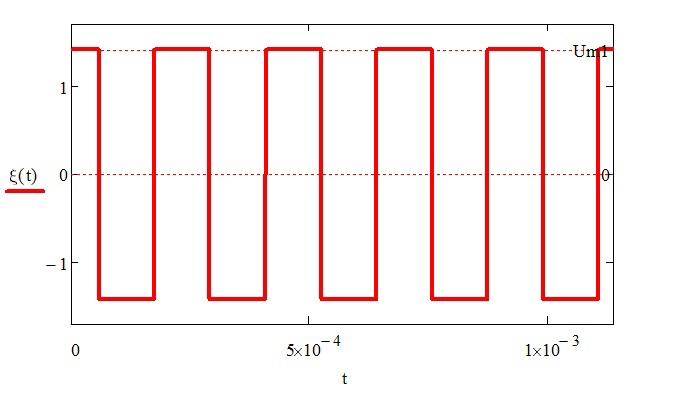
Рисунок 3 – График гармонического сигнала
Необходимо рассчитать амплитуду сигнала AMAX, обеспечивающую отношение сигнал-шум по напряжению h=2, и амплитуду сигнала AMIN, обеспечивающую отношение сигнал-шум h=0.2. Для каждой из найденных амплитуд построим графики корреляционных функций и СПМ аддитивной смеси сигнала и шума.
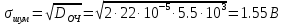
При
, 
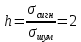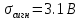. Т.к. сигнал прямоугольный, то 
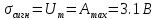.При
, 
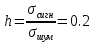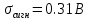. Т.к. сигнал прямоугольный, то 
.Используем примечание: при построении энергетических характеристик смеси сигнала и шума следует иметь в виду, что для некоррелированных СП корреляционная функция суммы равна сумме корреляционных функций слагаемых. Аналогичное утверждение справедливо и для спектральной плотности процессов.
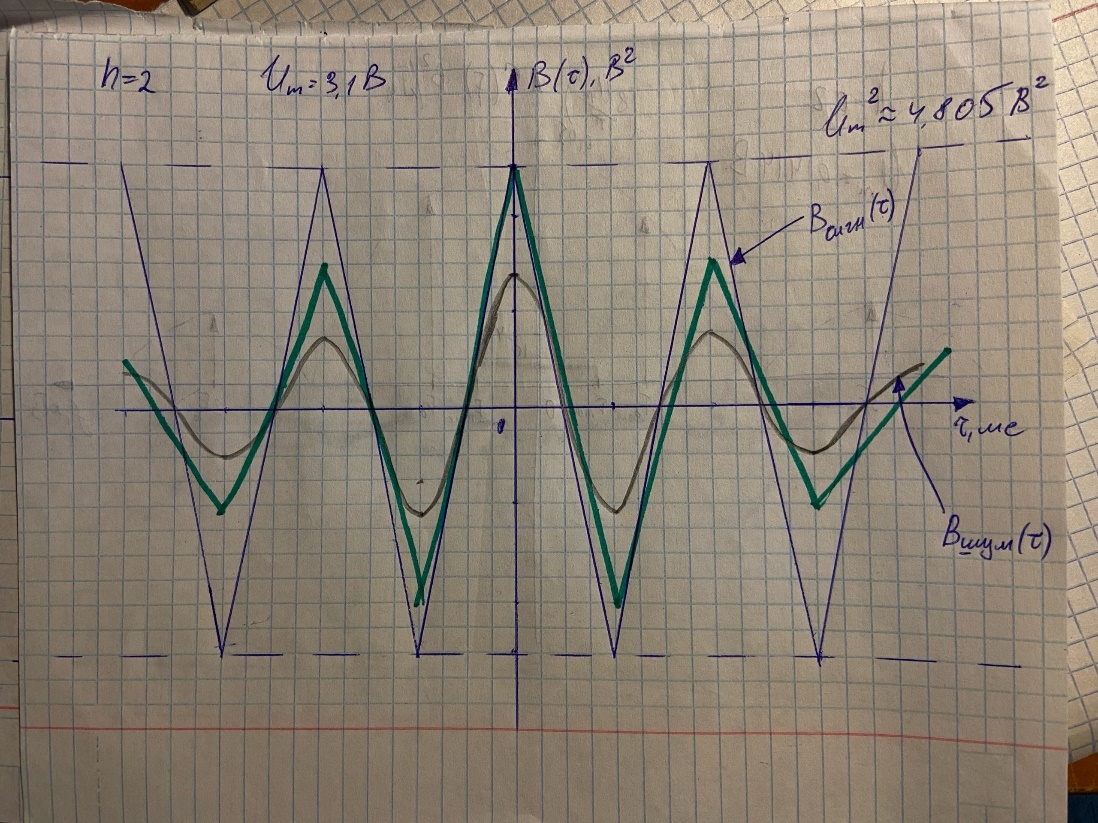
Рисунок 4 – Корреляционная функция смеси при h=2
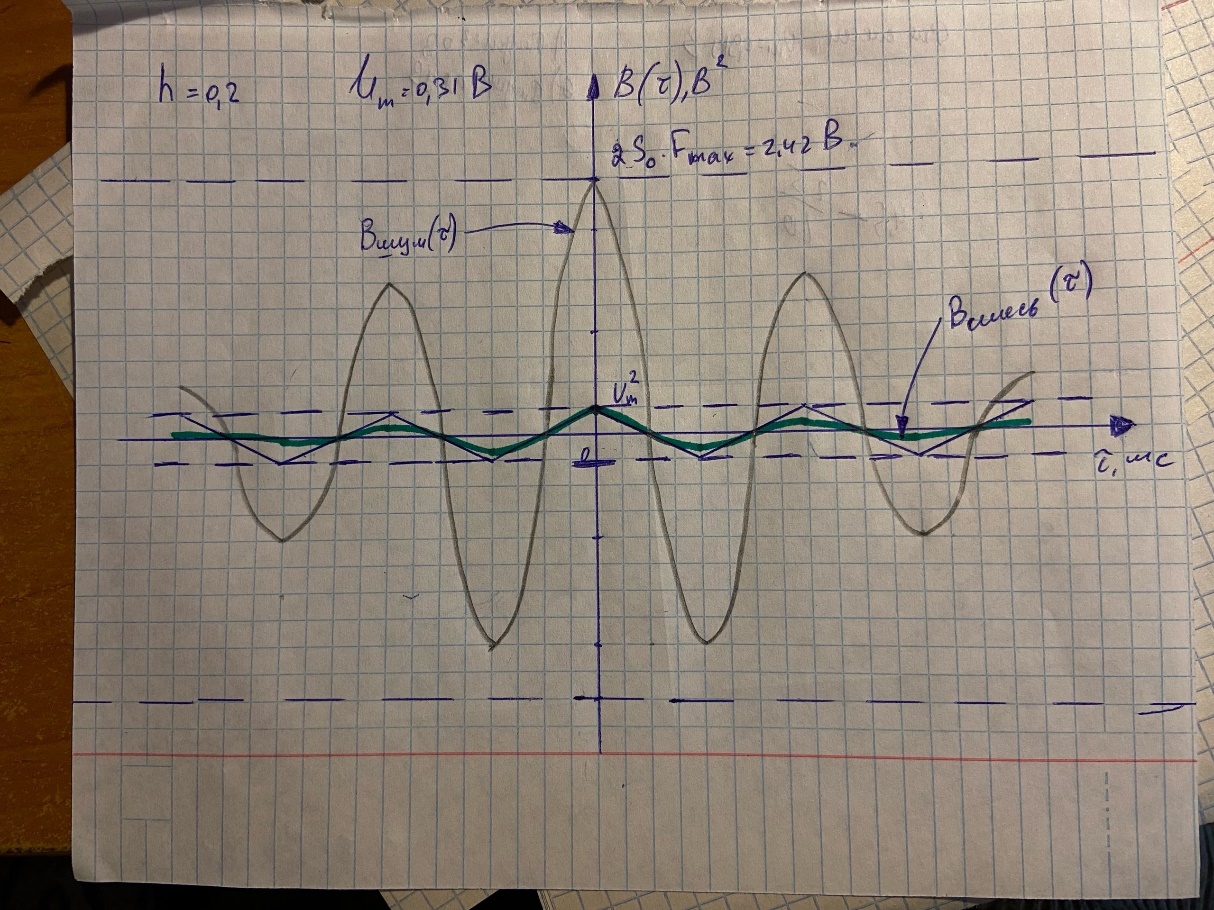
Рисунок 5 - Корреляционная функция смеси при h=0.2
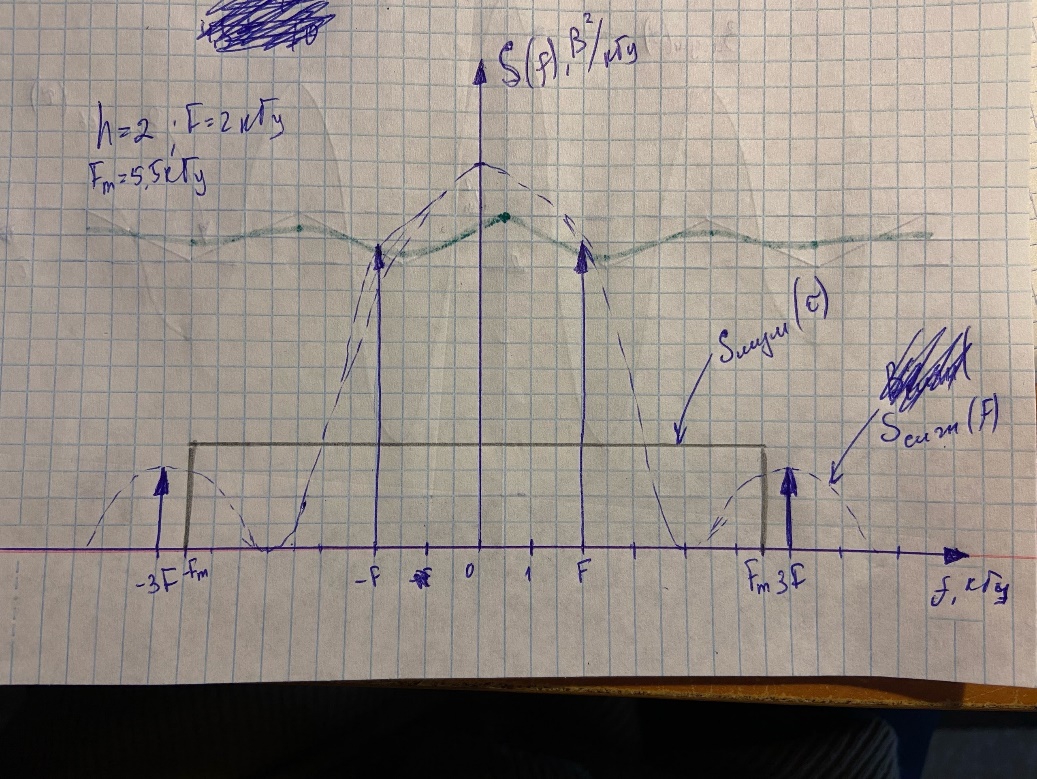
Рисунок 6 – СПМ смеси при h=2
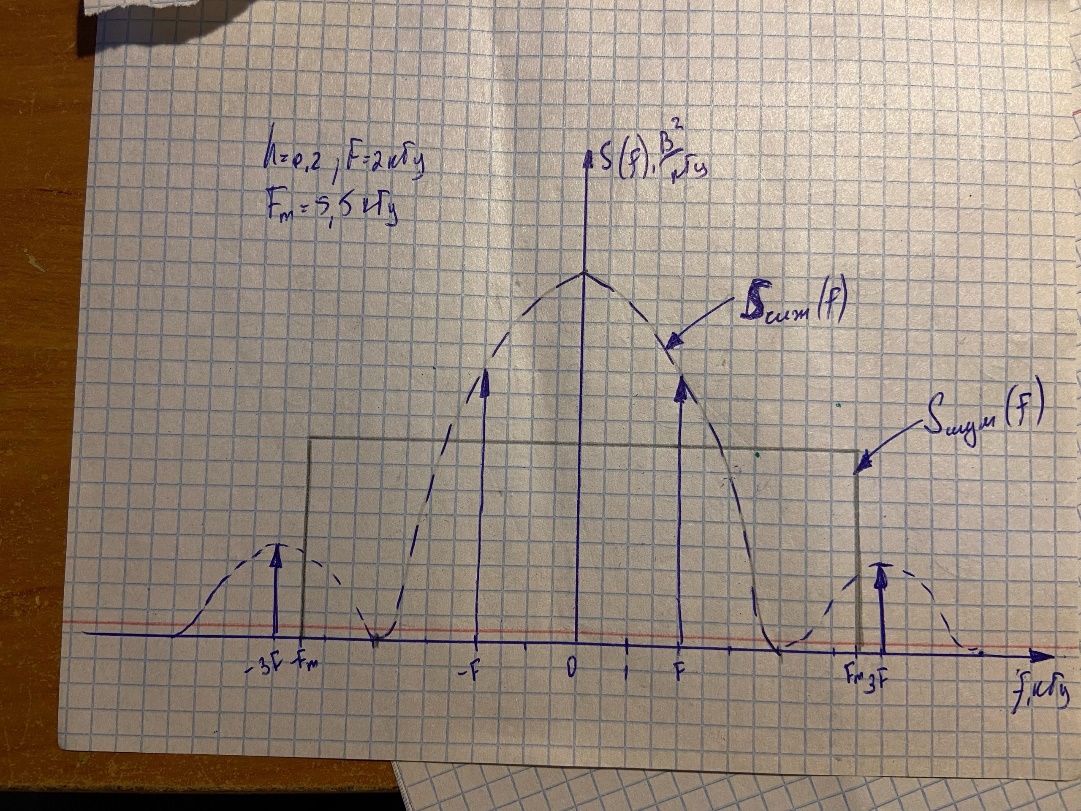
Рисунок 7 – СПМ смеси при h=0.2
2. Выполнение лабораторных исследований
Этап 1. Исследование Энергетических характеристик шума
Устанавливается тип и параметры модуля №1, в соответствии с вариантом 1, схемы моделирования случайных процессов на формирование шума с эффективным значением
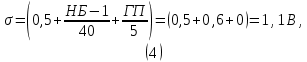
Тип шума и прочие параметры модуля №1 устанавливаются в соответствии с вариантов 25 - источник шума – низкочастотный, с дополнительным параметром
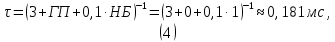
Остальные модули переводятся в выключенное состояние. Объем формируемой выборки N = 4096 отсчетов. Частота дискретизации
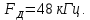В блоке анализаторов оба анализатора настраиваются на контрольную точку №1; устанавливается левый анализатор в состояние осциллографа, а правый – коррелометра.Формируя новые реализации СП путем нажатия кнопки "Обновить данные", проводится серия из 15 экспериментов. По полученным графикам производится анализ стабильности корреляционной функции. Результат моделирования представлен на рисунке 5.
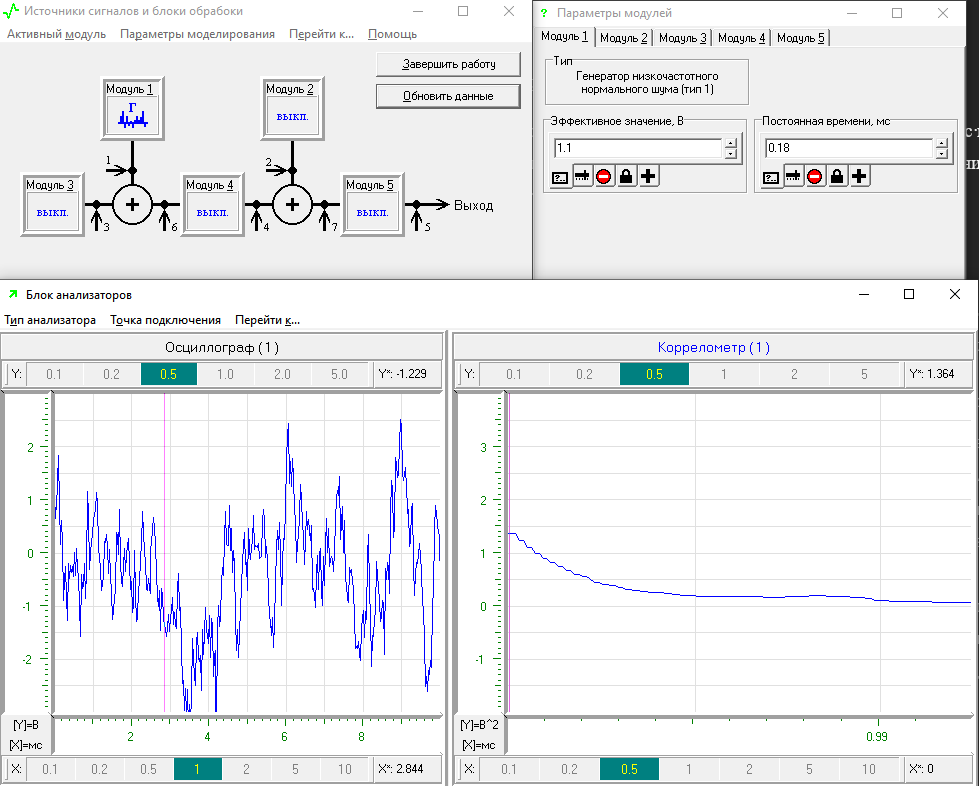
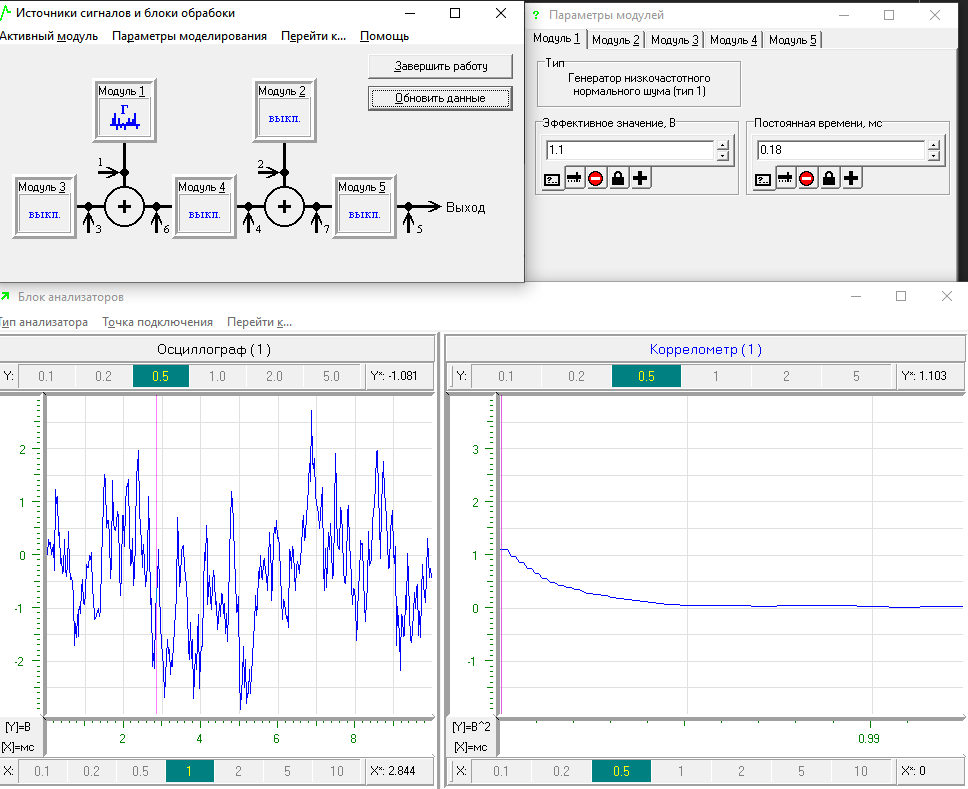
Рисунок 5 – Наблюдаемая корреляционная функция
Из графиков на рисунке 5 можно сделать вывод, что корреляционная функция стабильна.
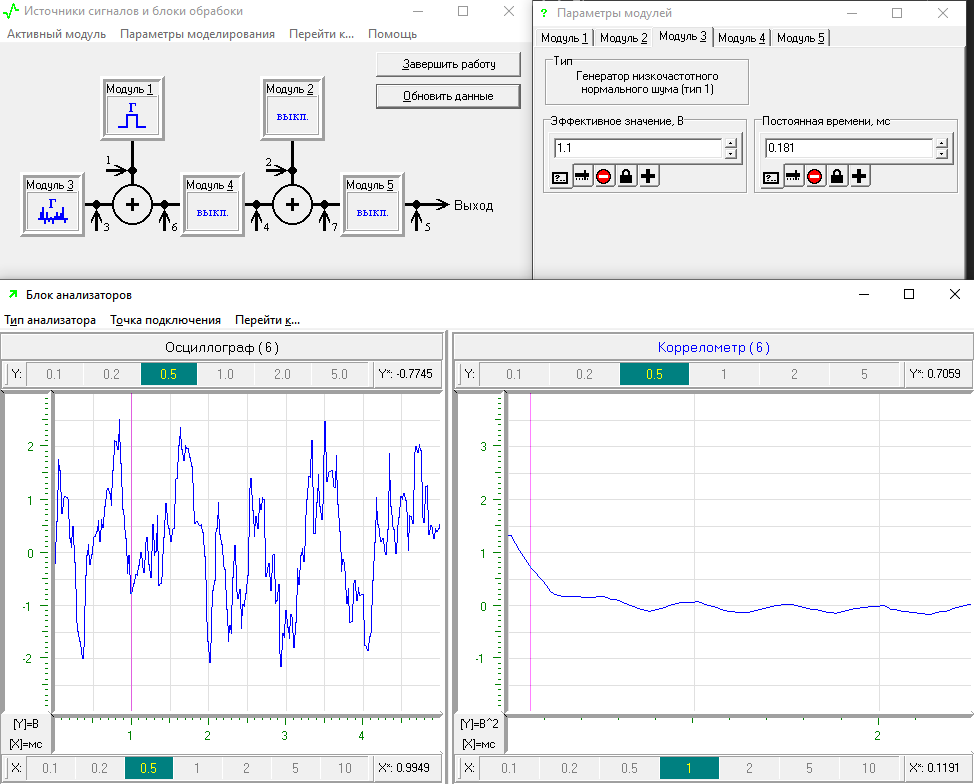
Далее, правый анализатор переключается в состояние спектроанализаторана, и также проводится серия из 15 экспериментов. Результат приведен на рисунке 6.
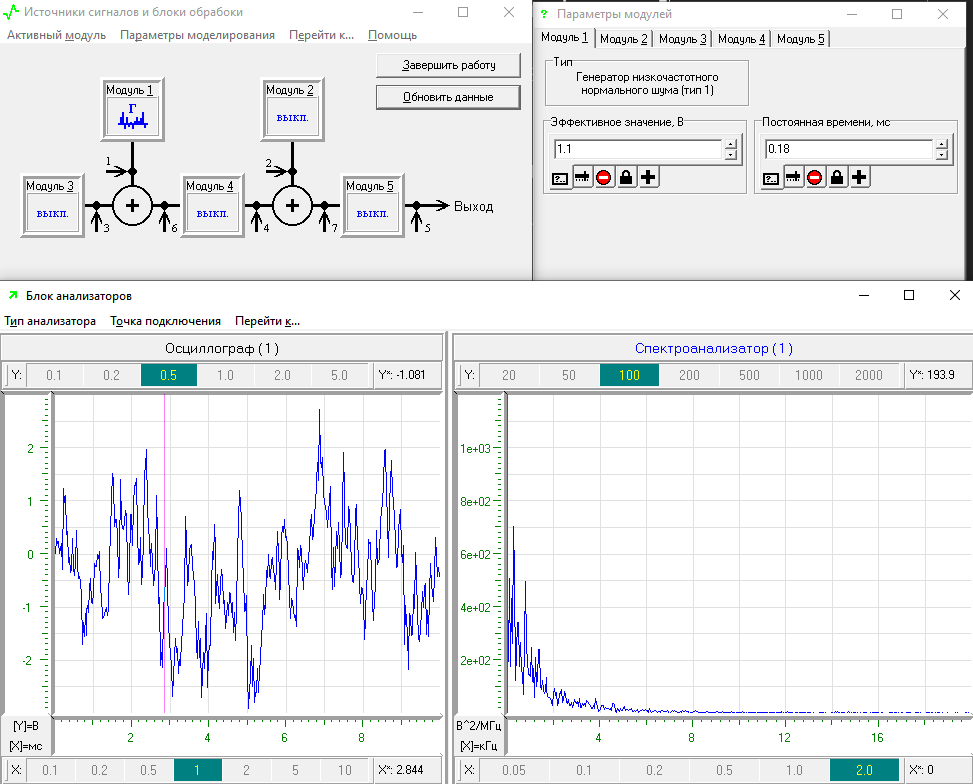
Рисунок 6 – Оценка спектральной плотности мощности
Из графика на рисунке 6 можно сказать, что в отличие от корреляционной функции оценка спектральной плотности мощности даже при большой длительности выборки оказывается весьма неустойчивой.
При сравнении с теоретическими расчетами выявлены отличия энергетических характеристик СП.
Этап 2. Исследование энергетических характеристик квазислучайных процессов
Установить тип и параметры модуля №1 моделирующей программы в соответствии с вариантом 25 (вид формируемого сигнала – прямоугольный, параметры сигнала –
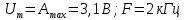). После чего проводится исследование оценки спектральной плотности мощности СП. Результат моделирование представлен на рисунке 7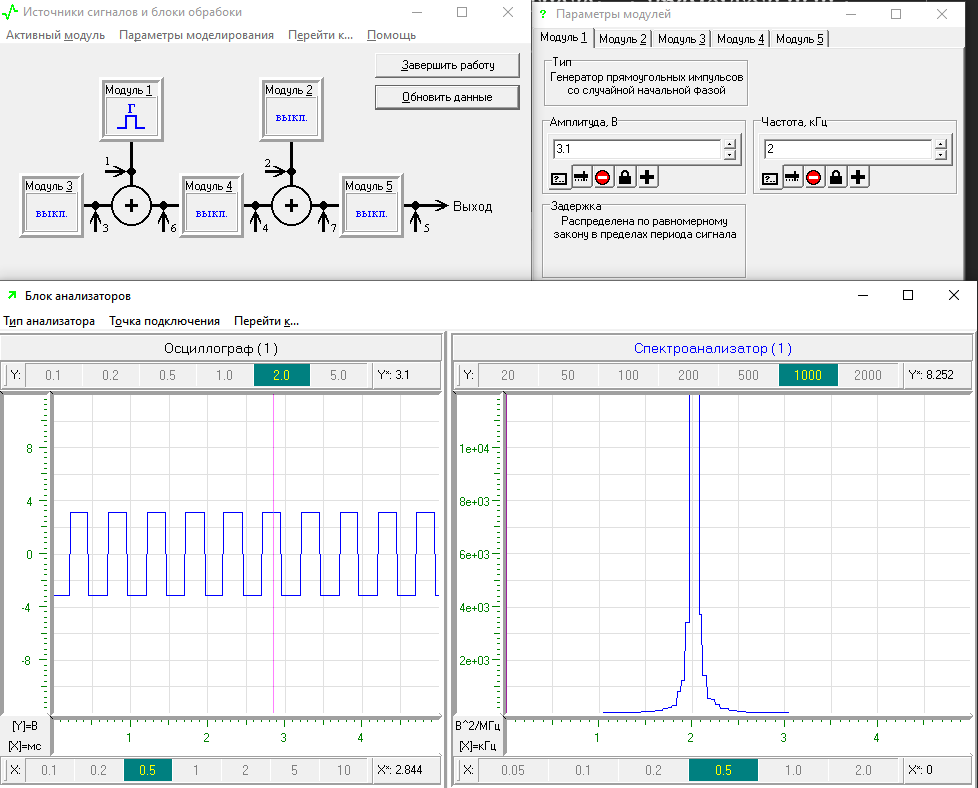
Рисунок 7 – Спектральной плотность мощности реализации СП
Из графиков на рисунке 7 можно сделать вывод, что ценка спектральной плотности мощности СП стабильна.
Дале, левый анализатор переключается в режим оценки числовых характеристик СП, а правый анализатор – в состояние коррелометра, после чего проводится серия из 15 экспериментов. Результат моделирования представлен на рисунке 8.
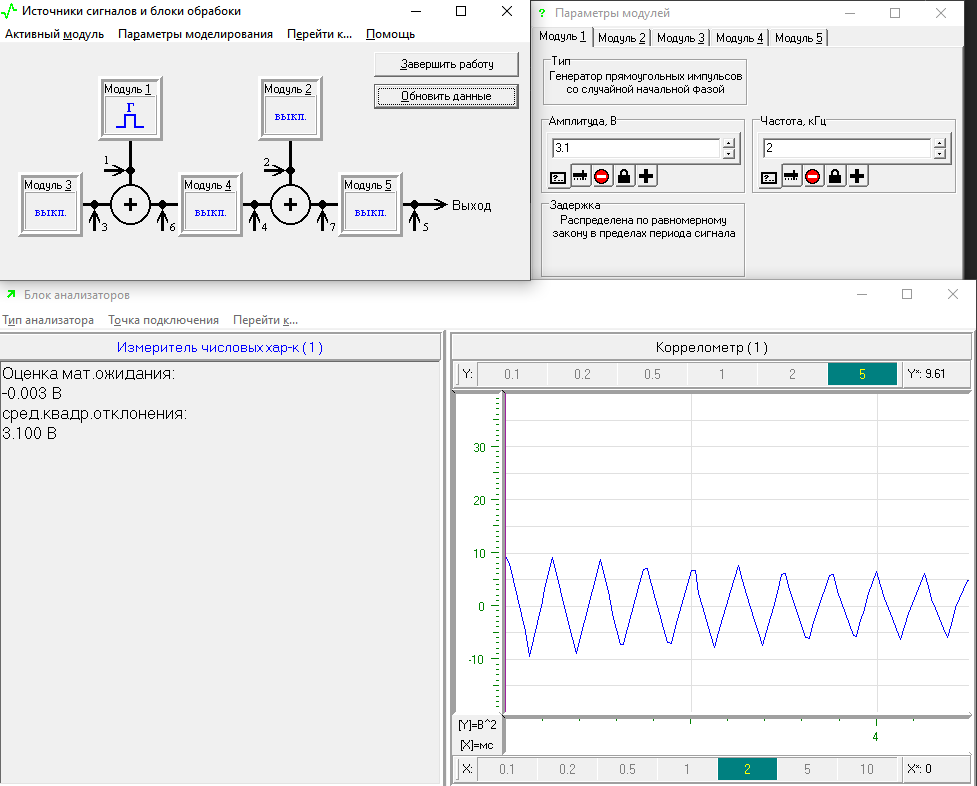
Рисунок 8 – Корреляционная функция реализаций СП
После этого, объём выборки устанавливается на значение N = 512 отсчётов, а затем проводится серия из 15 экспериментов. Результат моделирования представлен на рисунке 9.
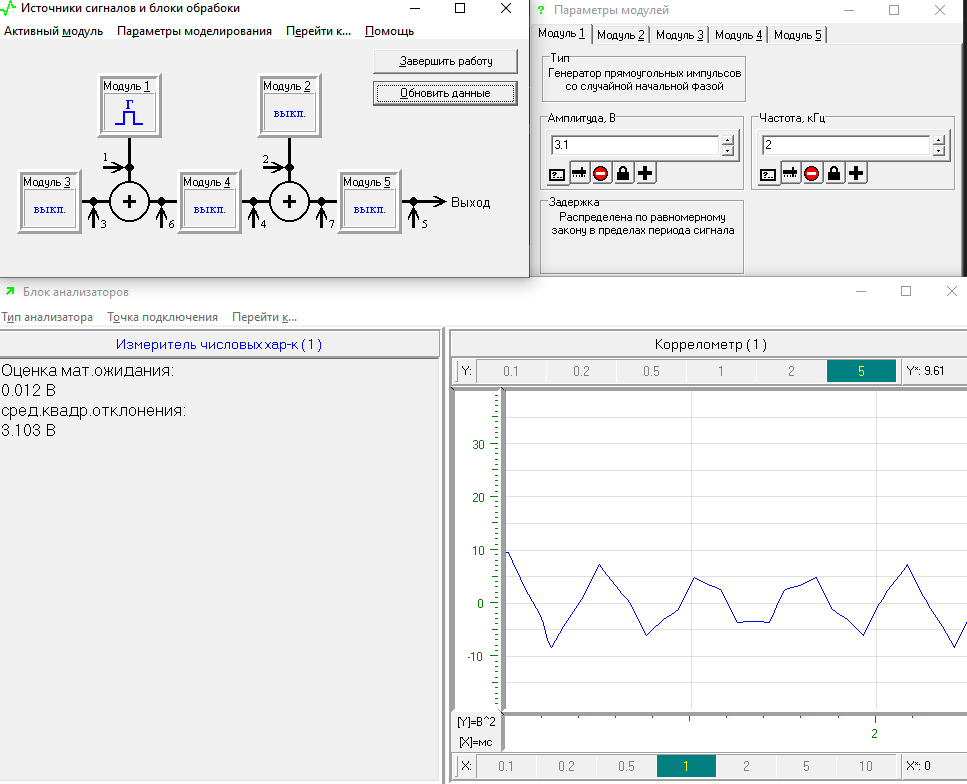
Рисунок 9- Влияние объёма выборки N на результат наблюдаемых оценок
Далее, объём выборки снова устанавливается на значение N = 4096 отсчётов, оба анализатора на выход первого сумматора переключается на контрольную точку №6, а модуль №3 схема моделирования переводится в режим формирования постоянной составляющей с величиной, равной
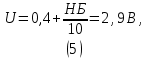
И проводится аналогичному ранее исследование, где левый анализатор переключается в режим оценки числовых характеристик СП, а правый анализатор – в состояние коррелометра, после чего проводится серия из 15 экспериментов. Результат моделирования представлен на рисунке 10.
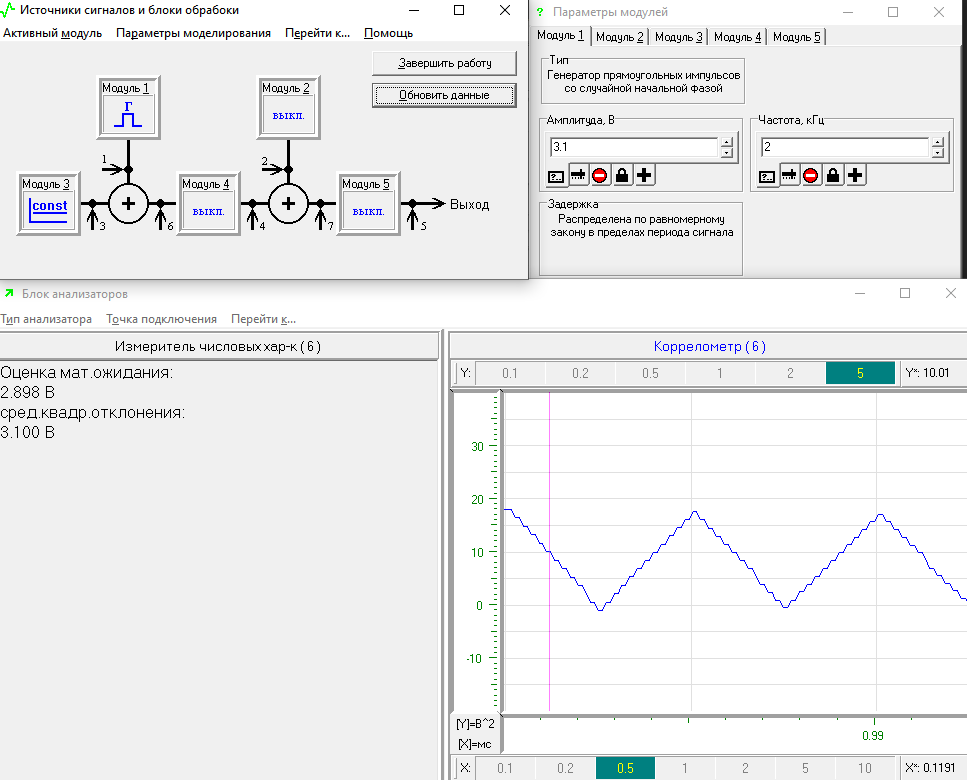
Рисунок 10 - Влияние постоянной составляющей на результат наблюдаемых оценок
Этап 3. Исследование влияния аддитивного шума на вероятностные характеристики СП.
В соответствии с вариантом 25 настраивается модуль №1 схемы моделирования на формирование сигнала (вид формируемого сигнала – прямоугольный, параметры сигнала –
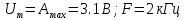), а модуль №3 на формирование шума (источник шума – низкочастотный, 
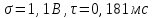). Анализаторы устанавливаются в режим осциллографа и коррелометра
, настраиваются на выход сумматора, т.е. на контрольную точку №6. Результат моделирования представлен на рисунке 11.
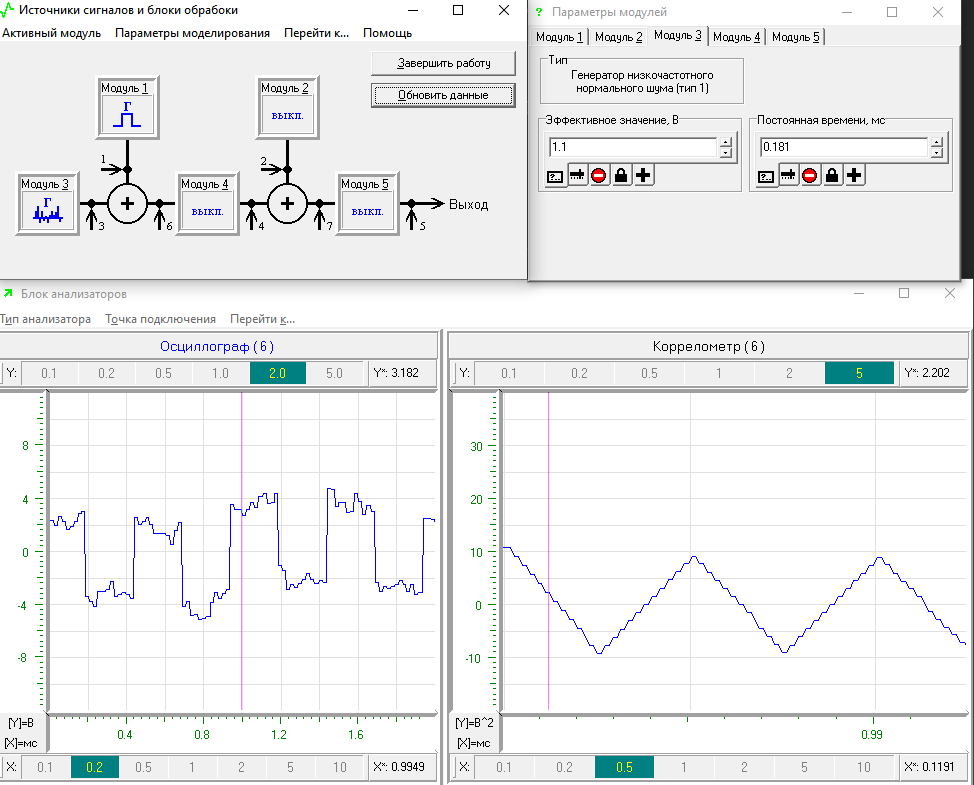
Рисунок 11 – Типовая корреляционная функция смеси сигнала и шума
Далее, необходимо повторить исследование изменив амплитуду сигнала, формируемого модулем №1, на величину
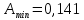. Результат моделирования представлен на рисунке 12.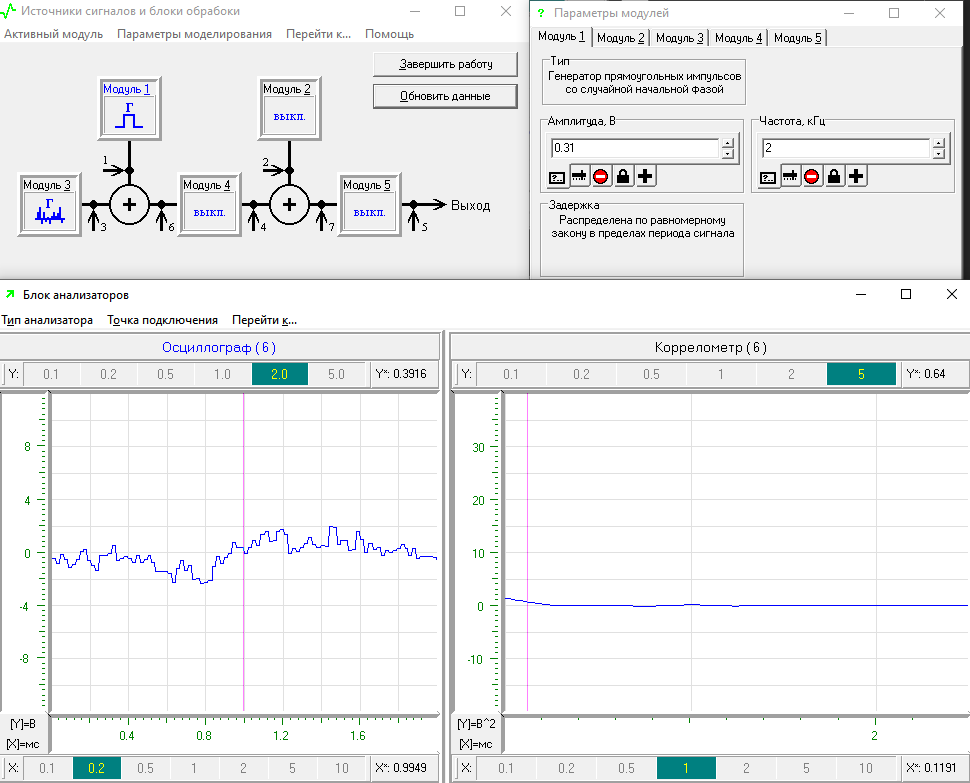
Рисунок 12 – Типовая корреляционная функция смеси сигнала и шума при амплитуда равной
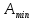
После этого, нужно в окне программы «Параметры модулей» открыть вкладку «Модуль 3», контролирую параметры формируемого схемой моделирования шума. Осуществляя ручную корректировку уровня шума в пределах от
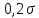до 
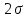(где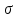 
определяется вариантом 25), проследить за изменением оценок корреляционной функции СП, обращая внимание на разницу в поведении этих функций при значениях аргумента 
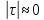и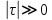 
. Результаты моделирования представлены на рисунке 13, 14,15 и 16.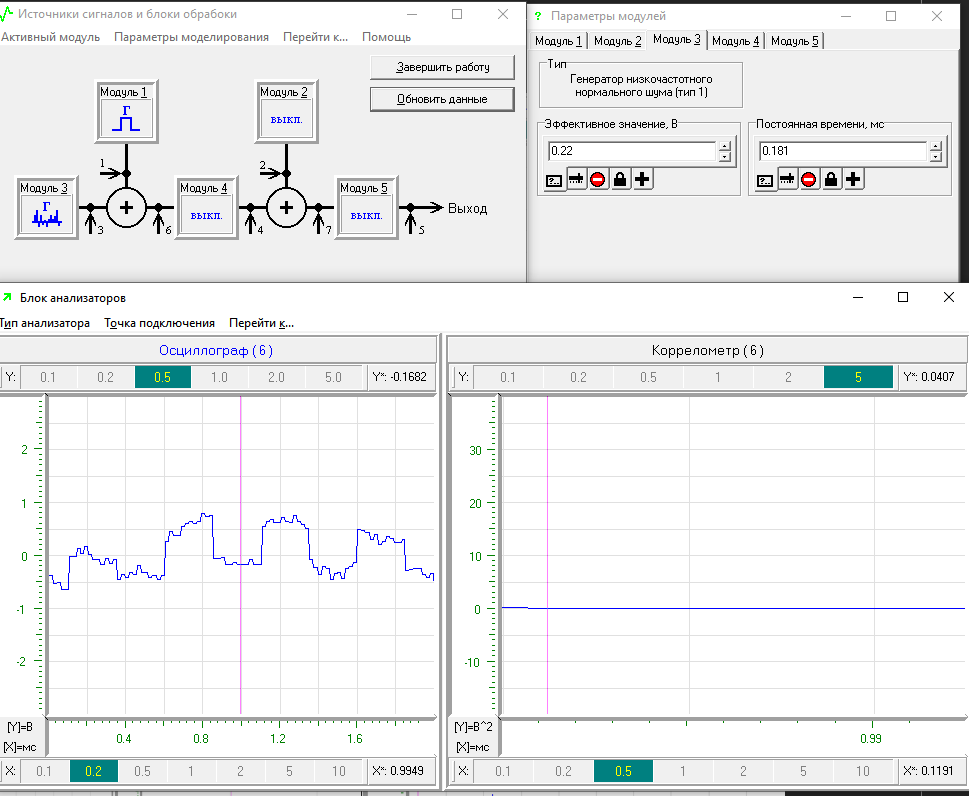
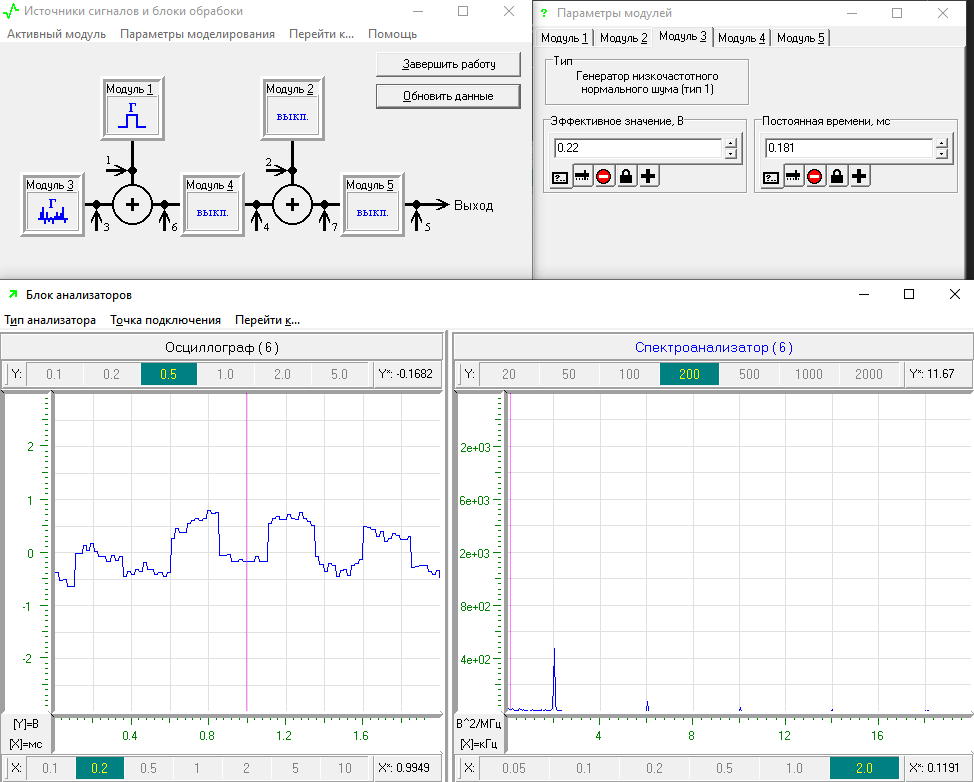
Рисунок 13 – Корреляционная характеристика и спектральная плотность мощности при уровне шума
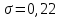
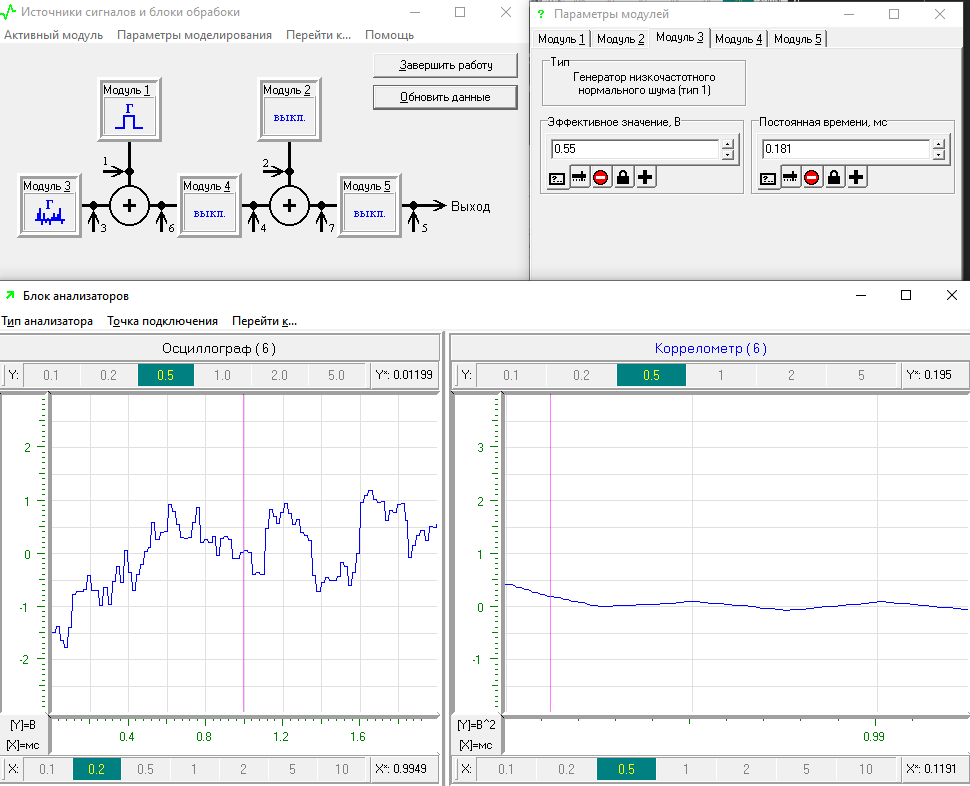
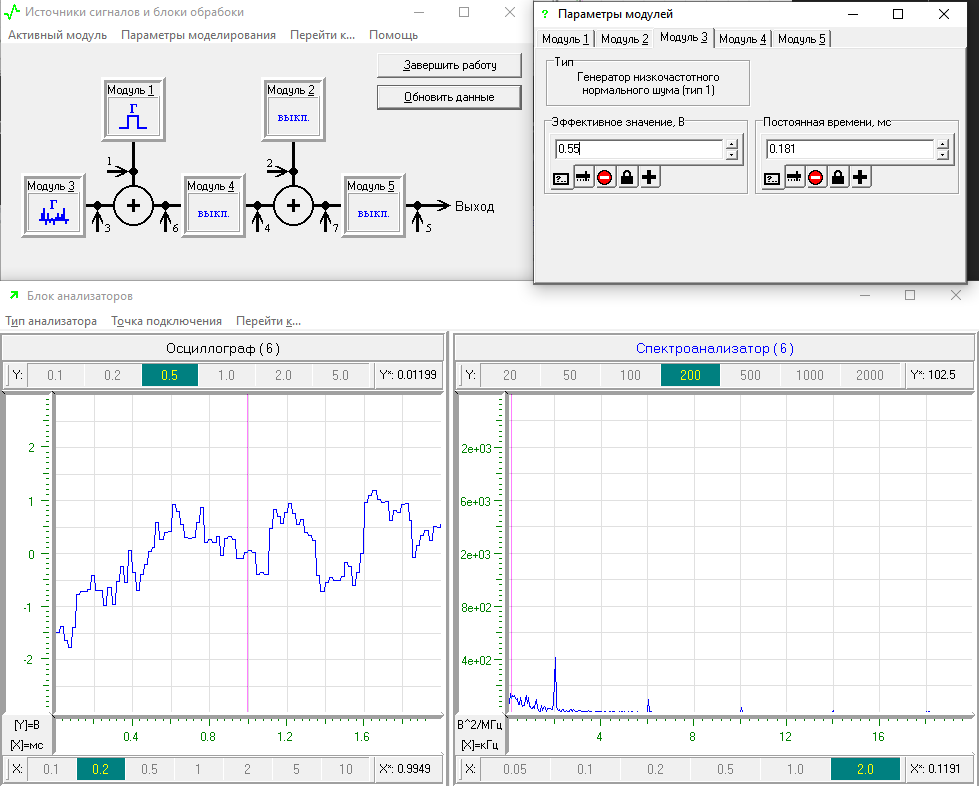
Рисунок 14 – Корреляционная характеристика и спектральная плотность мощности при уровне шума
