Автономная некоммерческая организация высшего образования
«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»
|
Кафедра экономики и управления
Форма обучения: заочная/очно-заочная
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКАГруппа
М20М661СтудентПантелеева Алена ОлеговнаМОСКВА 2023Задача 1.Буквы, составляющие слово РАКЕТА, написаны по одной на шестикарточках; карточки перемешаны и положены в пакет.1.1. Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМслово РЕКА?1.2. Какова вероятность сложить слово КАРЕТА при вынимании всех букв?Решение:1.1.Количество событий = общему количеству букв = 6.Из них благоприятных событий (подходящих букв) = 1.Вероятность по формуле Лапласа:Р = 1 / 6.Вероятность, что вторая буква Е:Р = 1/5 (из оставшихся 5ти букв 1 Е);Вероятность того, что третья буква будет К:Р = 1/4 (из оставшихся 4х букв 1 К);Вероятность того, что четвертая буква будет А:Р = 2/3 (из оставшихся 3х букв 2 А);Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А: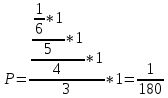1.2 6 карточек: "ААЕКРТ". Берем первую карту. С вероятностью 1/6 вытащили "К". Осталось 5 карт "ААЕКТ". Берем вторую. С вероятностью 2/5 вытаскиваем "А". Осталось 4 карты "АЕКТ". 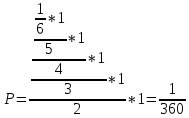С вероятностью 1/4 вытаскиваем "Р", потом с вероятностью 1/3 - "Е", 1/2 - "Т", 1 - "А".Ответ:1.1. 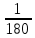; 1.2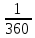
Задача 2. Дискретная случайная величина Ƹ задана следующим закономраспределения:
Ƹ
|
4
|
6
|
10
|
12
|
р
|
0,4
|
0,1
|
0,2
|
0,3
|
Найти математическое ожидание, дисперсию и среднее квадратическоеотклонение.M = 4*0,4 + 6*0,1 + 10*0,2 + 12*0,3 = 738D = 16*0,4 + 36*0,1 + 100*0,2 + 144*0,3 = 73,2СКО = sqr(73,2) = 8,55Ответ: 7,8; 73,2; 8,55.Задача 3. Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание М(Ƹ) = 1.9, а такжеМ( 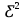) = 7,3, найти вероятности 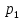, ,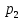 , 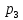которые соответствуютдискретным значениям случайной величины.Решение:
Дисперсия случайной величины Х: 
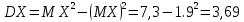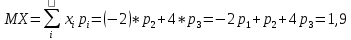
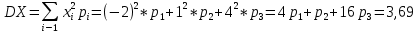
. Поскольку Х-дискретная, тоУчитываем условие, что + +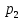 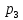=1 Решаем как систему уравнений: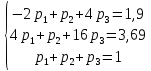
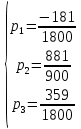
Но значение вероятности 
,
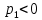что неверно. Поэтому задача решений не имеет.