Представление чисел с плавающей точкойЭта статья находится в разработке!

Содержание  [убрать]  1Плавающая точка 2Нормальная и нормализованная формы 3Числа двойной точности 4Свойства чисел с плавающей точкой 5Особые значения чисел с плавающей точкой 5.1Ноль (со знаком) 5.2Бесконечность (со знаком) 5.3Неопределенность 5.4Денормализованные числа 6Машинная эпсилон 7Unit in the last place (Unit of least precision) 8Погрешность предиката "левый поворот" 8.1Определения 8.2Расчет 8.3Ответ 9Ссылки

[править]Плавающая точка

Определение:

Плавающая точка (floating point) - метод представления действительных чисел, при котором число хранится в виде мантиссы и показателя степени, а значение числа вычисляется по формуле:  , где   - число,   - бит, отвечающий за знак числа,   - мантисса,   - основание степени,   - показатель степени.

Такой метод является компромиссом между точностью и диапазоном представляемых значений. Представление чисел с плавающей точкой рассмотрим на примере чисел двойной точности (double precision). Такие числа занимают в памяти два машинных слова (8 байт на 32-битных системах). Наиболее распространенное представление описано в стандарте IEEE 754.Кроме чисел двойной точности также используются следующие форматы чисел:

---

• 
  половинной точности (half precision) (16 бит),
  
• 
  одинарной точности (single precision) (32 бита),
  
• 
  четверной точности (quadruple precision) (128 бит),
  
• 
  расширенной точности (extended precision) (80 бит).
  

При выборе формата программисты идут на разумный компромисс между точностью вычислений и размером числа.[править]Нормальная и нормализованная формы

Определение:

Нормальной называется форма представления числа, при которой абсолютное значение мантиссы десятичного числа находится на полуинтервале  .

Недостатком такой записи является тот факт, что числа нельзя записать однозначно:  .

Определение:

Нормализованной называется форма представления числа, при которой абсолютное значение мантиссы десятичного числа лежит на полуинтервале  , а двоичного на полуинтервале  .

[править]Числа двойной точностиЧисло с плавающей точкой хранится в нормализованной форме и состоит из трех частей (в скобках указано количество бит, отводимых на каждую секцию в формате double):

1. 
   знак
   
2. 
   экспонента (показатель степени) (в виде целого числа в коде со сдвигом)
   
3. 
   мантисса (в нормализованной форме)
   

В качестве базы (основания степени) используется число  . Экспонента хранится со сдвигом  .

Знак
	Экспонента (11 бит)												Мантисса (52+1 бит)
0	0	0	0	0	0	0	0		0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	000
	62				52									51																																																0

---

Утверждение:

Итоговое значение числа вычисляется по формуле:  .

[править]Свойства чисел с плавающей точкой

1. 
   В нормализованном виде любое отличное от нуля число представимо в единственном виде. Недостатком такой записи является тот факт, что невозможно представить число 0.
   
2. 
   Так как старший бит двоичного числа, записанного в нормализованной форме, всегда равен 1, его можно опустить. Это используется в стандарте IEEE 754.
   
3. 
   В отличие от целочисленных стандартов (например, integer), имеющих равномерное распределение на всем множестве значений, числа с плавающей точкой (double, например) имеют квазиравномерное распределение.
   
4. 
   Вследствие свойства 3, числа с плавающей точкой имеют постоянную относительную погрешность (в отличие от целочисленных, которые имеют постоянную абсолютную погрешность).
   
5. 
   Очевидно, не все действительные числа возможно представить в виде числа с плавающей точкой.
   
6. 
   Точно в таком формате представимы только числа, являющиеся суммой некоторых обратных степеней двойки (не ниже -53). Остальные числа попадают в некоторый диапазон и округляются до ближайшей его границы. Таким образом, абсолютная погрешность составляет половину величины младшего бита.
   
7. 
   В формате double представимы числа в диапазоне  .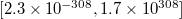
   

[править]Особые значения чисел с плавающей точкой[править]Ноль (со знаком)В нормализованной форме невозможно представить ноль. Для его представления в стандарте зарезервированы специальные значения мантиссы и экспоненты.

Знак
	Экспонента						Мантисса
0/1	0	0	0	0	0		1,	0	0	0	0	0	0	0	0	0	0	=

---

Согласно стандарту выполняются следующие свойства:

• 
  
  
• 
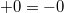
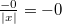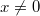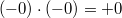
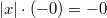
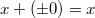
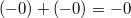
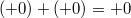
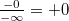
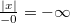   (если  )
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
   (если  )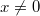
  

[править]Бесконечность (со знаком)Для приближения ответа к правильному при переполнении, в double можно записать бесконечное значение. Так же, как и в случае с нолем, для этого используются специальные значение мантиссы и экспоненты.

Знак
	Экспонента						Мантисса
0/1	1	1	1	1	1		1,	0	0	0	0	0	0	0	0	0	0	=

---

Бесконечное значение можно получить при переполнении или при делении ненулевого числа на ноль.[править]НеопределенностьВ математике встречается понятие неопределенности. В стандарте double предусмотрено псевдочисло, которое арифметическая операция может вернуть даже в случае ошибки.

Знак

Экспонента

Мантисса

0/1

1

1

1

1

1

1,

0/1

0/1

0/1

0/1

0/1

0/1

0/1

0/1

0/1

0/1

=

Неопределенность можно получить в нескольких случаях. Приведем некоторые из них:

• 
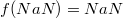  , где 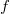  - любая арифметическая операция
  
• 
  
  
• 
  
  
• 
  
  
• 
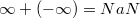
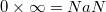
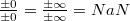
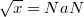  , где 
  

---

Смотрите также файлы

• Курсовая работа по уд "Гражданское право (УД, пм) На тему " Договор комиссии".docx

• Выполнение практических заданий по дисциплине финансовый менеджмент.doc

• Рязанский филиал отчет. О прохождении практики по специальности Юриспруденция в Октябрьском районном отделе судебных приставов г. Рязань уфссп.docx

• ылыми жобаны жазу стандарты.docx

• Составьте таблицу с краткой характеристикой всех психических процессов (ощущение, восприятие, эмоции, сознание, речь, память, воображение и др).docx