[править]Денормализованные числа

Денормализованные (denormalized numbers) - способ увеличить количество представимых числе в окрестности нуля. Каждое такое число по модулю меньше самого маленького нормализованного.< Согласно стандарту числа с плавающей точкой можно представить в следующем виде:

• 
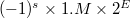  , в нормализованном виде если  ,
  
• 
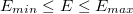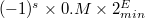  , в денормализованном виде если  ,
  

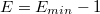где   - минимальное значение порядка, используемое для записи чисел (единичный сдвиг),   - минимальное значение порядка, которое он может принимать - все биты нули, нулевой сдвиг.

Ввиду сложности, денормализованные числа обычно реализуют на программном уровне, а не на аппаратном. Из-за этого резко возрастает время работы с ними. Это недопустимо в областях, где требуется большая скорость вычислений (например, видеокарты). Так как денормализованные числа представляют числа мало отличные от нуля и мало влияют на результат, зачастую они игнорируются (что резко повышает скорость). При этом используются две концепции:

1. 
   Flush To Zero (FTZ) - в качестве результата возвращается нуль, как только становится понятно, что результат будет представляться в денормализованном виде.
   
2. 
   Denormals Are Zero (DAZ) - денормализованные числа, поступающие на вход, рассматриваются как нули.
   

Начиная с версии стандарта IEEE 754 2008 года денормализованные числа называются "субнормальными" (subnormal numbers), то есть числа, меньшие "нормальных".

[править]Машинная эпсилон

Определение:

Машинная эпсилон - наибольшее положительное число  , такое что,  , где   - машинное сложение.

---

Утверждение:

Таким образом, компьютер не различает числа   и  , если  .

Утверждение:

Из свойств чисел двойной точности следует, что для них  .

[править]Unit in the last place (Unit of least precision)

Мера единичной точности используется для оценки точности вычислений.

Определение:

Пусть   - число с плавающей точкой, мантисса которого имеет длину   бит, а экспонента -   бит. Тогда  .

Приведем пример кода на Python, который показывает, при каком значении числа   компьютер не различает числа   и  .

>>> from math import *

>>> x = 1.0

>>> while (x != x + 1):

... x *= 2

...

>>> x

9007199254740992.0

>>> log(x) / log(2)

53.0

То есть  , так как мантисса числа двойной точности содержит 53 бита (в памяти хранятся 52). В C++ для расчета расстояния между двумя числами двойной точности можно воспользоваться функцией 

---

.

[править]Погрешность предиката "левый поворот"

[править]Определения

Утверждение:

Пусть   - множество всех чисел с плавающей точкой с операциями  , , .

Утверждение:

[править]Расчет 

Обозначим  .

Теперь распишем это выражение в дабловой арифметике.





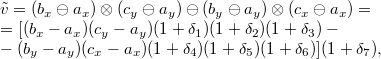
Заметим, что 

Теперь оценим абсолютную погрешность 



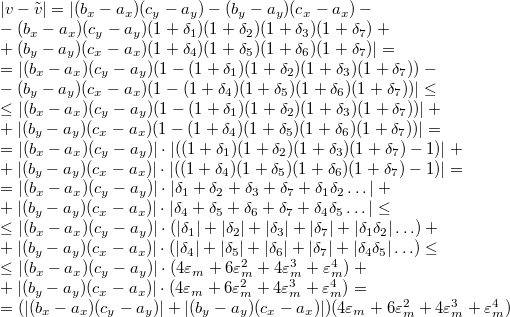
Пусть 

---

 Получаем, что





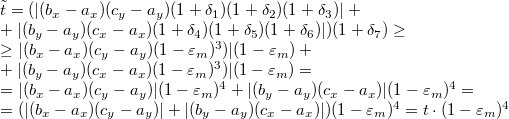
Итого:





[править]Ответ



Заметим, что это довольно грубая оценка. Вполне можно было бы написать   или 

[править]Ссылки

en.wikipedia.org Floating point
en.wikipedia.org Half-precision floating point format
en.wikipedia.org Single precision floating point format
en.wikipedia.org Double precision floating point format
en.wikipedia.org Extended precision floating point format
en.wikipedia.org Quadruple precision floating point format
Goldberg, D. 1991 What every computer scientist should know about floating-point arithmetic
ieee.org IEEE 754
en.wikipedia.org Unit in the last place neerc.ifmo.ru/mediawiki Предикат "левыйповорот"

Категории: 

• 
  В разработке
  
• 
  Вычислительная геометрия
  

• 
  Представиться / зарегистрироваться
  

• 
  Статья
  
• 
  Обсуждение
  

• 
  Чтение
  
• 
  Правка
  
• 
  История
  

Начало формы



Конец формы

Навигация

• 
  Заглавная страница
  
• 
  Сообщество
  
• 
  Текущие события
  
• 
  Свежие правки
  
• 
  Случайная статья
  
• 
  Справка
  

Инструменты

• 
  Ссылки сюда
  
• 
  Связанные правки
  
• 
  Спецстраницы
  
• 
  Версия для печати
  
• 
  Постоянная ссылка
  

• 
  Последнее изменение этой страницы: 11:06, 21 февраля 2012.
  
• 
  К этой странице обращались 41 826 раз.
  

• 
  Политика конфиденциальности
  
• 
  Описание Викиконспекты
  
• 
  Отказ от ответственности
  

• 
  
  

---

---

Смотрите также файлы

• Курсовая работа по уд "Гражданское право (УД, пм) На тему " Договор комиссии".docx

• Выполнение практических заданий по дисциплине финансовый менеджмент.doc

• Рязанский филиал отчет. О прохождении практики по специальности Юриспруденция в Октябрьском районном отделе судебных приставов г. Рязань уфссп.docx

• ылыми жобаны жазу стандарты.docx

• Составьте таблицу с краткой характеристикой всех психических процессов (ощущение, восприятие, эмоции, сознание, речь, память, воображение и др).docx