Файл: Связи и массовых коммуникаций российской федерации федеральное государственное бюджетное образовательное.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 30
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,
СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Кафедра Телевидения и метрологии
Дисциплина: Метрология, стандартизация и сертификация
Контрольная работа
Фамилия: Коломыц
Имя: Денис
Отчество: Александрович
Группа №: РБ-11з
Санкт-Петербург
2023
Оглавление
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ 1
Кафедра Телевидения и метрологии 1
Дисциплина: Метрология, стандартизация и сертификация 1
Фамилия: Коломыц 1
Имя: Денис 1
Отчество: Александрович 1
Группа №: РБ-11з 1
Санкт-Петербург 1
Оглавление 2
Случайная погрешность прибора для измерения сопротивления
изоляции имеет три независимые составляющие, средние квадратические
значения которых равны 0,6 МОм, 0,2 МОм и 1,5 МОм соответственно.
Определите значение результирующей средней квадратической погрешности
прибора и доверительный интервал для однократного измерения
сопротивления изоляции при доверительной вероятности 0,95. Сколько
наблюдений надо сделать, чтобы в три раза уменьшить погрешность измерения
среднего значения сопротивления изоляции? Закон распределения случайной
погрешности прибора принять нормальным.
Случайная погрешность прибора для измерения сопротивления
изоляции имеет три независимые составляющие, средние квадратические
значения которых равны 0,6 МОм, 0,2 МОм и 1,5 МОм соответственно.
Определите значение результирующей средней квадратической погрешности
прибора и доверительный интервал для однократного измерения
сопротивления изоляции при доверительной вероятности 0,95. Сколько
наблюдений надо сделать, чтобы в три раза уменьшить погрешность измерения
среднего значения сопротивления изоляции? Закон распределения случайной
погрешности прибора принять нормальным.
Случайная погрешность прибора для измерения сопротивления
изоляции имеет три независимые составляющие, средние квадратические
значения которых равны 0,6 МОм, 0,2 МОм и 1,5 МОм соответственно.
Определите значение результирующей средней квадратической погрешности
прибора и доверительный интервал для однократного измерения
сопротивления изоляции при доверительной вероятности 0,95. Сколько
наблюдений надо сделать, чтобы в три раза уменьшить погрешность измерения
среднего значения сопротивления изоляции? Закон распределения случайной
погрешности прибора принять нормальным.
Задание 1. ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
Вариант 2
Случайная погрешность прибора для измерения сопротивления изоляции имеет три независимые составляющие, средние квадратические значения
которых равны 0,6 МОм, 0,2 МОм и 1,5 МОм соответственно. Определите
значение результирующей средней квадратической погрешности прибора и
доверительный интервал для однократного измерения сопротивления изоляции при доверительной вероятности 0,95. Сколько наблюдений надо сделать,
чтобы в три раза уменьшить погрешность измерения среднего значения сопротивления изоляции? Закон распределения случайной погрешности прибора принять нормальным.
Решение:
Значение результирующей средней квадратической погрешности
прибора, при условии независимости составляющих, определим по выражению
Значение результирующей средней квадратической погрешности
прибора, при условии независимости составляющих, определим по выражению
Значение результирующей средней квадратической погрешности прибора,
при условии независимости составляющих, определим по выражению
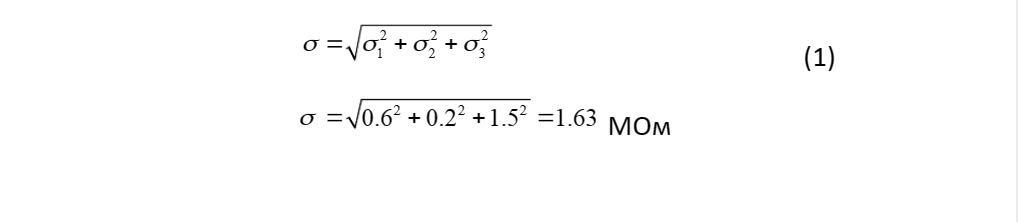
Доверительный интервал Δ определяется функцией распределения
погрешности, доверительной вероятностью и находится из выражения:
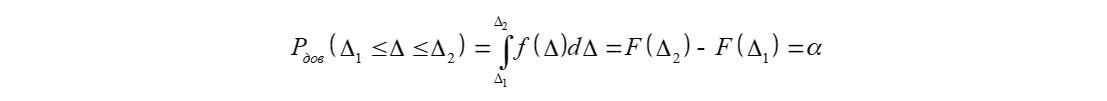
Для нормального закона распределения центральной случайной погрешности доверительный интервал найдем из выражения:
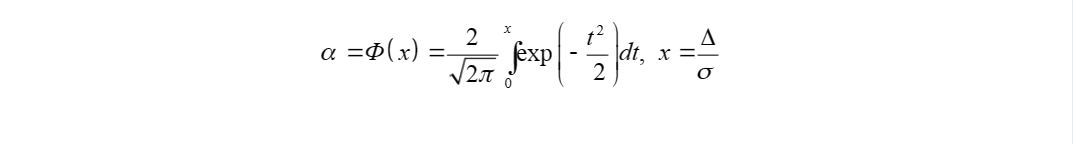
По приложению I (1) для доверительной вероятности =0.95 находим x=1.95
Тогда Δ=1.95×1.63=3.18 МОм.
При усреднении результата измерения по n наблюдениям дисперсия
ее будет связана с дисперсией единичного измерения соотношением
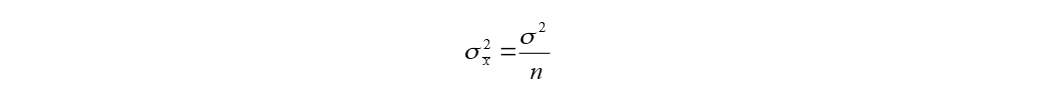
Чтобы в три раза уменьшить погрешность измерения среднего значения сопротивления изоляции, нужно выполнить условие
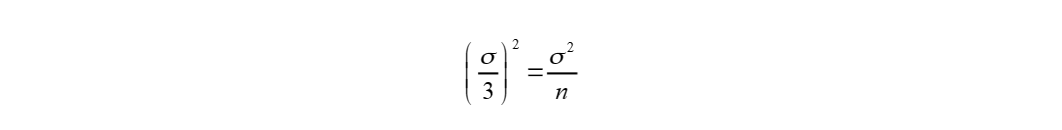
Откуда находим n=9 наблюдений.
Задание 2. ИЗМЕРЕНИЕ ТОКА И НАРЯЖЕНИЯ
Вариант 2
Электронным вольтметром постоянного напряжения, нормируемая
относительная погрешность которого находится в пределах ± 2,0 % , измеряют
сигнал, форма которого показана на рис. 1.
Электронным вольтметром постоянного напряжения, нормируемая относительная погрешность которого находится в пределах ± 2,0 %, измеряют сигнал, форма которого показана на рис. 1.
Вариант 2
Электронным вольтметром постоянного напряжения, нормируемая
относительная погрешность которого находится в пределах ± 2,0 % , измеряют
сигнал, форма которого показана на рис. 1.
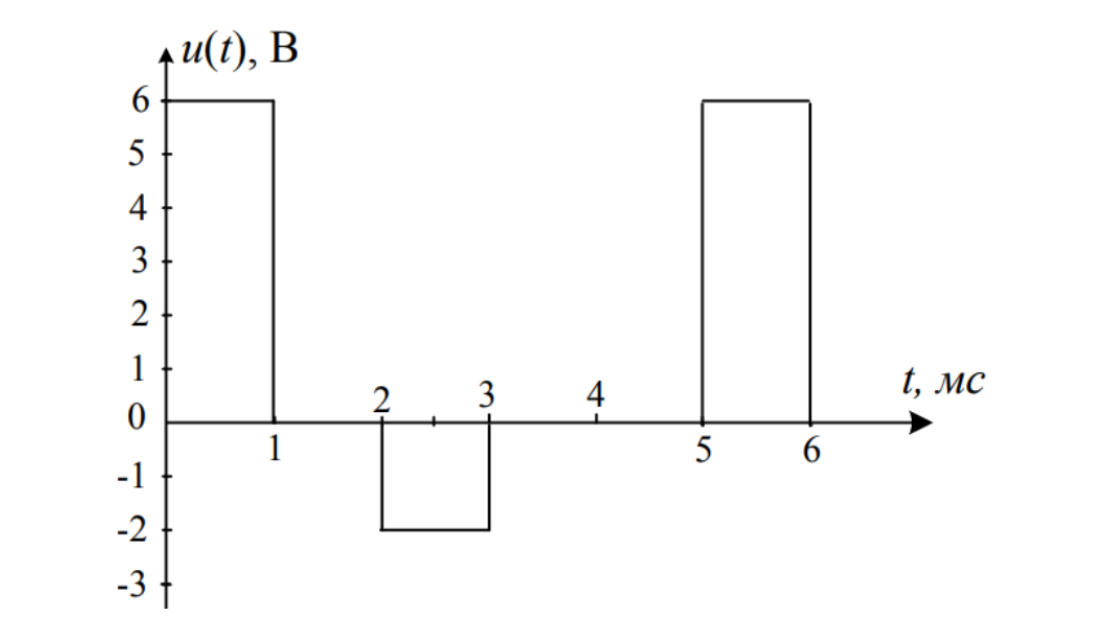
Рисунок 1 – измеряемый сигнал.
Запишите результат измерения постоянной составляющей этого сигнала с оценкой абсолютной погрешности. Изобразите на графике, как изменится этот сигнал при прохождении через RC – цепочку закрытого входа. Определите показания электронного вольтметра переменного напряжения с закрытым входом и выпрямительным преобразователем при измерении такого сигнала. Предел измерения этого вольтметра 2,5 В, а нормируемая относительная погрешность ± 1,5%
Решение:
Вычислим напряжение, на которое откликается вольтметр Uотк – постоянного напряжения
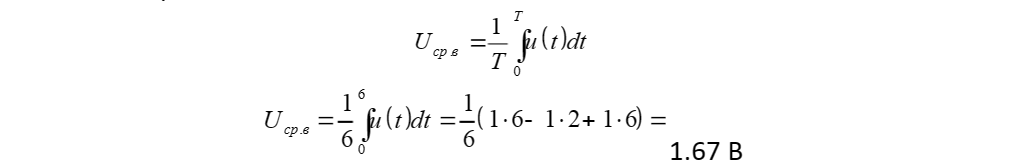
Нормированная относительная погрешность, определяемая выражением
Откуда находим абсолютную погрешность Δ= ±0.02×1.67= ±0.03В
Тогда результат измерения (1.67±0.03) В.
При прохождении через RC цепочку закрытого входа форма входного сигнала его форма изменится (появятся завалы вершин). Форма искажений существенно зависит от времени =R×C; чем больше это время, тем искажения формы входного сигнала будут существенней.
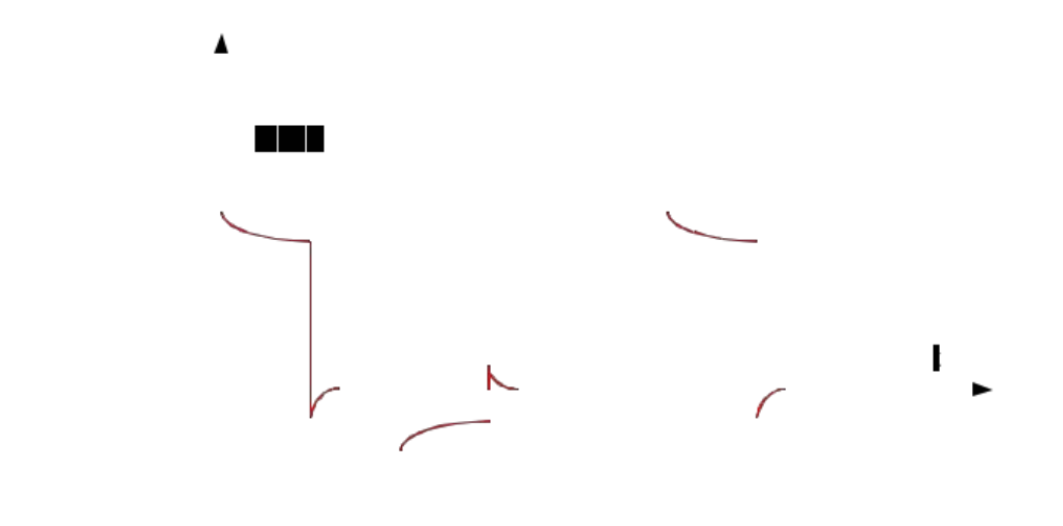
При использовании электронного вольтметра переменного напряжения с
закрытым входом и выпрямительным преобразователем. Принимая во
внимание, что шкала электронного вольтметра градуируется в
среднеквадратическому значению синусоидального тока, т.е. коэффициент
градуировки равен С=1.11
При использовании электронного вольтметра переменного напряжения с
закрытым входом и выпрямительным преобразователем. Принимая во
внимание, что шкала электронного вольтметра градуируется в
среднеквадратическому значению синусоидального тока, т.е. коэффициент
градуировки равен С=1.11
При использовании электронного вольтметра переменного напряжения с закрытым входом и выпрямительным преобразователем. Принимая во внимание, что шкала электронного вольтметра градуируется в среднеквадратическому значению синусоидального тока, т.е. коэффициент градуировки равен С=1.11
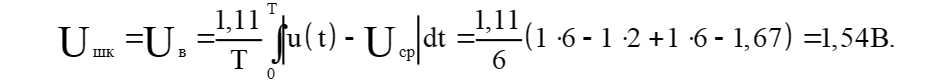
Абсолютную погрешность находим из выражения
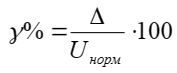- приведенная погрешностьОткуда абсолютная погрешность измерения равна
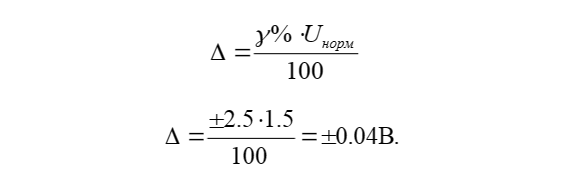
Тогда результат измерения (1.54±0.04) В.
Задание 3. ПРИМЕНЕНИЕ ЭЛЕКТРОННО-ЛУЧЕВОГО
ОСЦИЛЛОГРАФА
Вариант 2
На входы X и Y осциллографа поданы внешние развертывающие
сигналы, форма которых показана на рис. 2. Постройте изображение, которое
получится на экране осциллографа.
На входы X и Y осциллографа поданы внешние развертывающие сигналы, форма которых показана на рис. 2. Постройте изображение, которое получится на экране осциллографа.
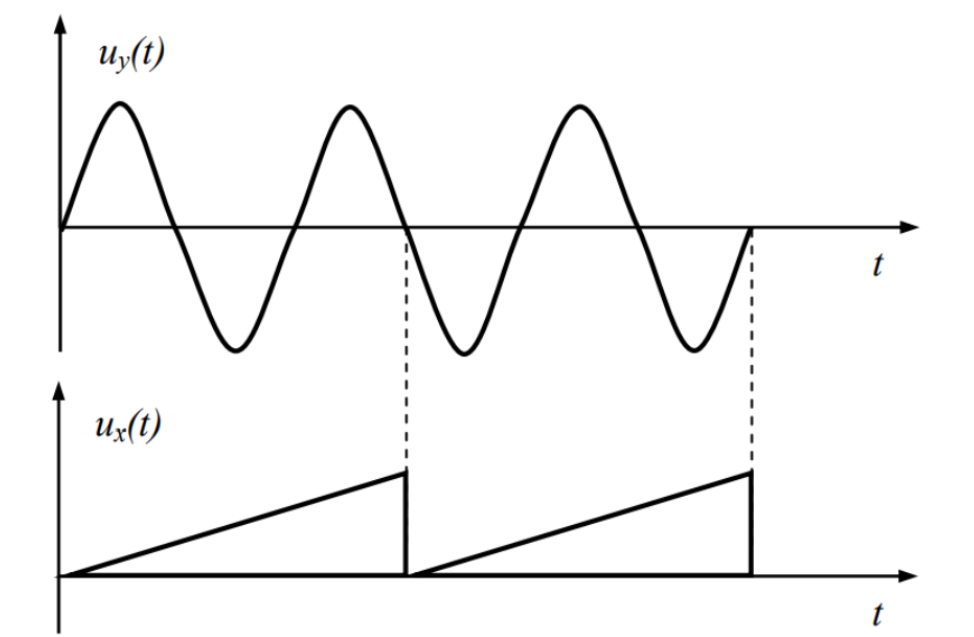
Рисунок 2 – Развертывающие сигналы.
Решение.
Принимая во внимание линейную зависимость между размером отклонения луча на экране и приложенным к пластинам напряжения отклонения, построим изображение, которое получается на экране осциллографа. Из формы развертывающих сигналов видим, что, когда ux(t) изменяется по линейному закону, uy(t) изменяется по гармоническому закону, причем периоды сигналов по х и у совпадают. Осциллограмма показана на рис. 3
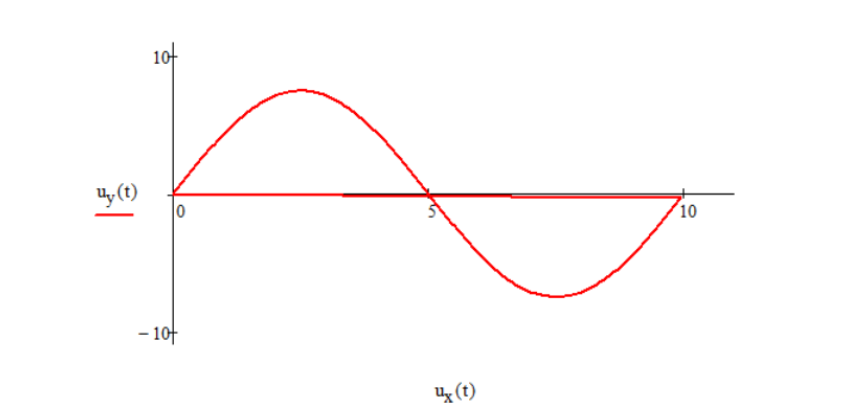
Рисунок 3 – Результирующая осциллограмма.
Задание 4. ЦИФРОВЫЕ ИЗМЕРЕНИЯ ЧАСТОТЫ И
ИНТЕРВАЛОВ ВРЕМЕНИ
Вариант 2
Оцените, с какой абсолютной погрешностью можно измерить период напряжения питающей сети, если отношение сигнал-шум в измеряемом сигнале 40 дБ. В распоряжении имеется цифровой частотомер со следующими характеристиками: относительная погрешность опорного кварцевого генератора находится в пределах ±5·10–6; частота меток времени, формируемых из сигнала опорного генератора, может быть установлена равной0,1; 1 или 10 МГц. Напишите формулу для суммарной абсолютной погрешности измерения периода, назовите составляющие суммарной погрешности, выберите частоту меток времени, оцените абсолютную погрешность измерения периода частоты сети, запишите в соответствии с правилами (см. введение) возможный результат измерения.
Решение:
В режиме измерения периода суммарная абсолютная погрешность
измерений с помощью электронно-счетного частотомера определяется тремя
составляющими:
В режиме измерения периода суммарная абсолютная погрешность измерений с помощью электронно-счетного частотомера определяется тремя составляющими:
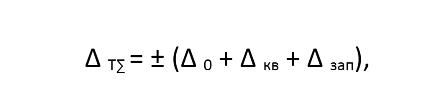
где Δ0 - составляющая абсолютной погрешности, обусловленная погрешностью внутреннего кварцевого генератора:
Δ кв - абсолютная погрешность квантования (дискретности) в режиме измерения периода, определяется выбранным значением периода меток времени Т0 и рассчитывается по формуле:
