Содержание
1. Линейно зависимые и линейно независимые системы векторов…………….2

2. Критерий линейной зависимости системы векторов…………………………2

3. Примеры линейной зависимости системы, состоящей из 1,2,3 векторов……3

Список использованной литературы……………………………………………..5

1. Линейно зависимые и линейно независимые системы векторов
Важными понятиями в теории линейных пространств являются понятия линейной комбинации векторов, линейно зависимой и линейно независимой системы векторов.

Рассмотрим набор из p n-мерных векторов, обозначим их следующим образом. Составим линейную комбинацию этих векторов и произвольных чисел (действительных или комплексных). Отталкиваясь от определения операций над n-мерными векторами, а также свойств операций сложения векторов и умножения вектора на число, можно утверждать, что записанная линейная комбинация представляет собой некоторый n-мерный вектор, то есть.

Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов называется линейно зависимой.

Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.
2. Критерий линейной зависимости системы векторов
Система векторов является линейно зависимой тогда и только тогда, когда хотя бы один из векторов этой системы является линейной комбинацией остальных векторов этой системы.

Для того, чтобы система векторов линейного пространства была линейно зависма, необходимо и достаточно, чтобы хотя бы один из векторов системы линейно выражался через остальные векторы системы (мог быть представлен в виде разложения по векторам системы).

Система векторов ·i, j + k , i − j − k линейного пространства R3 геометрических радиусов векторов трехиерного пространства линейно зависима.

Вектор i − j − k линейно выражается через векторы i и j + k: i − j − k = i − (j + k).

Система векторов, содержащая пару взаимно противоположных векторов, линейно зависима.

Рассмотрим линейно зависимую систему, содержащую пару взаимно противоположных векторов, e1, ..., ek, x, −x.

Вектор −x линейно выражается через остальные векторы системы:

---

−x = 0·e1 +0·e2 + ...+ 0·ek + ( −1)·x.
3. Примеры линейной зависимости системы, состоящей из 1,2,3 векторов
Чтобы проверить является ли система векторов линейно-зависимой, необходимо составить линейную комбинацию этих векторов , и проверить, может ли она быть рана нулю, если хот один коэффициент равен нулю.

Случай 1. Система векторов задана векторами



Составляем линейную комбинацию



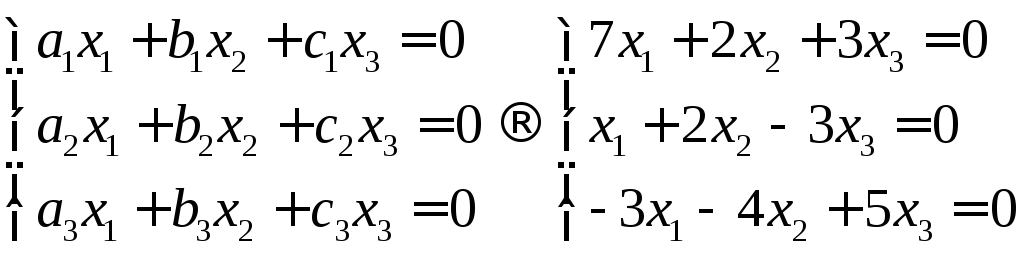
Мы получили однородную систему уравнений. Если она имеет ненулевое решение, то определитель должен быть равен нулю. Составим определитель и найдем его значение.



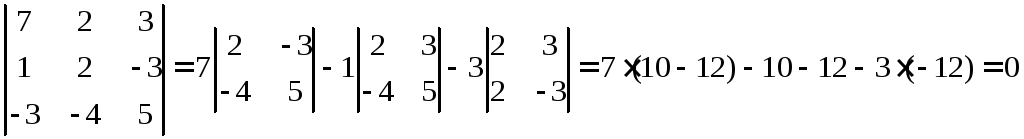
Определитель равен нулю, следовательно, вектора линейно зависимы.

Случай 2. Система векторов заданна аналитическими функциями:

a) , если тождество верно, значит система линейно зависима.

Составим линейную комбинацию.



Необходимо проверить, существуют ли такие a, b, c (хотя бы одна из которых не равна нулю) при которых данное выражение равно нулю.

Запишем гиперболические функции

, , тогда

,

тогда линейная комбинация векторов примет вид:

,

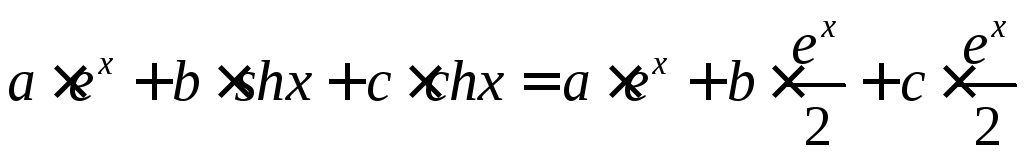откуда , возьмем, например,

---

, тогда линейная комбинация равна нулю, следовательно, система линейно зависима.

Ответ: система линейно зависима.

b) , составим линейную комбинацию



Линейная комбинация векторов, должна быть равна нулю для любых значений x.

Проверим для частных случаев.





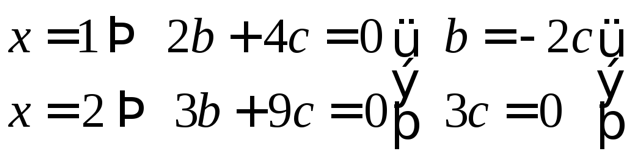
Линейная комбинация векторов равна нулю, только если все коэффициенты равны нулю.

Следовательно, система линейно не зависима.

Ответ: система линейно не зависима.
Список использованной литературы

1. 
   Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский. – М.: Юрайт, 2016. – 281 с
   
2. 
   Линейная алгебра: учеб. пособие / Н.В. Гредасова, М.А. Корешникова, Н.И. Желонкина [и др.]; Мин-во науки и высш. образования РФ. – Екатеринбург: Изд-во Урал. ун-та, 2019. – 88 с.
   
3. 
   Канатников А.Н. Крищенко А.П. Линейная алгебра / А.Н. Канатиков, А.П. Крищенко. – М.: Издательство МГТУ им. Баумана, 2015. – 336 c.
   

---

Смотрите также файлы

• Земля Санникова Другу Игорю А. посвящается.docx

• Компьютерные вирусы. Основные понятия и классификация.docx

• Государственное бюджетное прфессиональное образовательное учреждение московской области балашихинский техникум.docx

• Автор Потапова П. О.docx

• Аттестационный лист Гайдук Ольга Игоревна, (Ф. И. О. обучающегося) обучающий(ая)ся группы окк22009мо по специальности 38. 02. 04 Коммерция (по отраслям).docx