_{Задание № 13}8. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0).



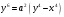
Решение:

Составим уравнение этой кривой в полярных координатах с помощью замены:















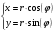
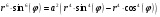
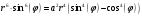
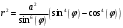
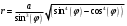
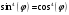
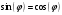
Построим график этой функции:



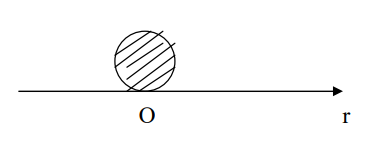
В силу симметрии фигуры:













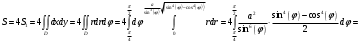
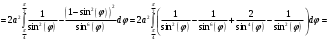
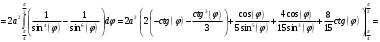
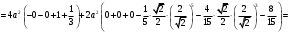
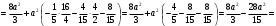
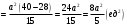
Ответ:

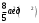
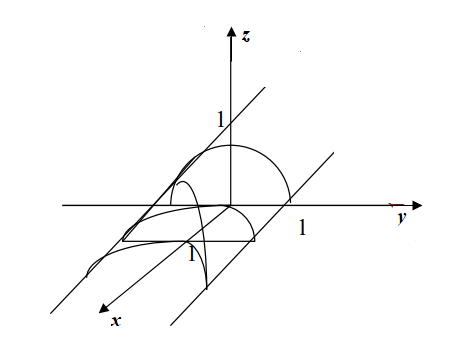
Задание № 148. Вычислить с помощью тройного интеграла объем тела, ограниченного поверхностями. Сделать чертеж данного тела и его проекции на плоскость

z = 0, z = 1 - y², x = y², x = 2y² + 1

Решение:

Сделаем чертеж.

z = 1- y² - параболический цилиндр, ограниченный плоскостями, параллельными оси Oz:

x = y² и x = 2y² + 1 – параболы



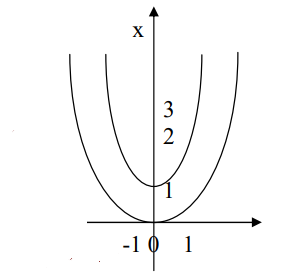
Проекция тела на плоскость

---

Объем тела:





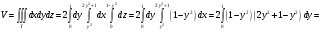
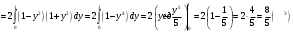
Ответ:

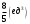
Задание № 158. Вычислить криволинейный интеграл

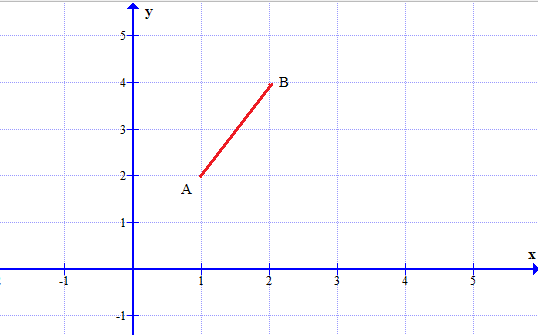
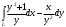вдоль отрезка L = AB прямой от точки А (1; 2) до В (2; 4)

Сделать чертеж.

Решение:

Сделаем чертеж.



Уравнение прямой, проходящей через две точки



,

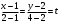
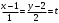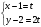
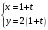y = 2x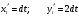



Следовательно: в точке (А) t = 0, в точке (В) t = 1





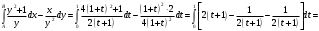
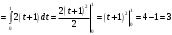
Ответ: 3

Задание № 168. Даны векторное поле 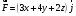и плоскость Р: x+y+2z-4 = 0 , которая совместно с координатными плоскостями образует пирамиду V. Пусть  - основание пирамиды, принадлежащее этой плоскости,  - контур, ограничивающий  , n- нормаль к  , направленная вне пирамиды. Требуется вычислить:

1) Поток векторного поля F через поверхность  в направлении нормали n,

2) Циркуляцию векторного поля F по замкнутому контуру  непосредственно и применив теорему Стокса к контуру  и ограниченной им поверхности  с нормалью n.

3) Поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормаль к её поверхности непосредственно и применив теорему Остроградского.

Сделать чертеж.

Решение:



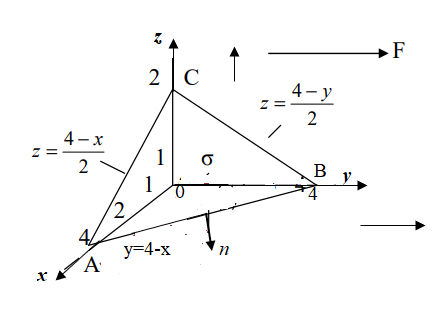
Векторная функция F направлена вдоль оси у

1) Поток П векторного поля F через поверхность σ равен поверхностному интегралу



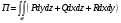
Подставляем

---

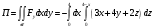
Поскольку вектор нормали 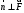, то поток равен нулю: П = 0

2) Циркуляция Ц векторного поля F по контуру λ равна линейному интегралу

Непосредственное вычисление



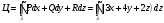
Контур  состоит из 3-х отрезков: ОА, АВ и ВО:



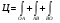
1) Отрезок ОА: z = 0; y = 0



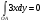
2) Отрезок АB: z = 0



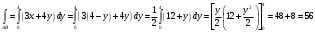
2) Отрезок BO





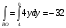
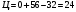
Найдем циркуляцию по формуле Стокса

Согласно теореме Стокса:



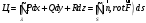
Вычисляем :





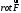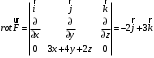
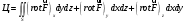
Поток через поверхность σ:

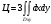, где Dxy – область интегрирования, проекция поверхности S на плоскость ху системы координат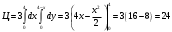



3) Поток векторного поля F через полную поверхность пирамиды V

Теорема Остроградского – Гаусса



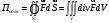
Находим







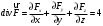
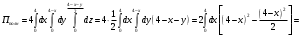
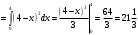
Непосредственное вычисление



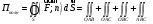
Поток через грани OBС и ОAВ равен нулю, поскольку вектора нормали граней перпендикулярны







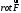
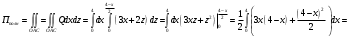
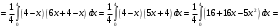
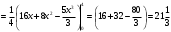
Ответ: П = 0, Ц = 24,

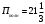
Задание № 178. Проверить, является ли векторное поле F=Xi+Yj+Zk потенциальным и соленоидальным.

---

В случае потенциальности поля F найти его потенциал.



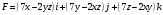
Решение:

Для потенциальности поля необходимо и достаточно, чтобы









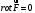
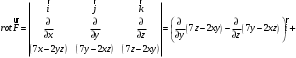
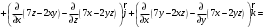
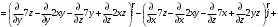
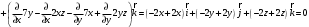
Поле F потенциально.

Для соленоидальности поля:



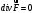
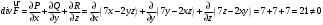
Таким образом, поле не является соленоидальным.

Потенциал можно вычислить по формуле:



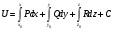
Выберем в качестве точки (x₀, y₀, z₀) точку (0, 0, 0)



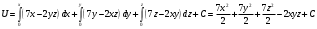
Задание № 188. Найти общее решение дифференциального уравнения



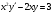
Решение:

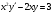/x⁴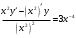



Используем правило дифференцирования 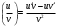получаем

=>

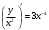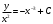
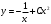- общее решение уравнения

Ответ:

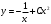
Задание № 198. Найти общее решение дифференциального уравнения



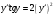
Решение:



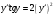
Пусть

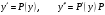
Уравнение примет вид:



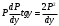
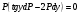P = 0 => y’ = 0 => y = C

=>

---

=>

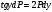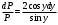
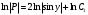
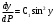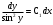
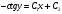- общее решение уравнения C₁ = -C₁; C₂ = -C₂

Ответ:

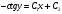
Задание № 208. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.

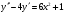y(0) = 2,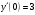

Решение:

Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.

Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r² – 4r = 0, r(r – 4) = 0

Корни характеристического уравнения:

r₁ = 4

r₂ = 0

Следовательно, фундаментальную систему решений составляют функции:



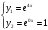
Общее решение однородного уравнения имеет вид:



Рассмотрим правую часть:



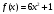
Поиск частного решения.

Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:

R(x) = e^αx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) - некоторые полиномы

имеет частное решение

y(x) = x^ke^αx(R(x)cos(βx) + S(x)sin(βx))

где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).

Здесь P(x) = 6x² + 1, Q(x) = 0, α = 0, β = 0.

Следовательно, число α + βi = 0 является корнем характеристического уравнения.

Уравнение имеет частное решение вида:

y^· = x (Ax² + Bx + C)

Вычисляем производные:

y' = A·x²+B·x+C+x(2·A·x+B)

y'' = 2(3·A·x+B)

которые подставляем в исходное дифференциальное уравнение:

y'' -4y' = (2(3·A·x+B)) -4(A·x²+B·x+C+x(2·A·x+B)) = 6·x²+1

или

-12·A·x²+6·A·x-8·B·x+2·B-4·C = 6x²+1

Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:

---

Смотрите также файлы

• Правой режим использования и охраны лесов.ppt

• 1. Завещание Ярослава Мудрого. Правление Ярославичей Любечский съезд 1097 г.docx

• Методические рекомендации для обучающихся по составлению и выполнению отчета о прохождении всех видов практики специальность 40. 02. 01. Право и организация социального обеспечения.doc

• Протокол 1 Утверждена приказом директора мбоу Ягульская сош от 29. 08. 2022 г. 1535 Директор школы.docx

• Домашнее задание Задание 1 Имеются следующие данные.docx