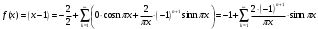Файл: Решение Составим уравнение этой кривой в полярных координатах с помощью замены.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
x2: -12A = 6
x: 6A – 8B = 0
1: 2B – 4C = 1
Решая ее, находим:
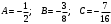
Частное решение имеет вид:
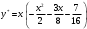
Таким образом, общее решение дифференциального уравнения имеет вид:
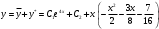
Найдем частное решение при условии: y(0) = 2, y'(0) = 3
Поскольку y(0) = С1+С2, то получаем первое уравнение:
С1+С2 = 2
Находим первую производную:
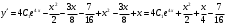
Поскольку y'(0) = 4*С1 – 7/16, то получаем второе уравнение:
4*С1 – 7/16 = 3
В итоге получаем систему из двух уравнений:
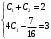
которую решаем методом исключения переменных.
С1 = 55/64, С2 = 73/64
Тогда частное решение при заданных начальных условиях можно записать в виде:
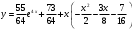
Ответ: общее решение дифференциального уравнения -
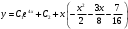
частное решение -
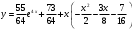
Задание № 218. Исследовать сходимость числового ряда
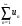
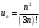
Решение:
Воспользуемся признаком Даламбера.
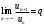
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).
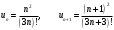
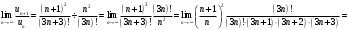
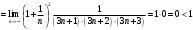
Поскольку q < 1, то ряд сходится.
Задание № 228. Найти интервал сходимости степенного ряда
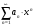
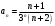
Решение:
Определяем радиус сходимости
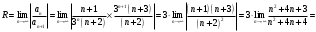
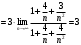
Интервал сходимости данного ряда определяется неравенством
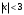
или
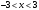
Исследуем сходимость ряда на концах этого интервала
При
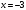получаем ряд: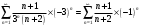
Исследуем сходимость ряда при помощи признаков сходимости.
Рассмотрим первые три члена ряда:
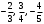
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
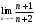
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется
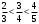
б) По второму признаку Лейбница предел ряда должен стремится к 0.
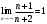
Второе условие Лейбница не выполняется.
Таким образом, рассматриваемый ряд расходится (один из признаков не выполняется).
Ряд расходится, значит, x = -3 - точка расходимости.
При
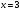получаем ряд: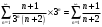
Исследуем его сходимость при помощи признаков сходимости.
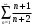
Исходное выражение можно упростить
, 
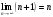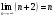
Тогда исходный ряд можно представить в виде:
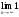
Исследуем сходимость ряда при помощи интегрального признака сходимости Коши.
Рассмотрим несобственный интеграл:
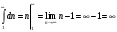
Так как несобственный интеграл расходится, то расходится и исследуемый ряд.
Значит, x = 3 - точка расходимости.
Таким образом, данный степенной ряд является сходящимся при:
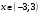
Задание № 238. Разложить функцию
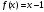в ряд Фурье в интервале (-1; 1)
Решение:
Для разложения функции с периодом 2l в ряд Фурье и вычисление его коэффициентов используем формулы:
; 
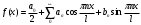
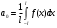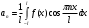
; где n = 0, 1, 2….
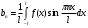; где n = 0, 1, 2….В нашем случае l = 1, а точка x =0 разбивает интервал (-1; 1) на две части
Вычислим a0:
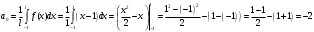
Вычисляем an:
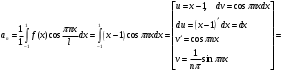
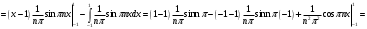
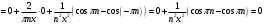
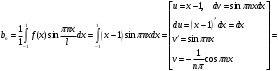
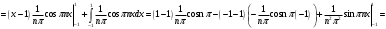
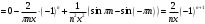
Подставим эти коэффициенты в разложение ряда:
