Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Саратовский государственный технический университет имени Гагарина Ю.А.»

Контрольная работа
по дисциплине «Техническая механика»
направления подготовки 15.03.01 «Машиностроение» (бакалавр)

Выполнил: студент

МНСТ

курс 1

специальность б-МНСТипу-11

форма обучения заочная

шифр 201558

Ф.И.О. Корешков Сергей Александрович

Проверил:

Доктор технических наук, профессор

Артамонова Елена Николаевна
Дата 11.06.22

Саратов - 2022

Содержание

1. 
   Введение 3-4
   
2. 
   Растяжение, сжатие стержня 5
   
3. 
   Кручение, сдвиг, смятие стержня 6
   
4. 
   Поперечный изгиб 7-10
   
5. 
   Список использованной литературы 11
   

Введение

Достижения технической механики позволяют не только улучшать кон­струкции машин и механизмов, но и совершенствовать производственные процессы. Сегодня на многих предприятиях широко используются маши­ны-автоматы, автоматические поточные линии, которые без прямого учас­тия человека обеспечивают выпуск готовой продукции, начиная с обработ­ки сырья и заканчивая упаковкой готовых изделий.

Область применения законов механики для решения конкретных техни­ческих задач очень обширна. Наша эпоха научно-технического прогресса с особенной силой подтверждает необозримость практического приложения этой науки.

Техническая механика — это наука об общих законах меха­нического движения и применения их в современной технике.

Техническая механика состоит из двух частей:

• 
  теоретичес­кой
  
• 
  прикладной.
  

Первая часть посвящена изучению теоретических основ механического движения, вторая — использованию положений теоретиче­ской механики для практических целей: проектирования механизмов, рас­чета деталей машин, строительных конструкций и сооружений.

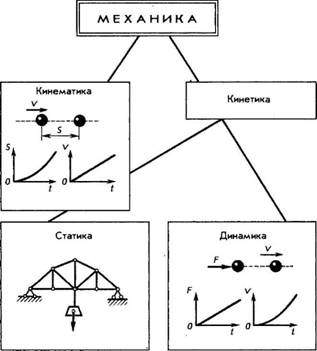
Теоретическую механику принято подразделять на три тесно связанных раздела:

• 
  статику,
  
• 
  кинематику
  
• 
  динамику (рис. 1).
  

В за­дачи теоретической механики входит определение условий, при которых соблюдаются условия равновесия тел. Этот раздел механики называют

---

статикой. Изучением движения тел на основании законов геометрии занимается раздел механики, называемый кинематикой. Раздел ме­ханики, в котором изучается движение тел и рассматриваются причины, его вызвавшие, называют динамикой. Статика, кинематика и динами­ка охватывают все вопросы, связанные с механическим движением тел, и позволяют решать многочисленные практические задачи.

 Р ис. 1

Понятие «тело» является обобщающим. В механике под телом принято понимать все предметы окружающего нас мира: строения, оборудование це­хов, заводов, лабораторий и т. д. Твердое тело — физическое тело, характеризующееся стабильностью формы. Механическим движением тела называется изменение его положения по отношению к другим телам с течением времени.

Прикладная механика также состоит из трех крупных разделов:

• 
  тео­рии механизмов и машин, на основании законов теоретической механики рассматриваются принципы анализа и проектирования механиз­мов
  
• 
  сопротивления материалов, позволяет установить условия прочнос­ти и устойчивости проектируемых конструкций и сооружений
  
• 
  сопротивления деталей машин. посвящены изучению принципов расчета и конструирования деталей и сборочных единиц машин общего назначения.
  

Последовательное изучение всех этих разделов и является предметом технической механики.¹

Растяжение, сжатие стержня
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается, когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.

---

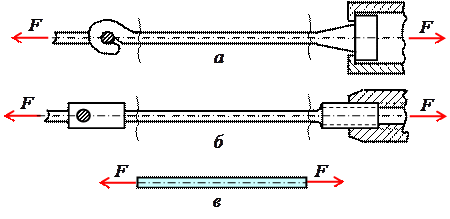
Рис. 1. Растяжение стержня

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z  направлена от сечения (рис. 2, б), а при сжатии – к сечению.²


Рис.2 Нормальная сила N


Кручение, сдвиг, смятие стержня.
С 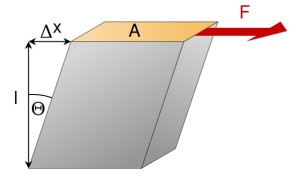двиг – деформация, характеризующаяся взаимным смещением параллельных слоёв материала под действием сил, приложенных касательно к его поверхности, при неизменном расстоянии между слоями (рисунок 1).

Рисунок 1 — Сдвиг

К 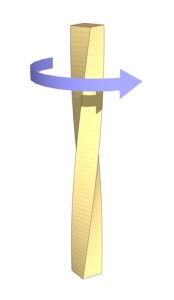ручение – деформация, характеризующаяся взаимным поворотом поперечных сечений тела под действием пары сил (момента) в этих сечениях (рисунок 2).

Рисунок 2 — Кручение

Смятием называют деформацию, представляющую собой нарушение первоначальной формы поверхности под действием силы перпендикулярной к этой поверхности.³

Поперечный изгиб.

Изгибомназывается вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.1). Брус, работающий при изгибе, называется балкой.

Изгиб называетсяплоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.1).



Рис.1. Прямой изгиб

При плоском поперечном изгибе

---

 в балке возникают два вида внутренних усилий: поперечная сила Q_y , где y – ось симметрии (главная центральная ось) и изгибающий момент M_x. , где x – другая главная центральная ось сечения, нормальная к оси симметрии.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.2). При наличии поперечной силы Q_y изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; попереч­ный изгиб относят к простым видам сопротивления условно, так как в большинстве слу­чаев (для достаточно длинных балок) действием поперечной силы при расчетах на проч­ность можно пренебречь.

Косой изгиб- изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.

Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.

Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.

Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.

Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. ⁴

За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.

Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.

Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется 

---

статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 3 показаны эти закрепления. Для неподвижной (рис 3,б) и подвижной (рис. 3,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 3,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.3,в).



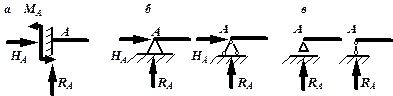
Рис.3. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;

в – в шарнирно-подвижной опоре.

После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).⁵


Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.



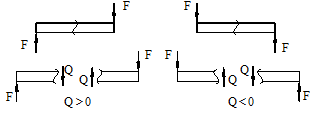
а) б)

Рис.4. а - правило знаков для поперечной силы Q; б - правило знаков для изгибающего момента M.

Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.

---

Смотрите также файлы

• .docx

• Оператор информационных систем и ресурсов.docx

• Решение Замена, тогда, где некоторая функция от.docx

• Тема органы исполнительной власти составьте схему структуры органов исполнительной власти Свердловской области. Вывод.docx

• Афганистан болит в моей душе.docx