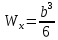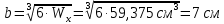ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 148
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
32 вариант
Задание 1.1
Определить реакции стержней, удерживающих груз F в системе - рис. 4. Исходные данные приведены в табл. 1.1.
Дано: схема 3; F=0.6кН
Решение:
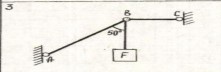
1) Выбираем тело равновесия. Линии действия сил совпадают с линиями действия реакций FAB, FCB стержней АВ и СВ. Линия действия силы F направлена вдоль нити подвеса. Отсюда ясно, что линии действия всех сил приложены к точке В. За тело равновесия принимаем точку (шарнир) В.
2) Строим векторную схему сил, рисунок 1.
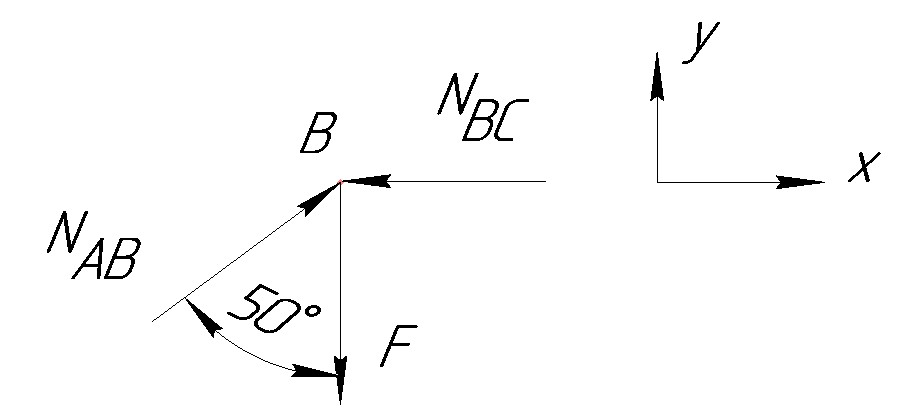
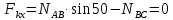
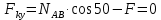
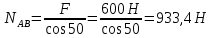
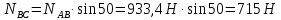
3) Для проверки правильности решения применяем графический метод, в выбранном масштабе М 10Н : 1мм, строим замкнутый силовой треугольник:
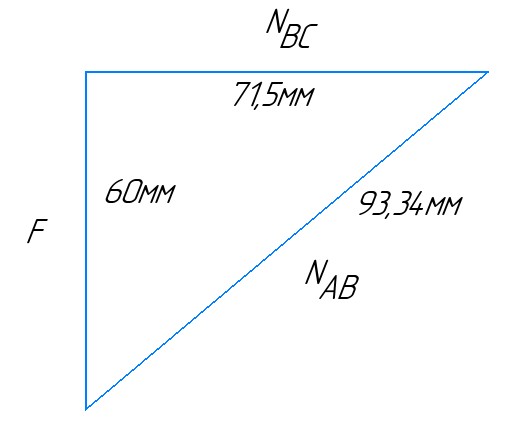
Задание 1.2
Определить реакции опор двухопорной балки. Данные для своего варианта взять из табл. 1.2 и рис. 9.
Дано: схема 10; q=18 Н/м; F=10Н; M=15 Нм
Решение:
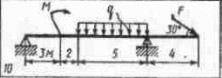
Рисунок 3
1. Изобразим балку с действующими на нее нагрузками (рис. 3).
2. Изображаем оси координат X и Y.
3. Силу F заменяем ее составляющими
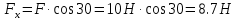
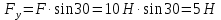
Нагрузка q = 18 Н/м называется силой распределенной (по 18Н на каждый из пяти метров). Ее заменяем вектором Fq = 18 • 5 =90Н, приложенным в середине пяти метров.
4. Освобождаем балку от опор, заменив их опорными реакциями (рис. 4)
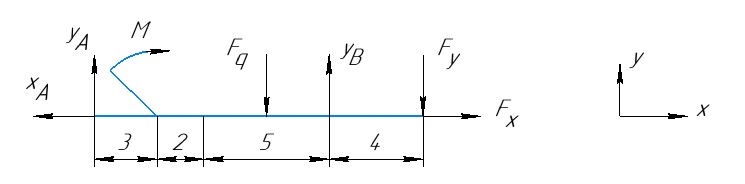
5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор балок используя формулы уравнения равновесия:
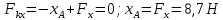
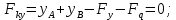
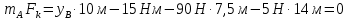
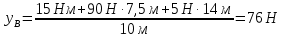
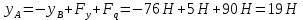
Проверка:
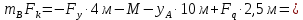
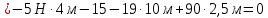
Проверка сходится.
Задание 1.3
Определить недостающие из перечисленных параметры маневра автомобиля: путь S, время t, скорости V1, и V2, ускорение а, движущую силу F, силу инерции Fин, силы трения Ff FK, нормальную реакцию Fn, мощность на передвижение Рn, полную (эффективную) мощность Р
Дано: разгон; V1=0; V2=25 м/с; f=0,5; η=0,91; m=2000кг;
Найти: S; F; Fин; a; Fин; Ff; FK; Рn; Р.
Решение:
1. Объектом приложения сил является автомобиль, размерами которого можно пренебречь, то есть представить его материальной точкой
2. Векторная схема сил включает векторы сил: движущей силы F, силы инерции Fин, трения качения FK, тяжести FT, нормальной реакции FH, рис. 5
3. Уравнения кинетостатики:
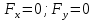
Составляем уравнения для рис. 10
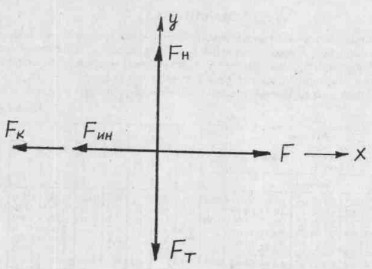
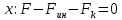
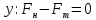
Сила инерции:
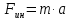
Из формулы ускорения:
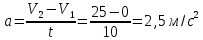
Сила инерции:
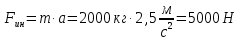
Сила сопротивления качению
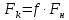
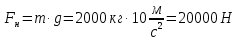
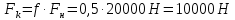
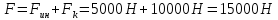
Путь, пройденный автомобилем при разгоне
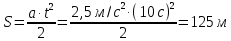
Мощность на передвижение
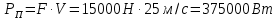
Мощность полная
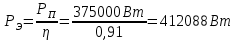
Задание 1.4
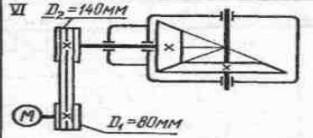
Определить угловые скорости, вращающие моменты, мощности на валах, передаточные отношения, кпд привода. Описать назначение, принцип работы, устройство привода.
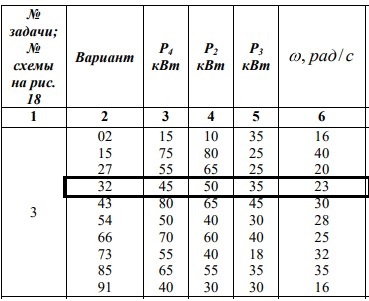
Дано: 6 схема; P1=2,6 Вт; n1=980 об/мин; uр=2,5.
Решение:
1. Определяем передаточное отношение ременной передачи
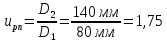
Общее передаточное отношение привода
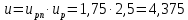
2. Угловые скорости валов привода
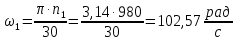
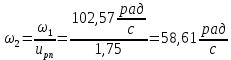
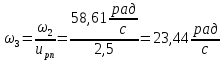
3. частота вращения на валах привода
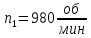
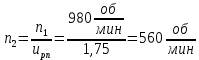
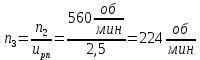
4. Общий коэффициент полезного действия привода
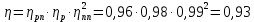
5. Мощности на валах привода
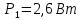
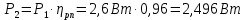
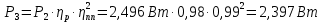
6. Моменты на валах привода
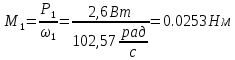
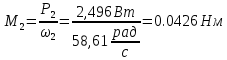
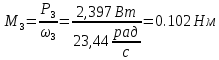
7. Назначение, принцип работы, устройство привода. Привод предназначен для передачи и усилия от электродвигателя к ведомому валу редуктора, изменения направления вращения, изменения частоты вращения в 4,375 раза. Потери мощности составляют 0,203 Вт. Привод устроен из электродвигателя (М), ременной и конической зубчатой передач.
Задание 2.1
Проверить прочность, найти наиболее напряженный участок двухступенчатого бруса, нагруженного силами F1, F2, если [σ] = 160 Н/мм
2. Найти удлинение бруса. Данные своего варианта взять из таблицы 2.1.
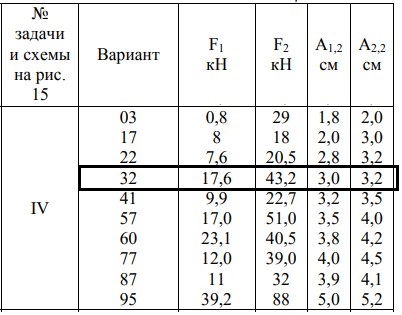
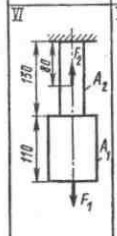
| Решение: | |||
| 1) Определим реакцию опоры R: | |||
| Находим сумму всех сил на ось x: | |||
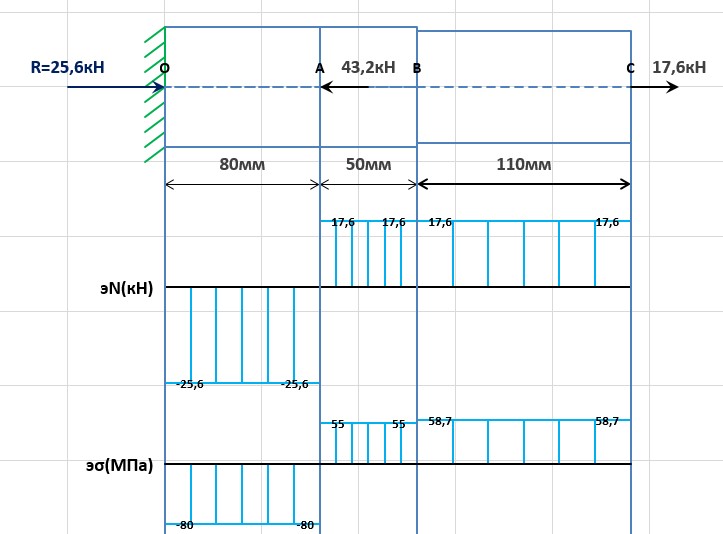
| Fkx=R-43,2кН+17,6кН=0 | |||
| Из этого уравнения, выражаем реакцию R: | |||
| R=-(-43,2кН+17,6кН)=25,6кН | |||
| 3) Находим напряжения на каждом участке: | |||
| σᵢ=Nᵢ/Aᵢ | |||
| σ₁=N₁/A₂=(-25,6кН)/(3,2см²)=-80 МПа; | |||
| σ₂=N₂/A₂=(17,6кН)/(3,2см²)=55МПа; | |||
| σ₃=N₃/A₁=(17,6кН)/(3см²)=58,7МПа; | |||
| Запишем условие прочности: | |||
| maxσ=80МПа≤[σ]=160МПа Все участки выдерживают нагрузку. | |||
| 4) Определяем наибольшие продольные перемещения: | | | |
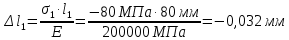
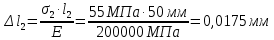
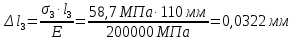
Общее удлинение бруса
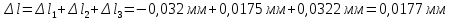
Задание 2.2
Определить диаметр стального вала постоянного сечения из условия прочности, приняв [τ]=30Н/мм2
Исходные данные – в таблице 2.2
Решение
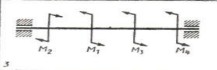
1. Разбиваем вал на три участка - по сечениям, в которых приложены вращающие моменты.
2. Находим вращающие моменты
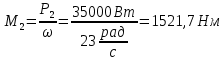
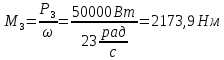
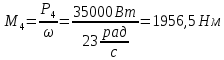
Равномерное вращение обеспечивается условием
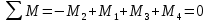
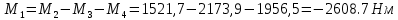
На 1 участке действует момент:
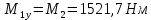
На 2 участке действует момент:
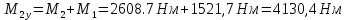
На 3 участке действует момент:
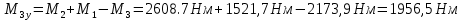
Максимальная нагрузка:
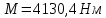
Определяем диаметр вала для наиболее напряженного - второго участка
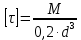
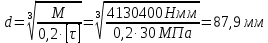
Задание 2.3.
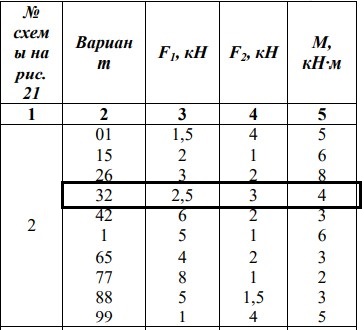
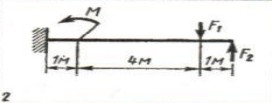
Для стальной балки, нагруженной (рис. 21), построить эпюру изгибающих моментов и подобрать сечение балки в двух вариантах: двутавр и квадрат. Сравнить массы балок по двум расчетным вариантам. Для материала балки принять [σ] = 160 Н/мм2. Данные своего варианта взять из таблицы 2.3.
Решение:
Разбиваем балку на три участка по местам действий силовых факторов: F1, M1, F2
Строим эпюры поперечных сил и изгибающих моментов:
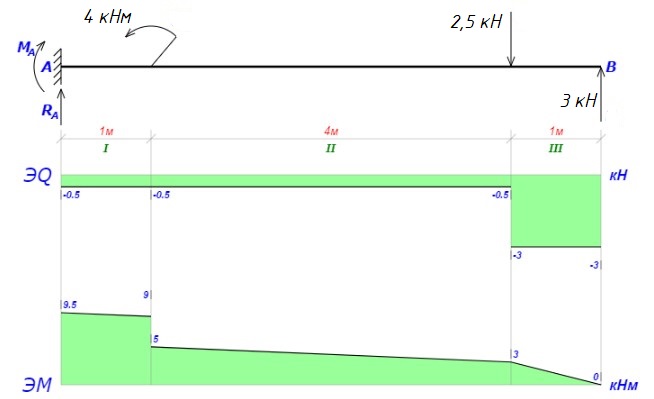
Определяем момент сопротивления сечения в точке заделки: здесь изгибающий момент имеет максимум: Ми = 9,5 кНм
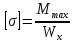
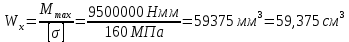
По таблицам сортамента ГОСТ 8239-79 выбираем двутавр 14:
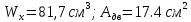
Определим размеры квадрата: