Файл: Задача Исследовать сходимость числового ряда а. К данному знакоположительному ряду применим признак Даламбера.doc
Добавлен: 07.11.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,
0, 1, 2, …
Полученный ряд оказался знакочередующимся. Поэтому используем то же самое условие обеспечения заданной точности, что и в предыдущей задаче:
. (а)
Здесь
,
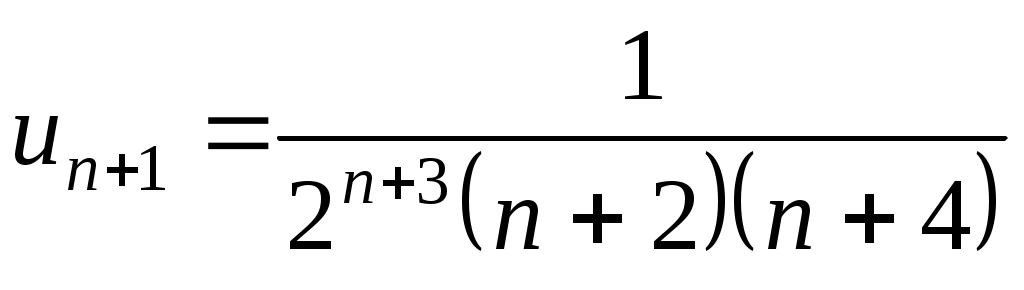поэтому минимально необходимое
находим из условия
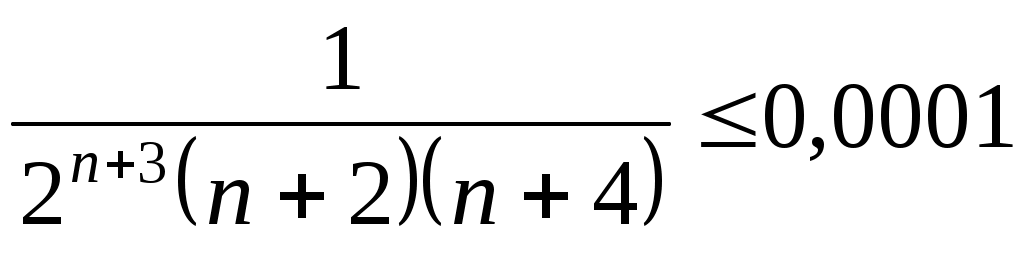, или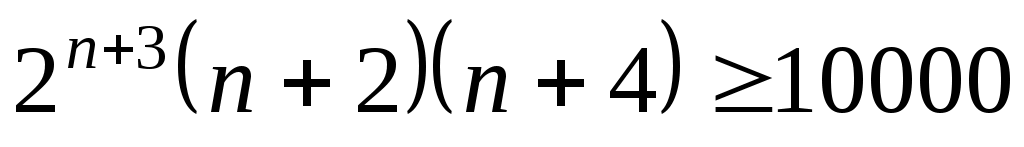 
:
,
.
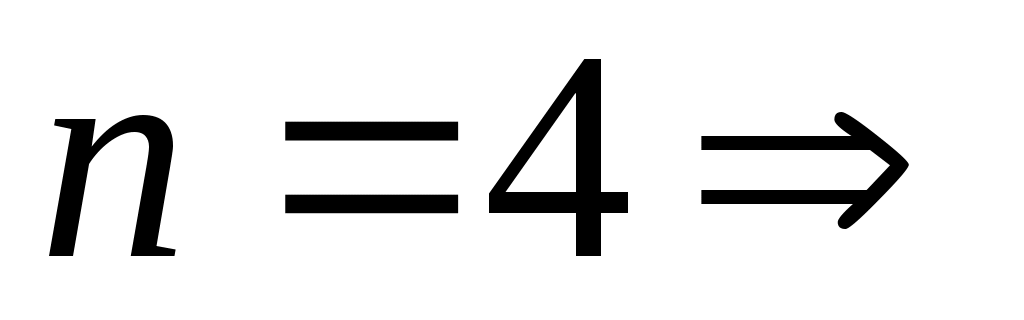
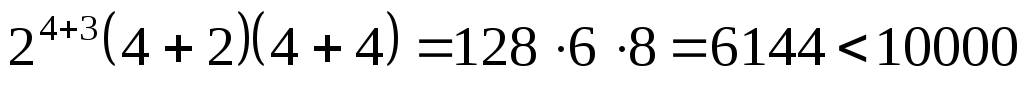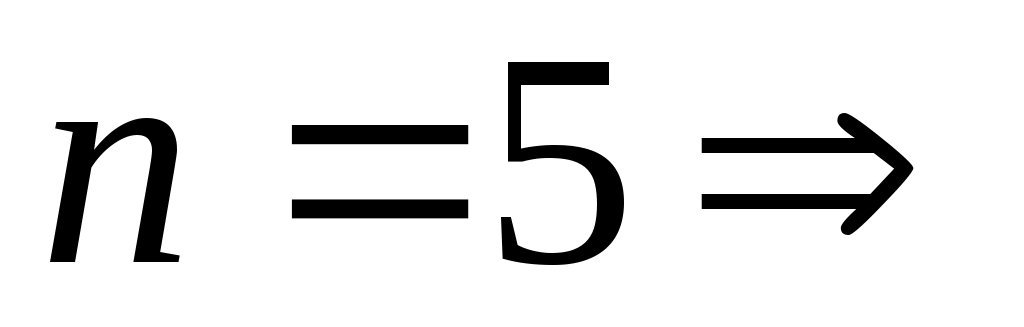
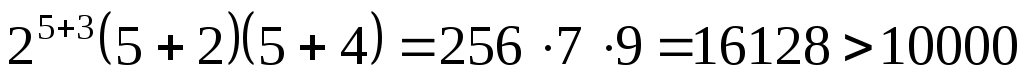Из последнего вытекает, что для обеспечения заданной точности достаточно просуммировать первые шесть членов ряда:
.
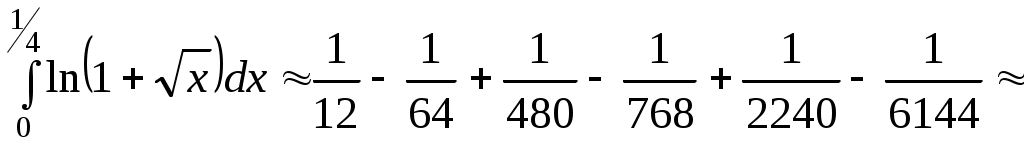
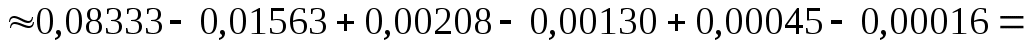
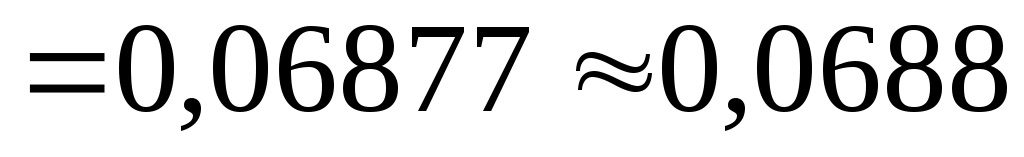Ответ: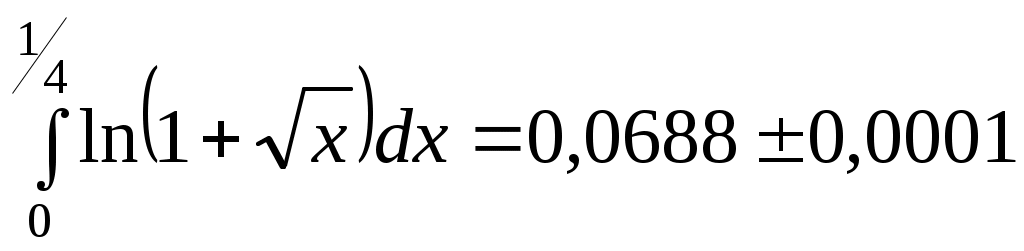
.
Задача 6. Данную функцию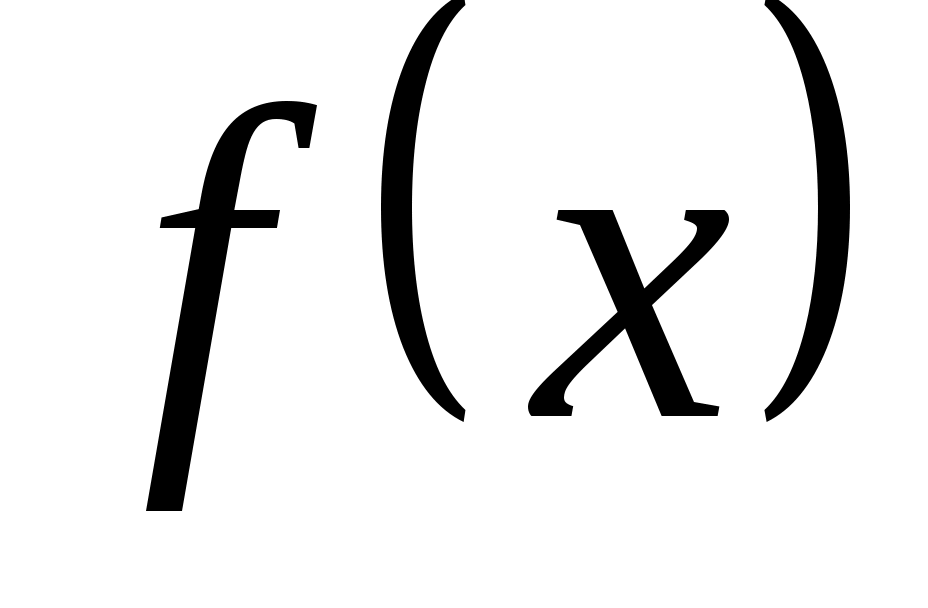
разложить в ряд Фурье в
заданном интервале.
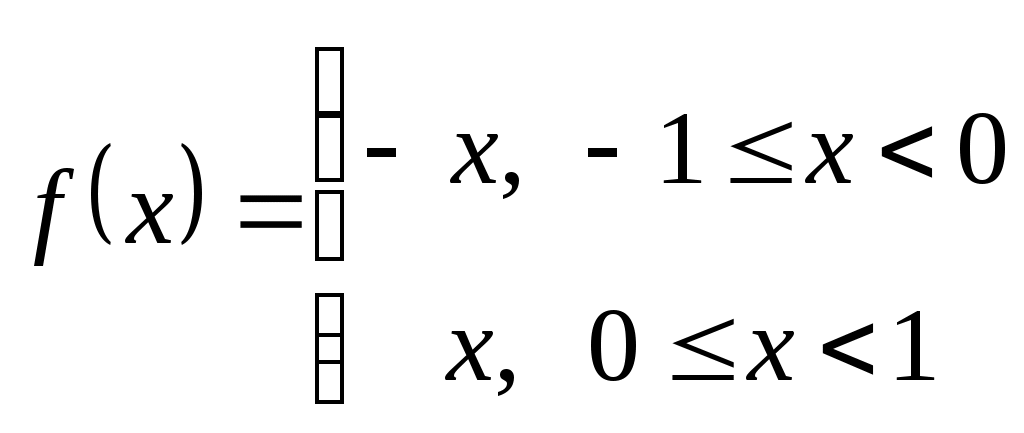, (-1, 1).
Легко убедиться, что в заданном интервале функция непрерывна и, следовательно, может быть представлена своим рядом Фурье в смысле теоремы Дирихле. Кроме того, в рассматриваемом интервале она четная, поэтому ее ряд Фурье должен содержать только четные тригонометрические функции, т.е. косинусы. На этих основаниях записываем:
, 
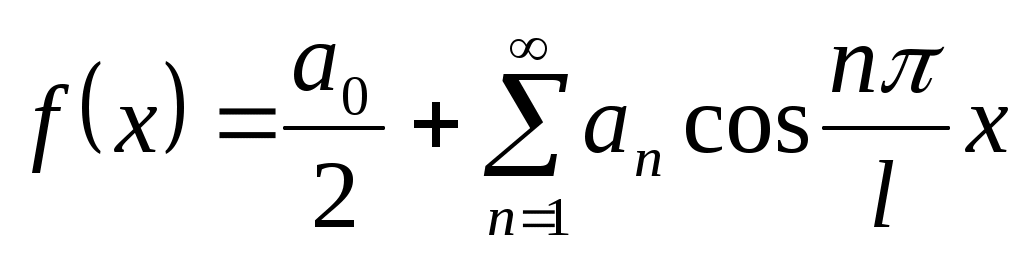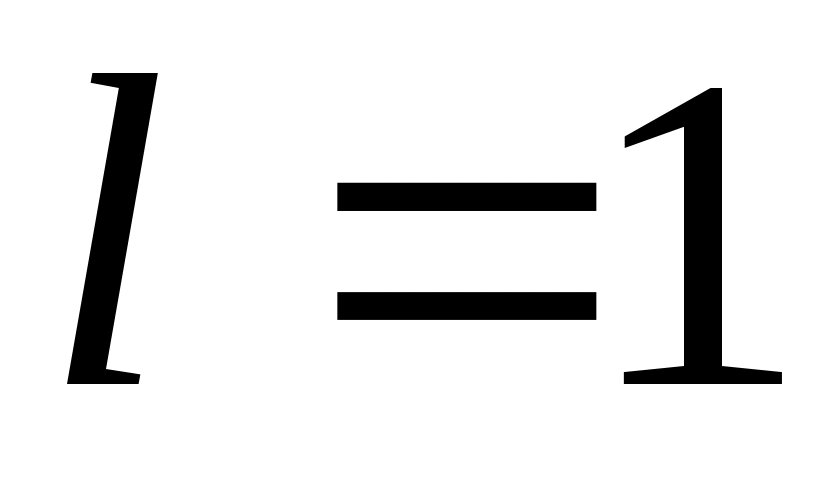. (а)
Находим коэффициенты.
.
.
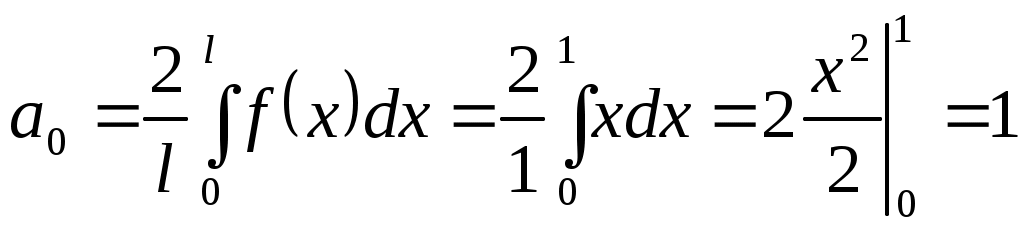
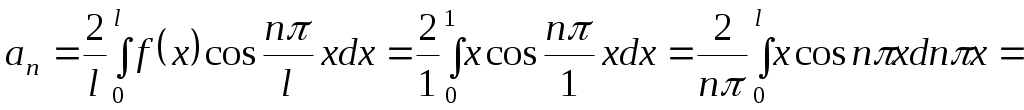
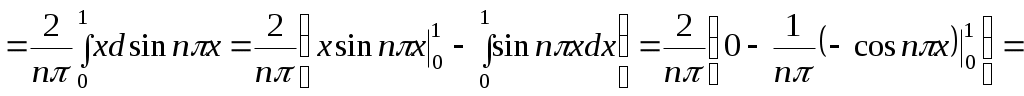
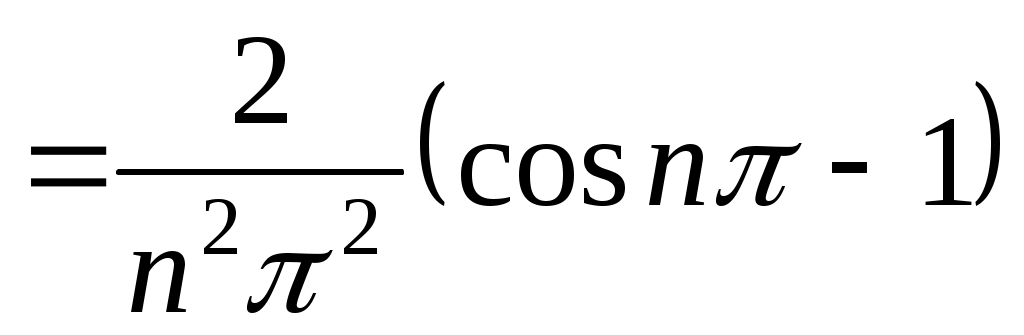Т.к.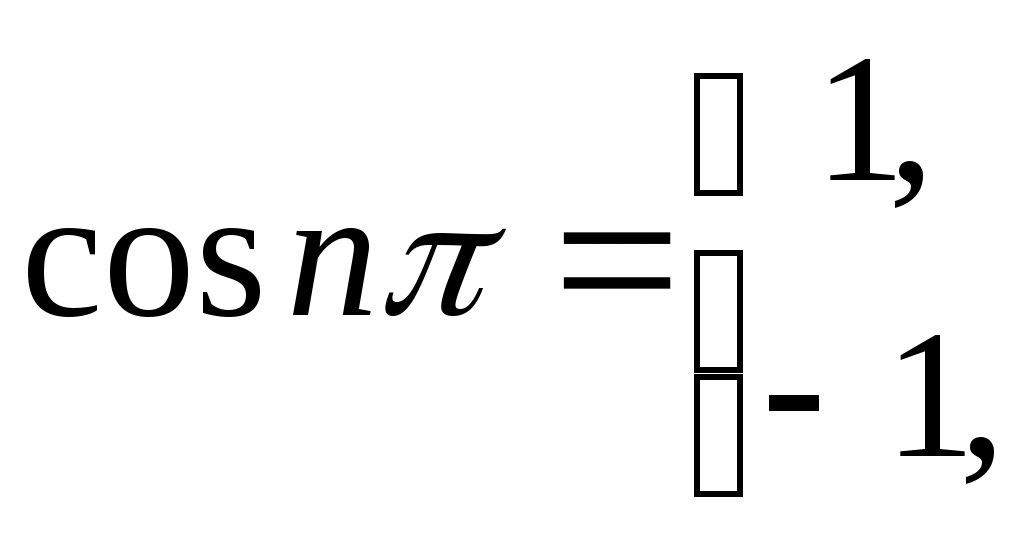
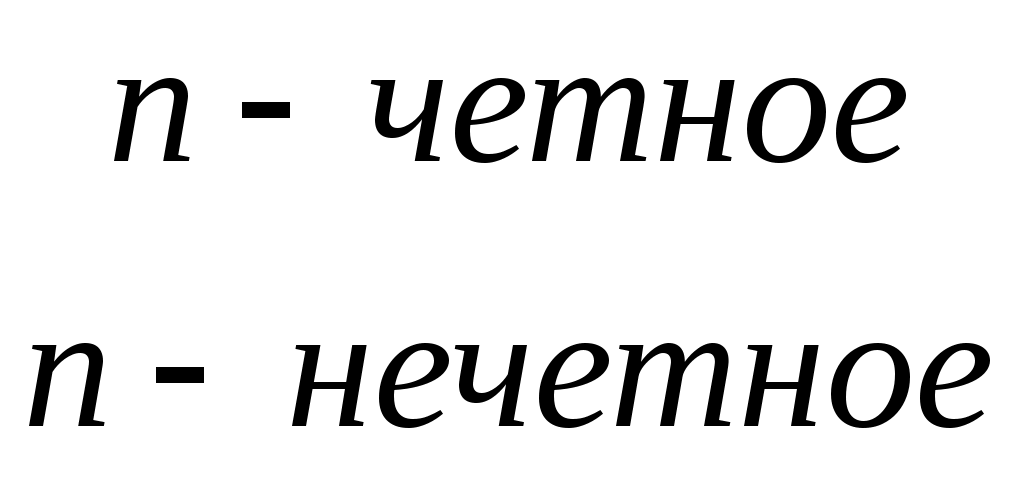, то 
. Тогда
.
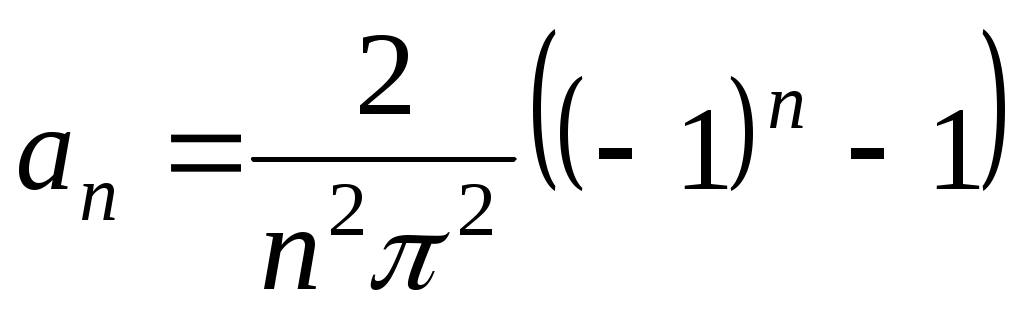Далее,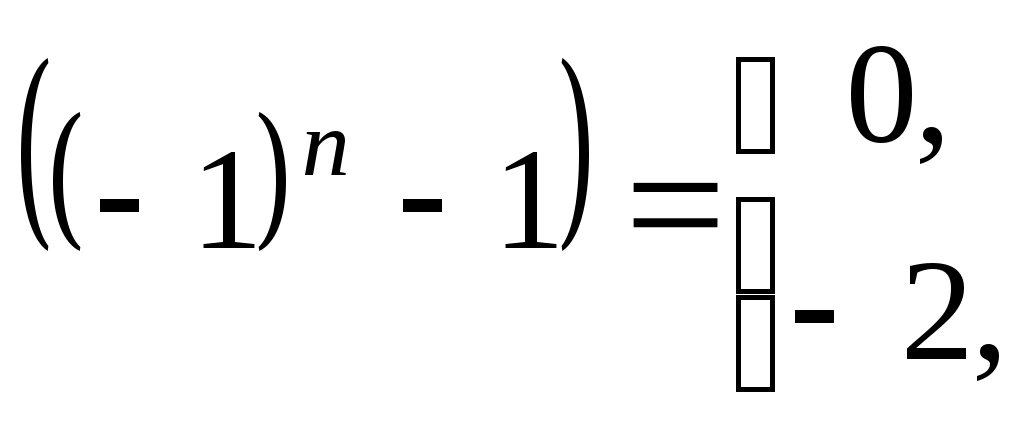
, 
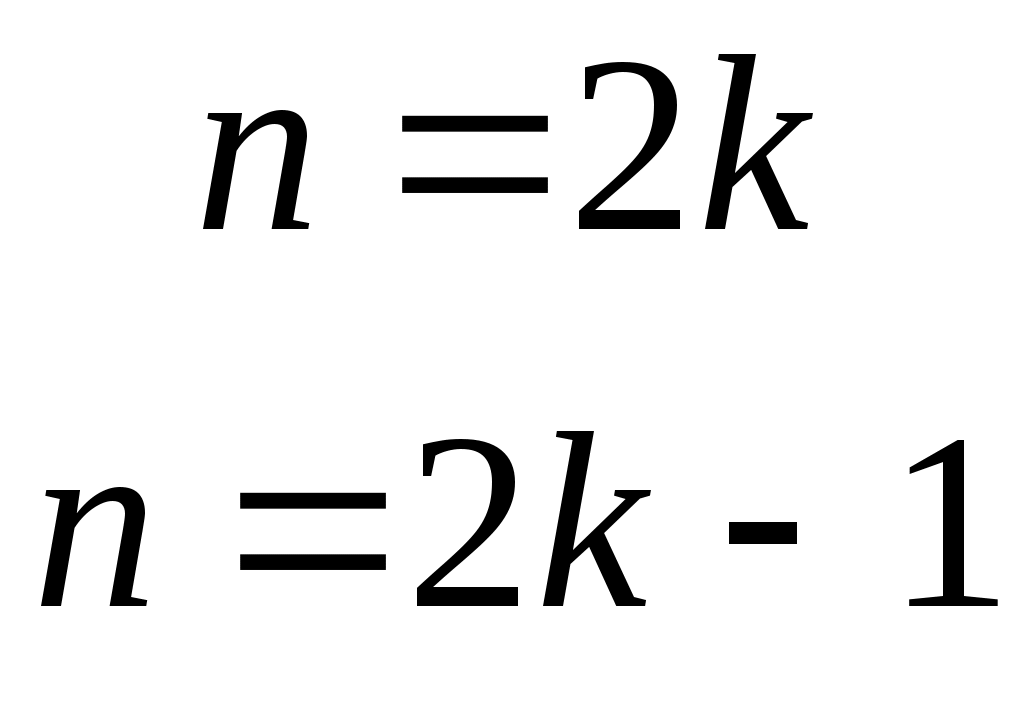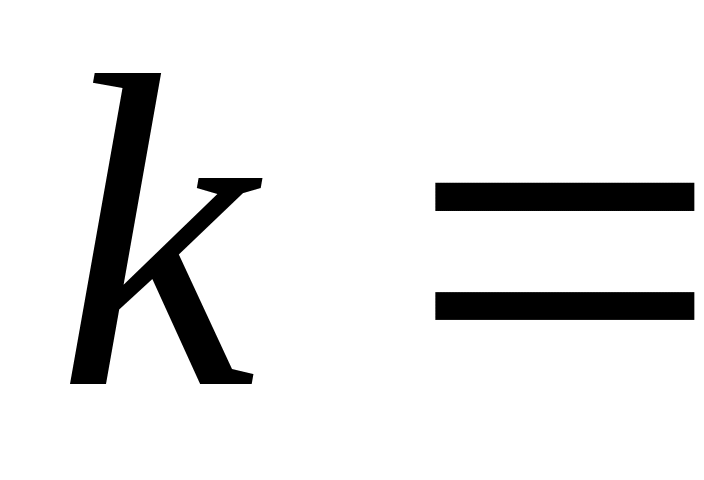1, 2, … . и, следовательно, коэффициенты 
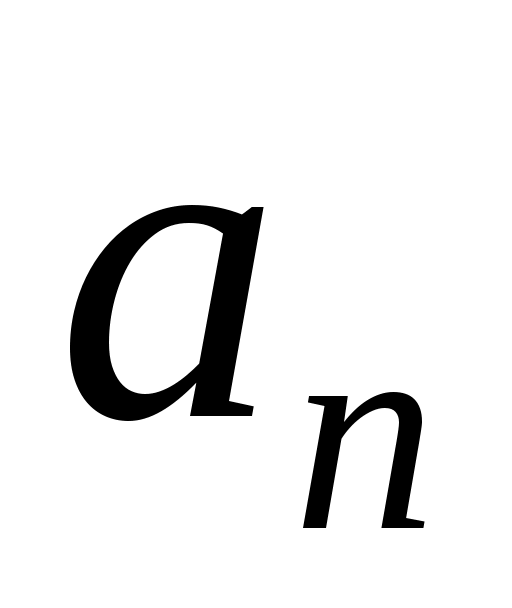имеют ненулевые значения только при нечетных , т.е. при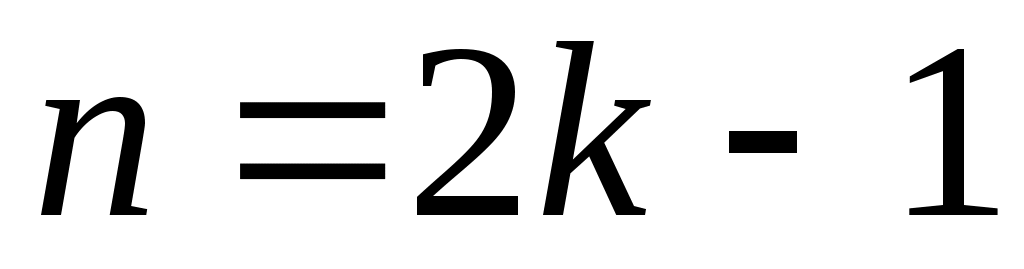 
. Таким образом,
,
.
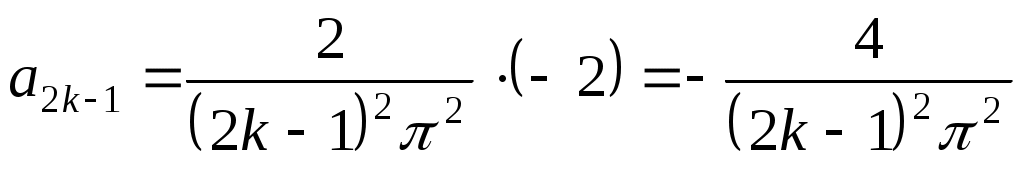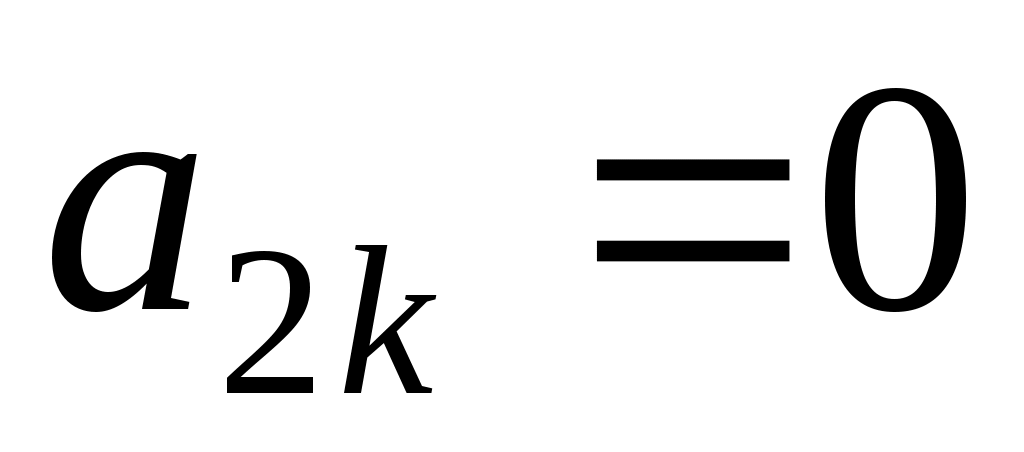Подставляем найденные коэффициенты в формулу (а):
.
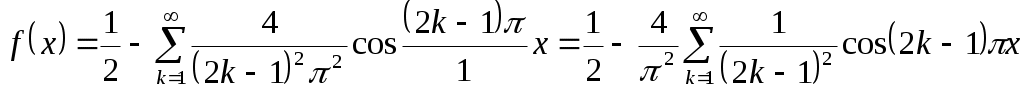Ответ: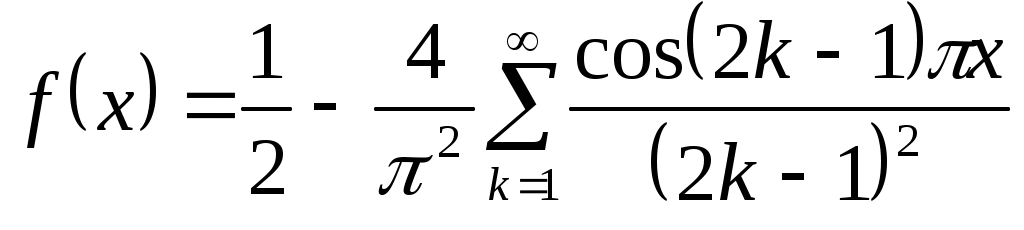
, 
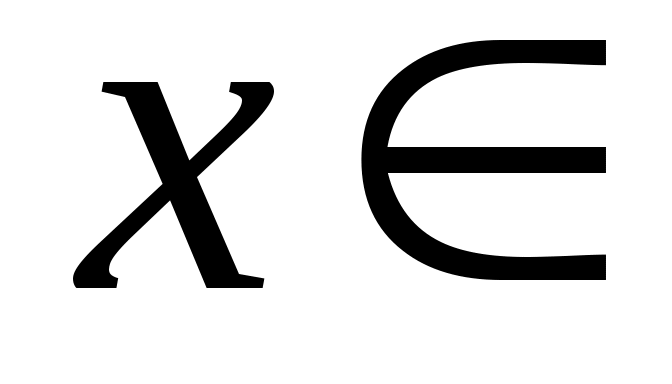(-1; 1).
Литература
1. Письменный, Д.Т. Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. – М.: Айрис-пресс, 2005. – 604 с.
2. Пискунов, Н.С. Дифференциальное и интегральное исчисление: учебное пособие для втузов: в 2 т. Т. 2 / Н. С. Пискунов.– Изд. стер. – М.: Интеграл-Пресс, 2001.– 544 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах: в 2 ч. Ч.2. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова.– М.: ОНИКС 21 век, Мир и образование, 2003. – 304 с.
4. Шипачев, В.С. Высшая математика / В.С. Шипачев. – М.: Высшая школа, 2007. – 479 с.
5. Шипачев, В.С. Задачник по высшей математике / В.С. Шипачев. – М.: Высшая школа, 2001. – 304 с.
6. Котов, А.А. Числовые ряды. Функциональные степенные ряды / А.А. Котов. – Мурманск: МГТУ, 2003. – 92 с.
0, 1, 2, …Полученный ряд оказался знакочередующимся. Поэтому используем то же самое условие обеспечения заданной точности, что и в предыдущей задаче:
. (а)Здесь
, поэтому минимально необходимое
находим из условия , или : , .Из последнего вытекает, что для обеспечения заданной точности достаточно просуммировать первые шесть членов ряда:
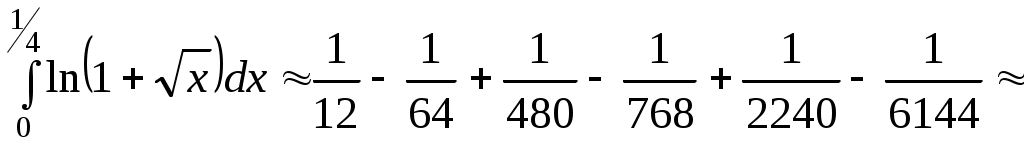
.Ответ:
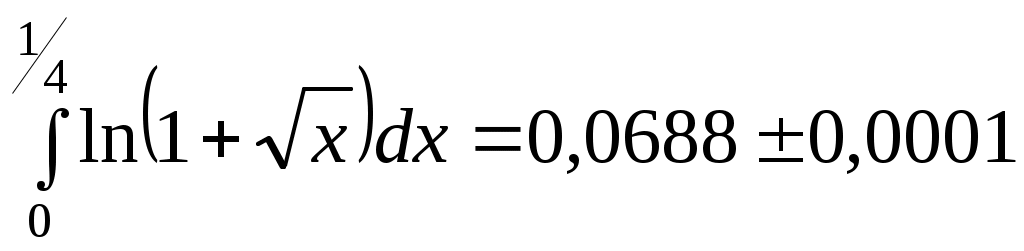.Задача 6. Данную функцию
разложить в ряд Фурье в заданном интервале.
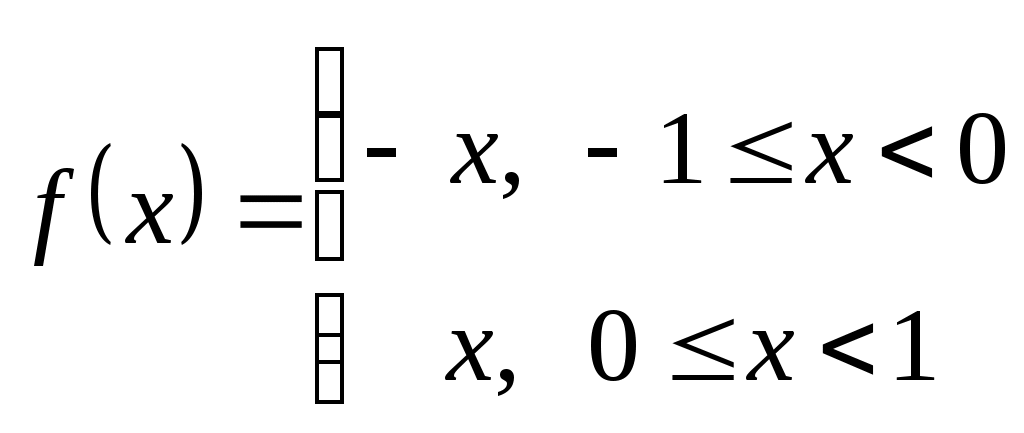, (-1, 1).Легко убедиться, что в заданном интервале функция непрерывна и, следовательно, может быть представлена своим рядом Фурье в смысле теоремы Дирихле. Кроме того, в рассматриваемом интервале она четная, поэтому ее ряд Фурье должен содержать только четные тригонометрические функции, т.е. косинусы. На этих основаниях записываем:
, . (а)Находим коэффициенты.
.
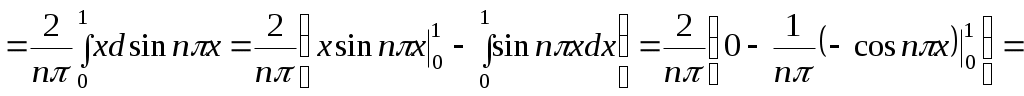
.Т.к.
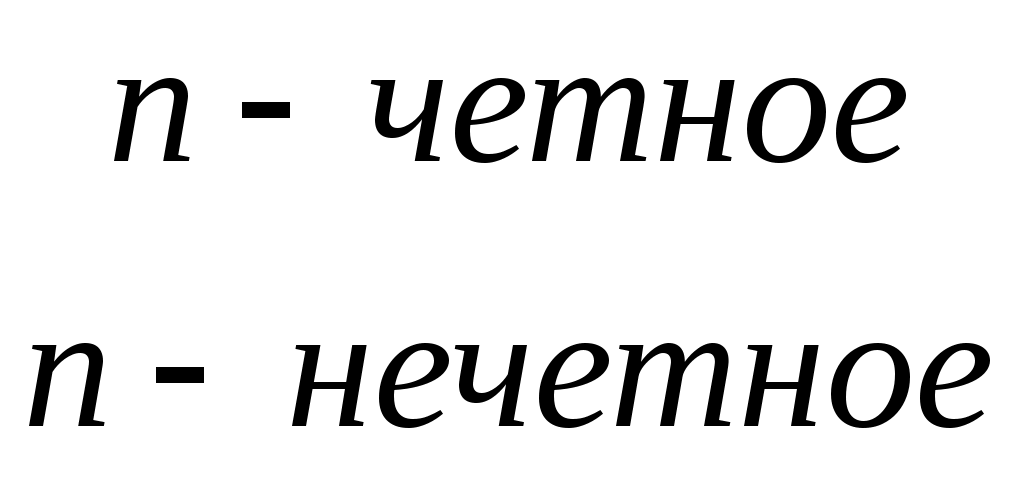, то . Тогда . Далее,
, 1, 2, … . и, следовательно, коэффициенты имеют ненулевые значения только при нечетных , т.е. при . Таким образом, , .Подставляем найденные коэффициенты в формулу (а):
.Ответ:
, (-1; 1).Литература
1. Письменный, Д.Т. Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. – М.: Айрис-пресс, 2005. – 604 с.
2. Пискунов, Н.С. Дифференциальное и интегральное исчисление: учебное пособие для втузов: в 2 т. Т. 2 / Н. С. Пискунов.– Изд. стер. – М.: Интеграл-Пресс, 2001.– 544 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах: в 2 ч. Ч.2. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова.– М.: ОНИКС 21 век, Мир и образование, 2003. – 304 с.
4. Шипачев, В.С. Высшая математика / В.С. Шипачев. – М.: Высшая школа, 2007. – 479 с.
5. Шипачев, В.С. Задачник по высшей математике / В.С. Шипачев. – М.: Высшая школа, 2001. – 304 с.
6. Котов, А.А. Числовые ряды. Функциональные степенные ряды / А.А. Котов. – Мурманск: МГТУ, 2003. – 92 с.