Файл: Отчет по лабораторной работе 4 по дисциплине Теория автоматического управления.docx
Добавлен: 07.11.2023
Просмотров: 44
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «СЕВАСТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт информационных технологий
и управления в технических системах
Кафедра
«Информатика и управление в технических системах»
ОТЧЕТ
по лабораторной работе №4
по дисциплине «Теория автоматического управления»
Вариант № 3
Выполнил:
ст. группы УТС/б-19-2-о
Димин М.Э.
Принял:
доцент кафедры ИУТС
Карапетьян В.А.
Севастополь
2021
1 Цель работы
Исследование методов и средств пакета имитационного моделирования Simulink для формирования, анализа и моделирования различных типов моделей линейных стационарных систем автоматического управления.
2 Постановка задачи
Первая часть работы:
а) ознакомиться с содержанием второго раздела методических указаний и выполнить все иллюстративные примеры, приведенные в нём;
б) при выполнении примеров необходимо научиться использовать различные источники и приёмники сигналов; сформировать векторные сигналы из скалярных и извлекать скалярные сигналы из векторных; изменять точность расчётов и т.д.
Вторая часть работы:
| № вар. | R Ом | L мГн |   |   |   |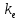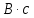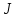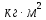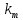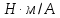
| 3 | 0.945 | 45.9 | 0.341 | 0.14 | 0.261 |
а) сформировать Simulink-модель ДПТ по скорости и провести моделирование отдельно при управляющем воздействии, отдельно при возмущающем воздействии и при их совместном действии. Выполнить данный пункт для двух форм моделей ДПТ в виде ПФ. Графически сравнить результаты моделирования;
б) провести моделирование САУ скоростью ДПТ с П- и ПИД-регулятором. Определить характер реакций системы на входные воздействия по графикам, построенным на основе данных, переданных из пакета Simulink в рабочую область MatLab (Workspace) через блок «To Workspace» библиотеки «Sinks»;
в) провести моделирование следящей САУ с ПД-регулятором по углу по схеме. В качестве задающего воздействия принять угол в 5 градусов. Определить время отработки задающего воздействия. Проанализировать влияние внешнего возмущения МН на качество и точность отработки задающего воздействия.
г) привести последовательность графо-аналитических (структурных) преобразования и получить ПФ рассматриваемой САУ по управлению и возмущению. Решить аналогичную задачу с помощью средства MatLab;
д) построить Simulink-модель ДПТ в форме пространства состояний на основе уравнений (3.9 методических указаний). Уравнение выхода сформировать с учётом возможности измерения всех переменных состояния: угла поворота
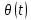вала, угловой скорости вращения 
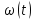вала и тока в якорной цепи 
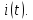Управляющее 
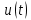и возмущающее 
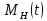воздействия организовать в один вектор внешних воздействий. Провести моделирование следящей САУ ДПТ по углу, начальные условия принять нулевыми. Дополнительно провести моделирование данной САУ и построить собственное движение системы для случая начального отклонения по углу, равного 2 градусам.3 Ход работы
3.1 ЧАСТЬ 1
Таблица 3.1.1 – Код программы первой части работы.
| % Вариант 3 clc; clear; close; %% Y_s=[0 1; 2 2]; a = 6; b = 1; c = 0.2; |
Иллюстративный пример пункта 2.1 методических указаний представляет собой схему, изображённую на рисунке 3.1.2. Для схемы изменено время моделирования, параметры передаточной функции (ПФ), шаг выдачи результата.
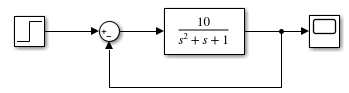
Рисунок 3.1.1 – Simulink-модель иллюстративного примера 2.1.
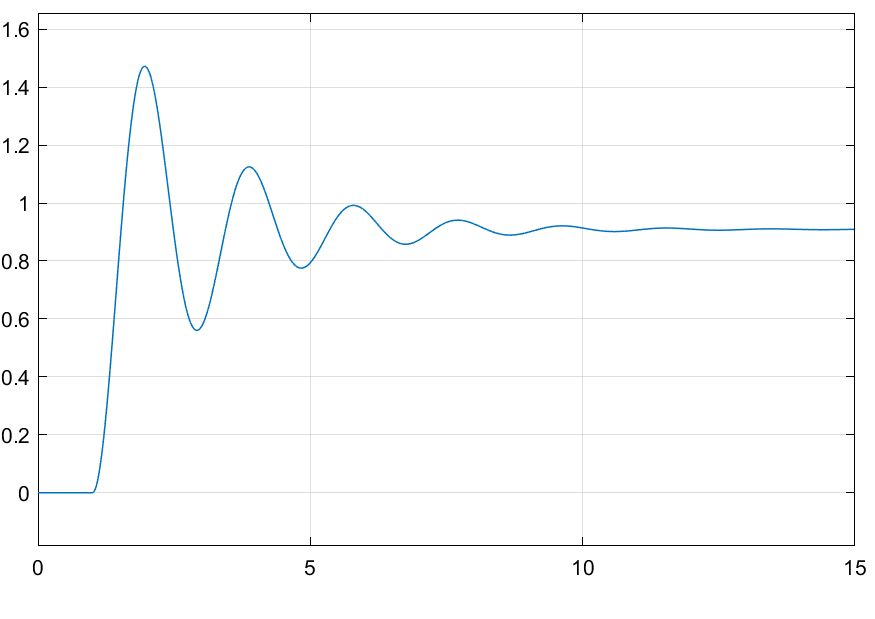
Рисунок 3.1.2 – Реакция модели на функцию Хэвисайда.
Для схемы 3.1.1 посредством блока «To file» библиотеки Simulink сделан вывод в mat-файл «Dimin_data», из которого блоком «From file» производится изъятие значений.
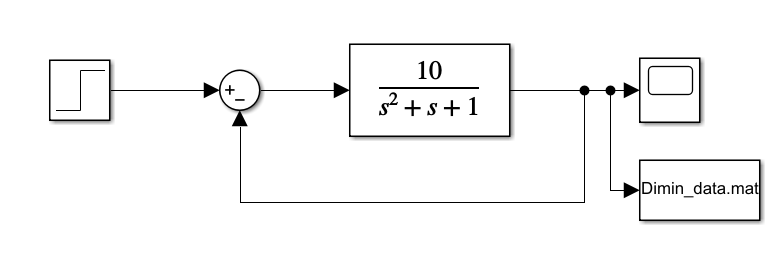
Рисунок 3.1.3 – Simulink-модель с записью значений в mat-файл.
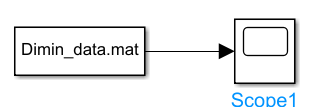
Рисунок 3.1.4 – Simulink-модель с чтением значений из mat-файл.
Рисунок 3.1.5 – График, построенный по значениям, взятым из файла.
В иллюстративном примере выше график результата моделирования был построен с помощью осциллографа. В примере пункта 2.5.2 построение графика происходит с помощью блока XY Graph.
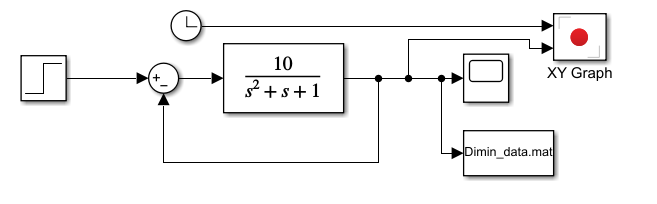
Рисунок 3.1.6 – Simulink-модель с выводом в XY Graph.
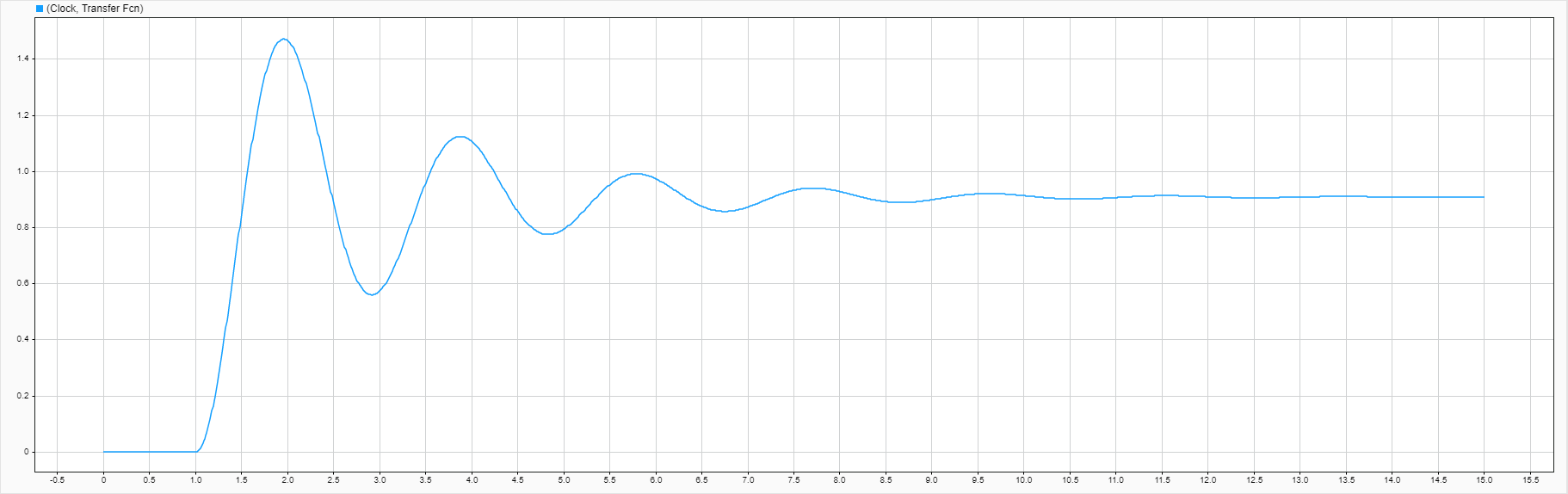
Рисунок 3.1.7 – График, созданный блоком XY Graph.
Пример интегрирования ступенчатого сигнала при интеграторах с подачей начального значения через внутренний параметр -2.2 (рис. 3.1.8(a)) и внешний порт (рис. 3.1.8 (b)).
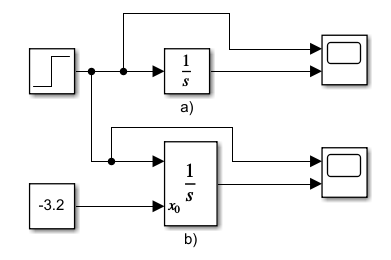
Рисунок 3.1.8 – Simulink-модель с интеграторами: а) с внутренним значением начальных условий; б) с внешним.
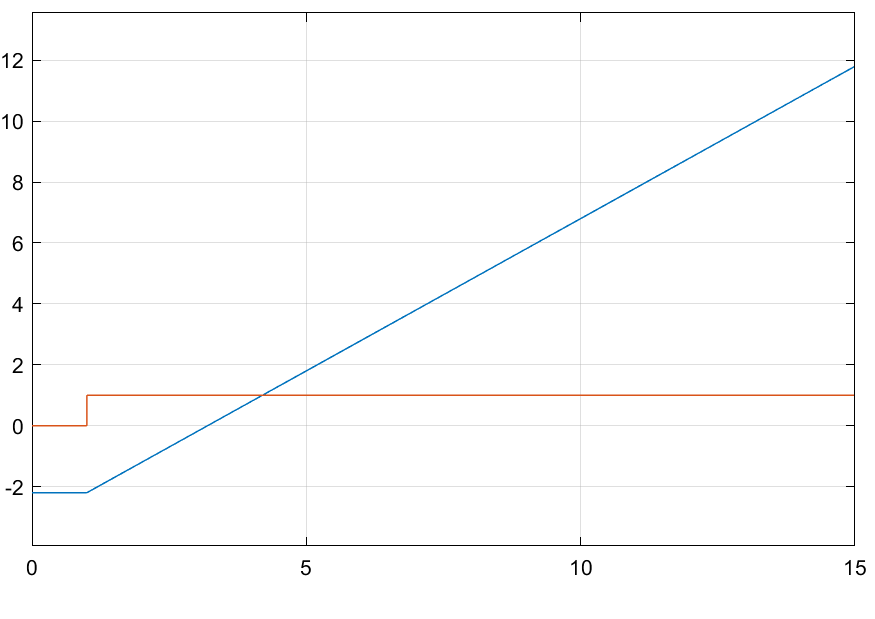
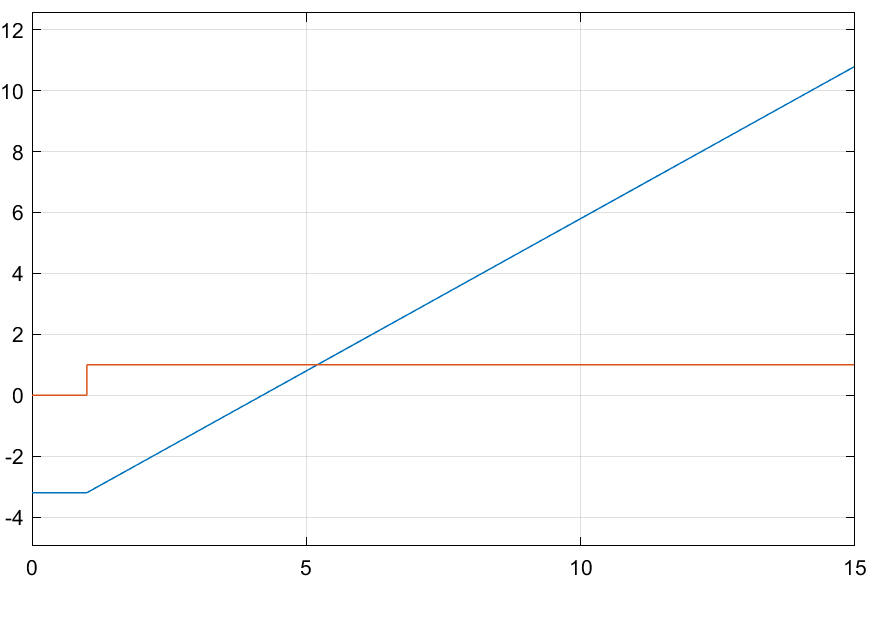
Рисунок 3.1.9 – Результаты работы схемы с внутренним, внешним интеграторами соответственно.
Передаточные функции:
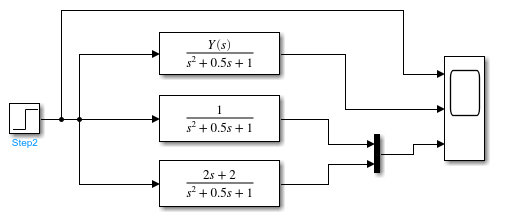
Рисунок 3.1.10 – Simulink-модель ПФ и её скалярного варианта.
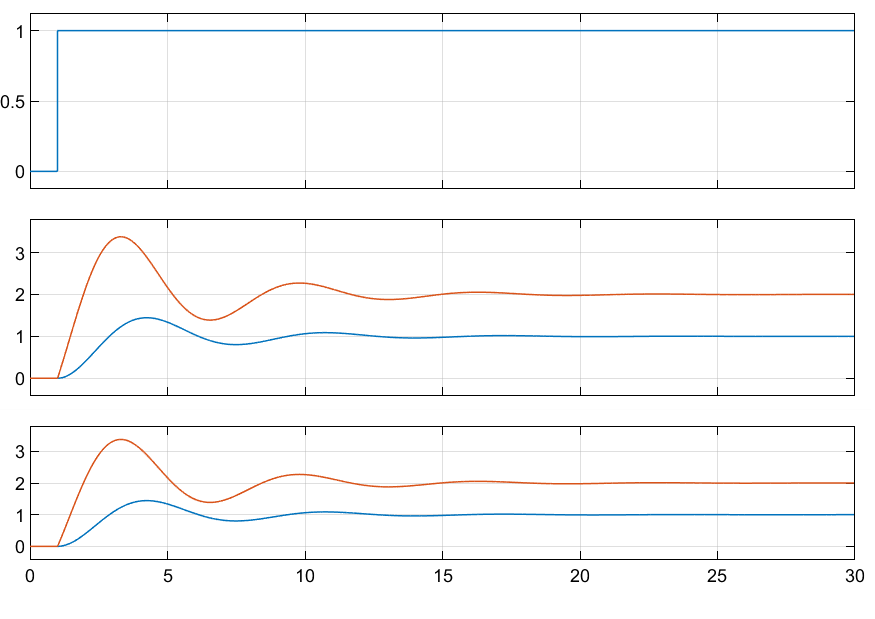
Рисунок 3.1.11 – Результаты моделирования ПФ и её скалярного варианта.
Использование переменных для задания параметров блоков. Вывод результатов моделирования в Workspace (рис. 3.1.12).
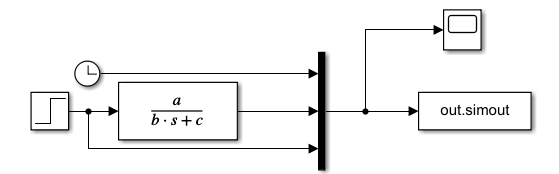
Рисунок 3.1.12 – Simulink-модель и вывод её значений в Workspace.
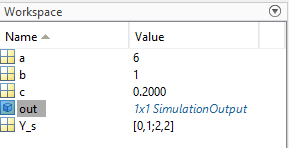
Рисунок 3.1.13 – Переменная out, созданная в Workspace.
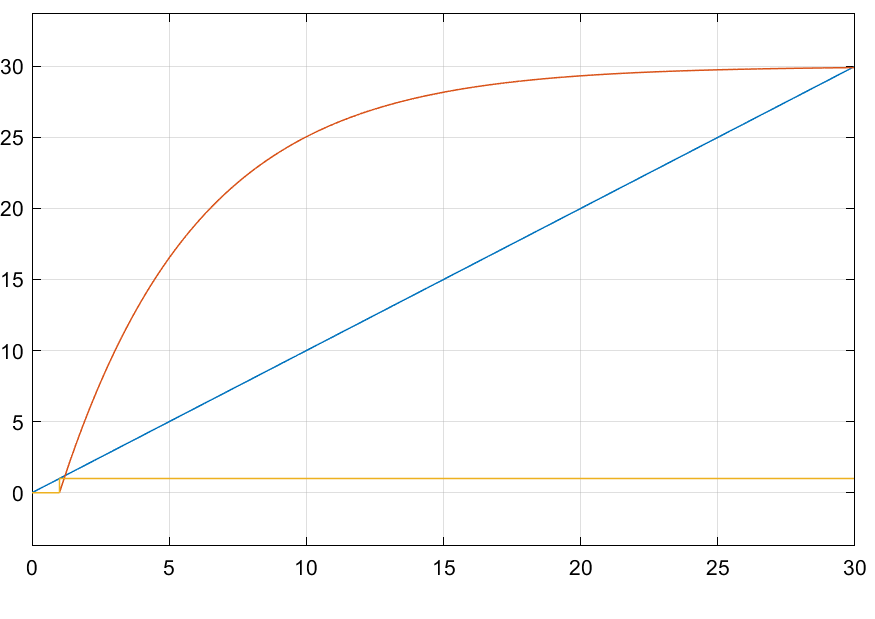
Рисунок 3.1.14 – Результаты моделирования ПФ и её скалярного варианта
3.2 ЧАСТЬ 2
Таблица 3.2.1 – Код программы второй части работы.
| % Вариант 3 clc; clear; close; %% Part 1 Y_s=[0 1; 2 2]; a = 6; b = 1; c = 0.2; %% Part 2 % а) L = 0.0459; R = 0.945; km = 0.261; ke = 0.341; J = 0.14; % б) Kp = 30,9; Ki = 94,7; Kd = 1,4; %% subplot(2,1,1); plot(out.P_regular); title('График моделирования ДПТ с P-регулятором'); grid on; xlabel('Время'); ylabel('Угловая скорость вращения вала'); subplot(2,1,2); plot(out.PID_regular); title('График моделирования ДПТ с PID-регулятором'); grid on; xlabel('Время'); ylabel('Угловая скорость вращения вала'); %% в) L = 0.0459; R = 0.945; km = 0.261; ke = 0.341; J = 0.14; Kp = 1.03; Kd = 2.46; %% subplot(2,1,1); plot(out.nP_regular); title('График моделирования следящей САУ ДПТ с P-регулятором'); grid on; xlabel('Время'); ylabel('Угловая скорость вращения вала'); subplot(2,1,2); plot(out.PD_regular); title('График моделирования следящей САУ ДПТ с PD-регулятором'); grid on; xlabel('Время'); ylabel('Угловая скорость вращения вала'); %% г) [A,B,C,D] = linmod('TAU_Lab4_sim_Part_II_g',[0 0]); tf(ss(A,B,C,D)) |
а) Формирование Simulink-модель ДПТ по скорости и моделирование отдельно при управляющем, возмущающем и совместном воздействии.
Общее уравнение, описывающее модель ДПТ, имеет вид:
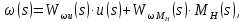
где
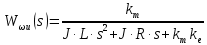– ПФ ДПТ по управляющему воздействию;
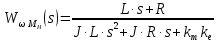– ПФ ДПТ по возмущению.Или в одном из стандартных видов:
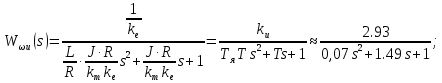
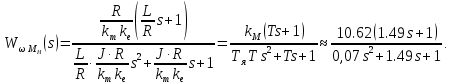
В выше представленных выражениях для ПФ ДПТ по управлению и возмущению введены параметры:
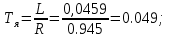
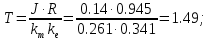
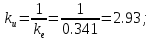
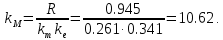
Соответственно Simulink-модель ДПТ в терминах ПФ приведена на рисунке 3.2.1.
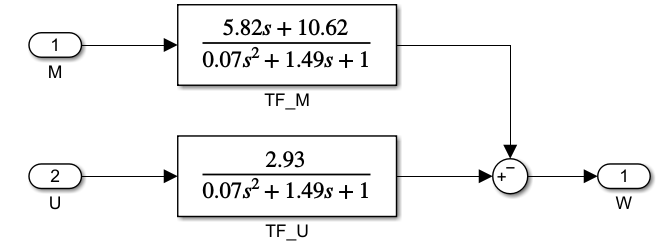
Рисунок 3.2.1 – Simulink-модель ДПТ в терминах ПФ.
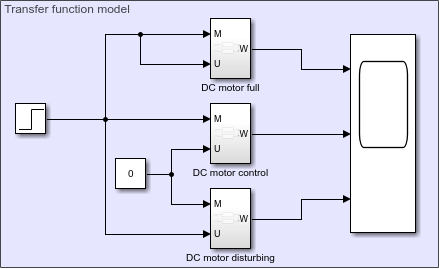
Рисунок 3.2.2 – Simulink-модель ДПТ в терминах ПФ для общего, возмущающего и управляющего воздействий.
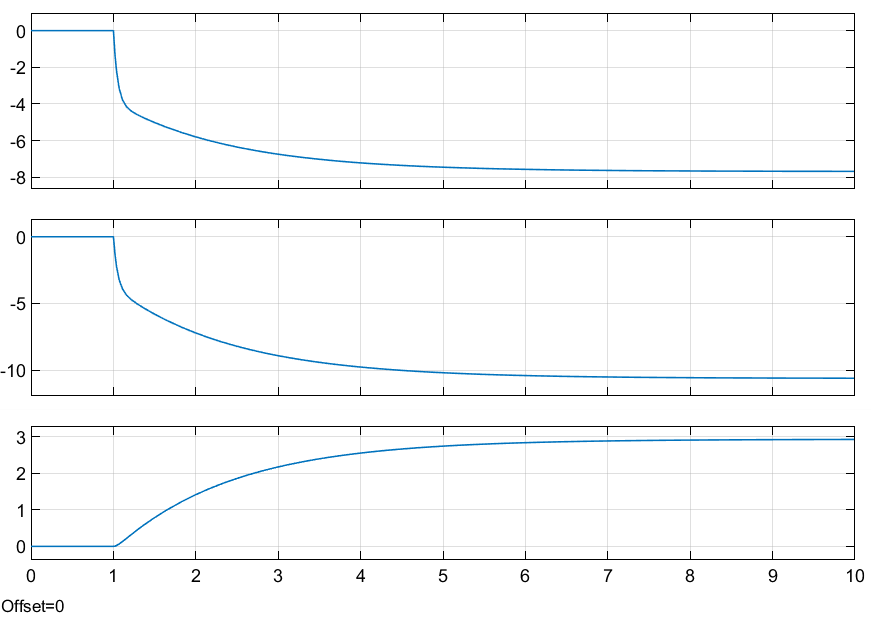
Рисунок 3.2.3 – Результаты моделирования модели в виде ПФ.
Модель ДПТ в терминах изображений переменных пространства состояний представлена на рисунке 3.2.4.
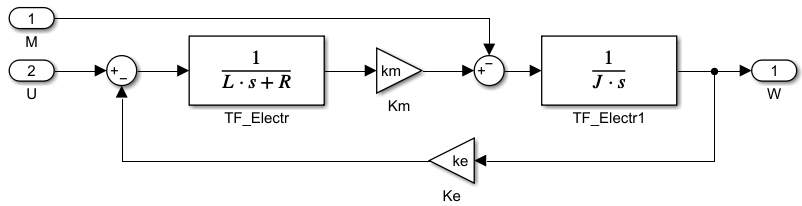
Рисунок 3.2.4 – Simulink-модель ДПТ скоростного контура.
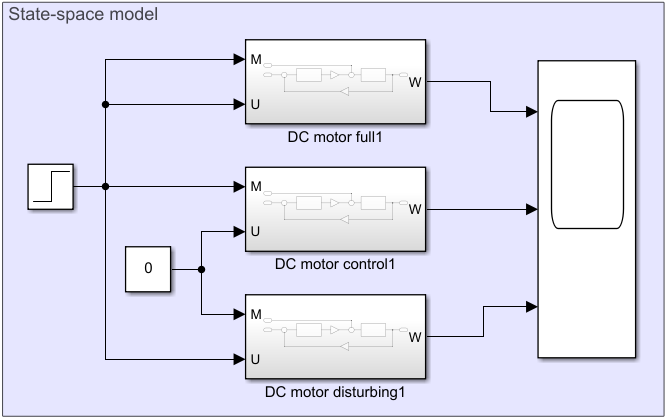
Рисунок 3.2.5 – Simulink-модель ДПТ в терминах пространства состояний для общего, возмущающего и управляющего воздействий.
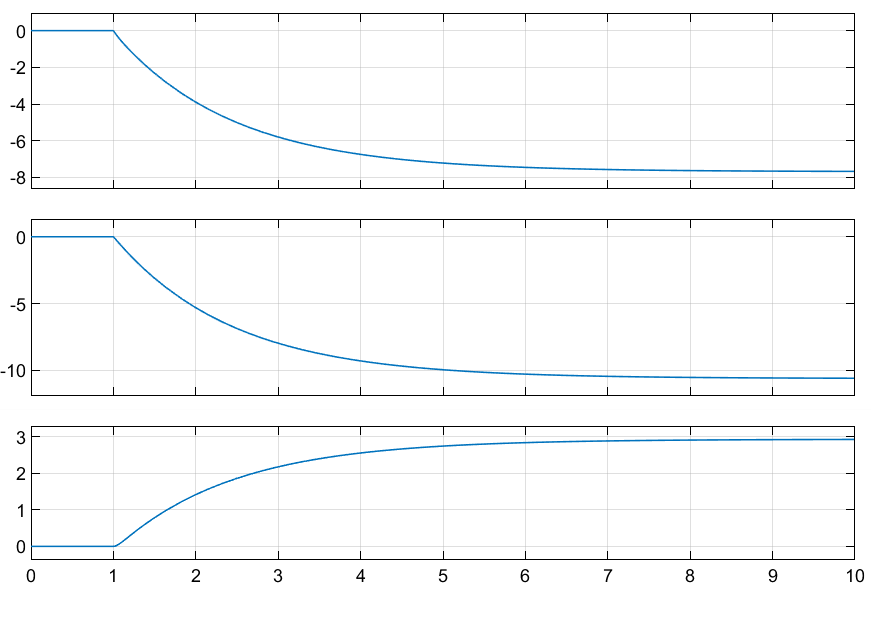
Рисунок 3.2.6 – Результаты моделирования модели в пространстве состояний.
б) Моделирование САУ скоростью ДПТ с П- и ПИД-регулятором. Определение характера реакций системы на входные воздействия по графикам, построенным на основе данных, переданных из пакета Simulink в рабочую область MatLab (Workspace) через блок «To Workspace» библиотеки «Sinks».
Рисунок 3.2.7 – Simulink-схема САУ скорости с P-регулятором.
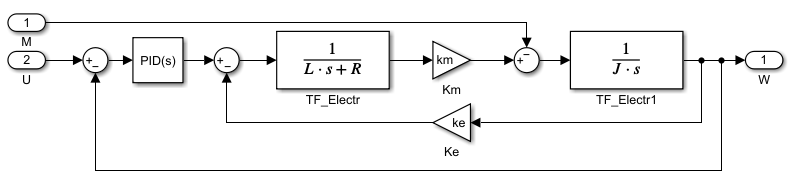
Рисунок 3.2.8 – Simulink-схема САУ скорости с PID-регулятором.