ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа «Проведение кластерного анализа двум\ способами».
Исходные данные: воспользуйтесь базой данных, которую вы собирали для расчета многомерной средней величины (относительные показатели).
Цель исследования: провести кластерный анализ по относительным показателям, характеризующим выбранную сферу (здравоохранение, образование в разрезе субъектов федерации, правоохранительную деятельность и т.п.) в пакете Statistica двумя методами (иерархическим кластерным методом, методом k-средних. Сделать выводы.
Ход выполнения работы
Таблица 1 – Исходные данные
| N/ N | Относительный показатель 1 | Относительный показатель 2 | Относительный показатель 3 | Относительный показатель 4 | Относительный показатель 5 | Относительный показатель 6 |
| 1 | | | | | | |
| 2 | | | | | | |
| 3 | | | | | | |
| 4 | | | | | | |
| 5 | | | | | | |
| 6 | | | | | | |
| 7 | | | | | | |
| 8 | | | | | | |
| 9 | | | | | | |
| 10 | | | | | | |
| … | … | … | … | … | … | … |
Загрузите полученные данные в программу для проведения кластерного анализа.
1 метод – иерархический кластерный анализ.
Основа кнопочного меню для проведения кластерного анализа представлена ниже:
Иерархический кластерный анализ (в англоязычной версии 13.5)
1.
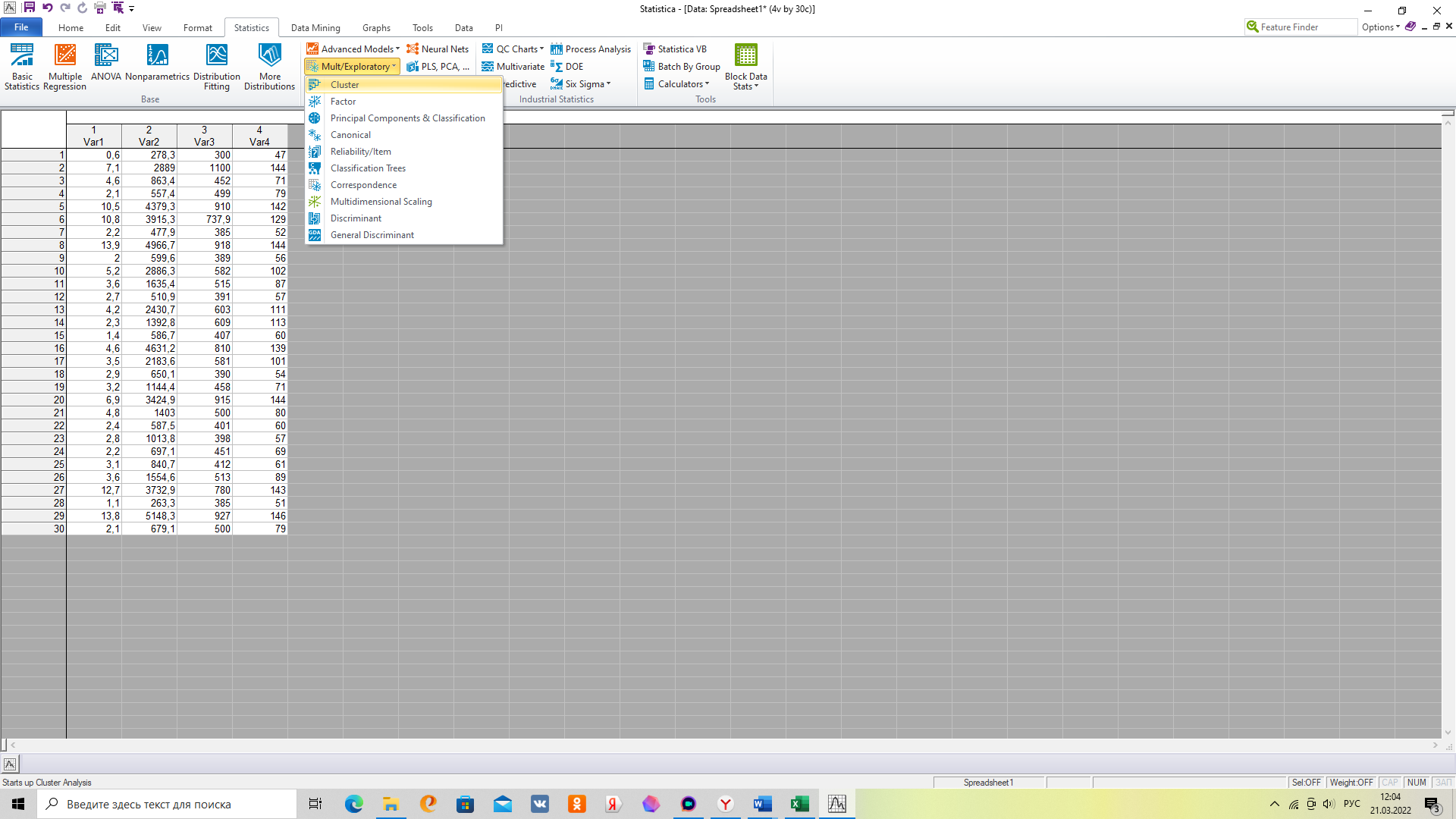
2. Выбираем метод иерархической кластеризации
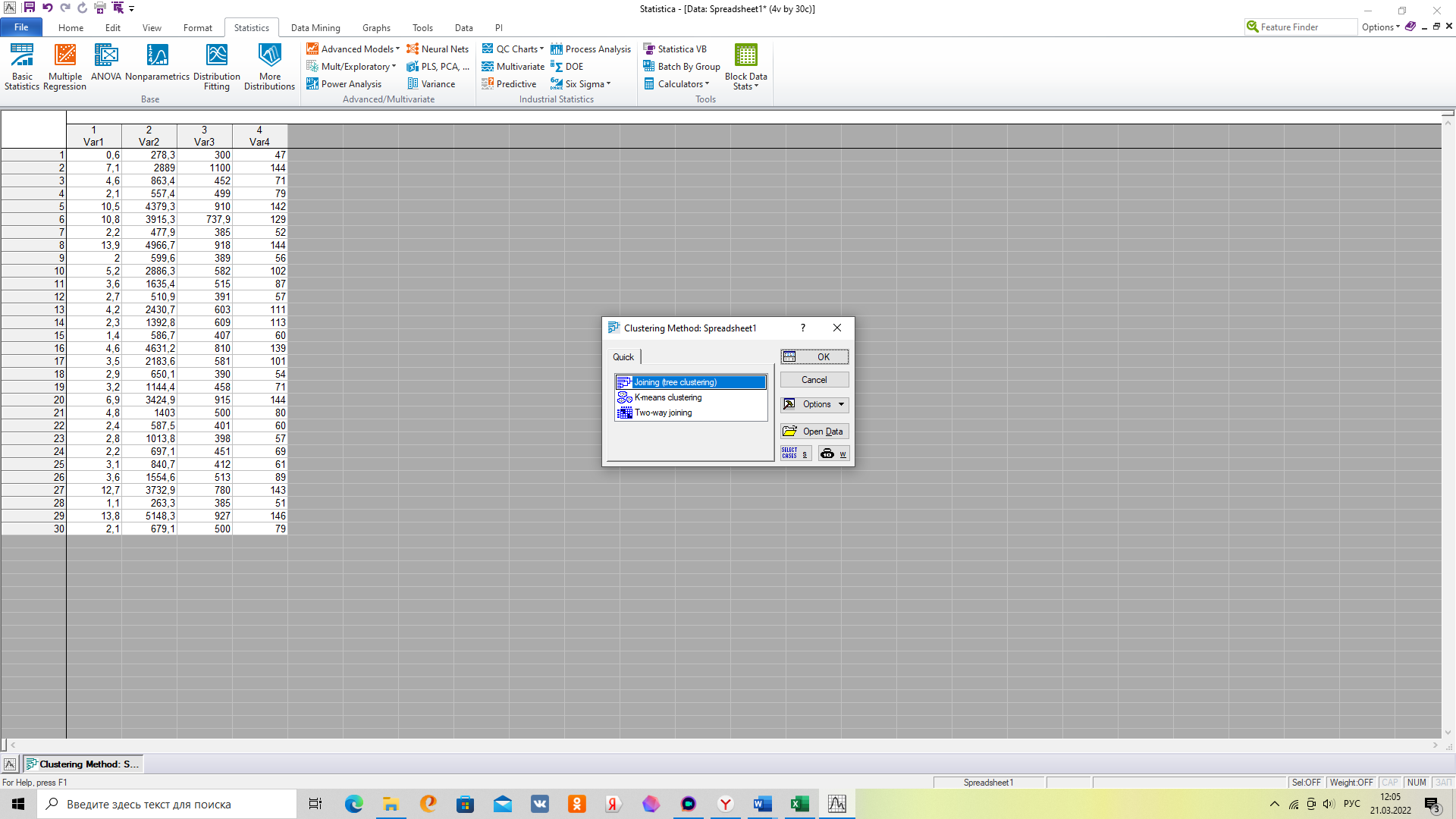
3. Выбираем исходные данные в открывшейся вкладке «Variables»
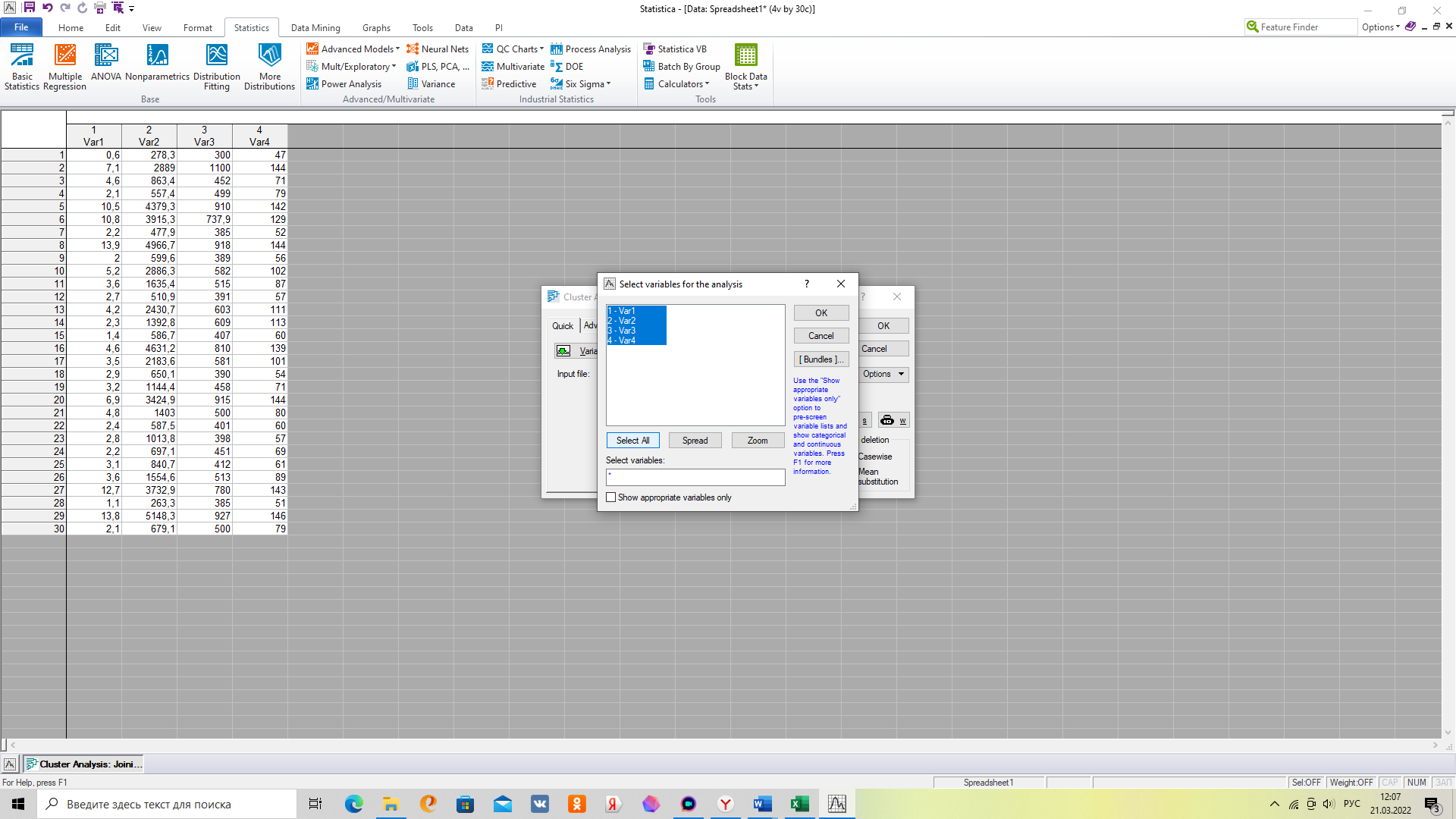
4. Во вкладке «Advanced» не забудьте указать, что наблюдения представлены в строчках.
5. Раскрываем дендрограмму распределения по кластерам
Именно на основе схемы объединения (дендрограммы) при иерархическом кластерном анализе устанавливается оптимальное разбиение (число кластеров и их состав).
Для этого следует в крайнем левом столбце схемы объединения , где фиксируется на каждом шаге значение функции близости , установить ее резкий скачок. Предыдущий этому скачку шаг ( итерация) рассматривается предположительно как оптимальное разбиение. Смотрим какие элементы объединены на этой итерации. Запишем их номера. Смотрим предыдущий шаг – элементы ( объекты) на этом шаге повторяют элементы оптимального разбиения. Если повторяют- это не самостоятельный кластер, если не повторяют – это второй самостоятельный кластер, запишем его номера. Переходим к следующей итерации ( шагу) и повторяем туже процедуру. Так находим все самостоятельные кластеры и их состав.
Аналогично распределение по кластерам можно смотреть не на графике, а в таблице «Amalgamation Schedule»
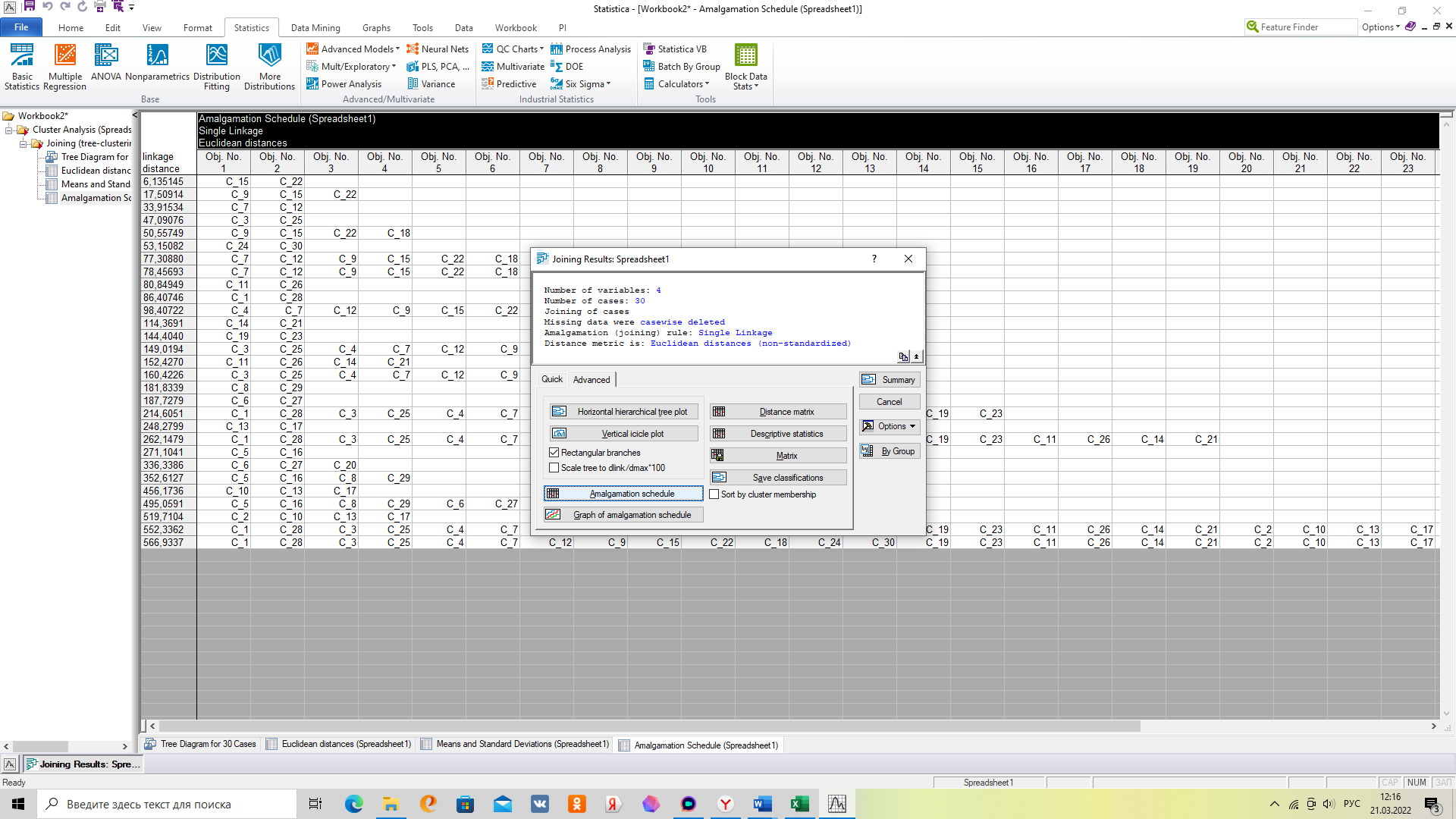
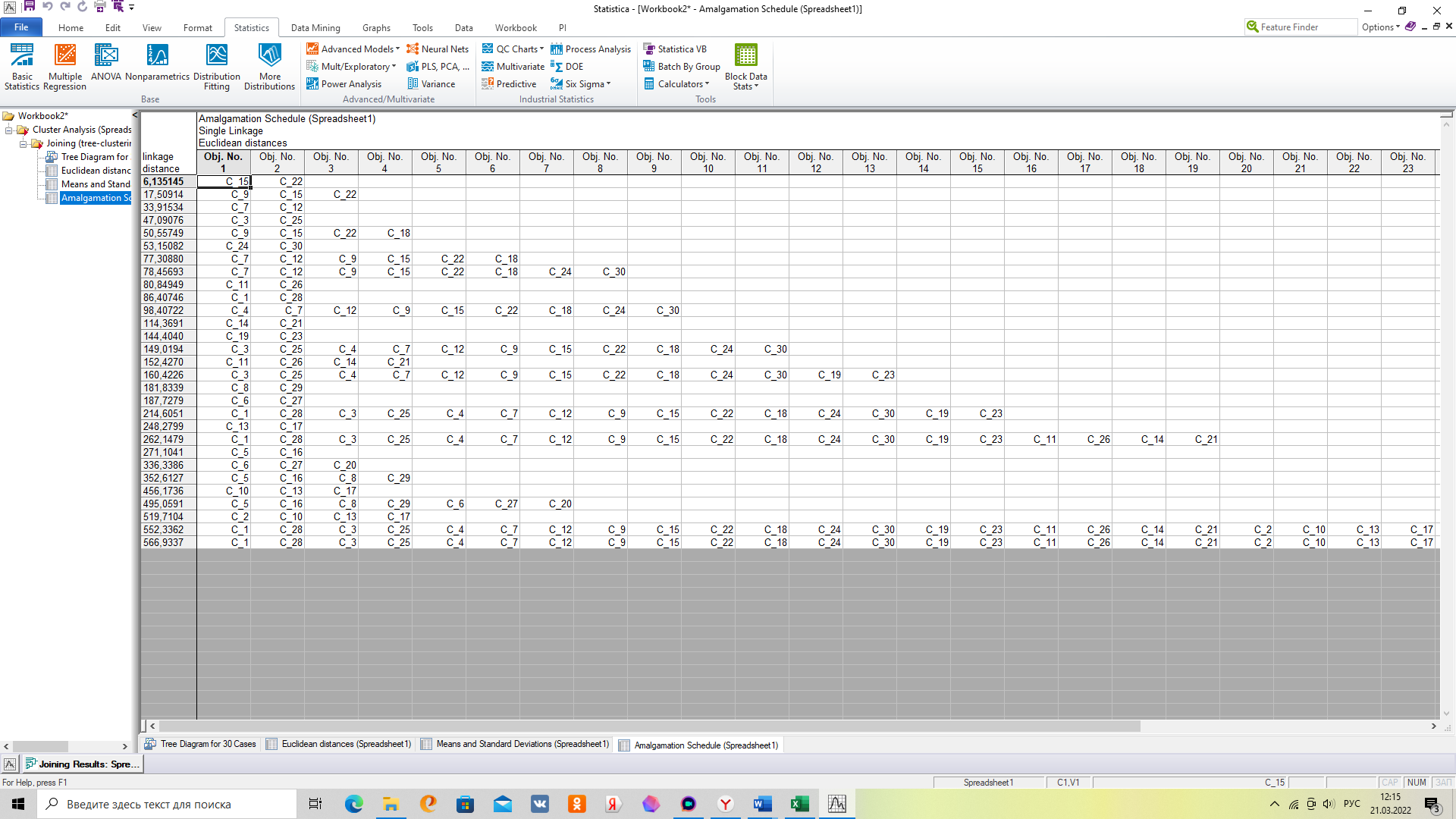
В заключение метода 1 надо установить состав кластеров и равномерность распределения.
Иерархический кластерный анализ (в старых версиях)
-
Statistics - статистика -
Mult/ Exploratory-многомерный разведочный анализ -
Cluster – кластерный анализ -
Joning (tree clucterig)- иерархический кластерный анализ -
Raw data - необработанные данные -
Variables -переменные ( обозначить переменные включенные в анализ) -
Raw data – необработанные данные -
Gluster (выбрать Cases (rows) - наблюдения строки -
Amalgamation ( linkage) rule - правило объединения – выбрать Single linkage - одиночная связь ближний сосед., хотя посмотреть и другие правила объединения ( о них в лекции) -
Distance measure - мера расстояния - выбрать Euclidean distances – Евклидово расстояние. -
Horizontal tree plot -горизонтальная дендрограмма объединения – посмотреть процесс последовательного объединения -
Advanced – дополнительно -
Amalgamation schedule – схема объединения.
2 метод - Кластерный анализ методом К- средних
Анализ с использованием метода k-средних позволит разделить совокупность анализируемых организаций на низшую, среднюю и высшую группы.
Основа кнопочного меню для проведения кластерного анализа представлена ниже:
Кластерный анализ методом к-средних (в англоязычной версии 13.5)
1.

2. Выбираем метод иерархической кластеризации
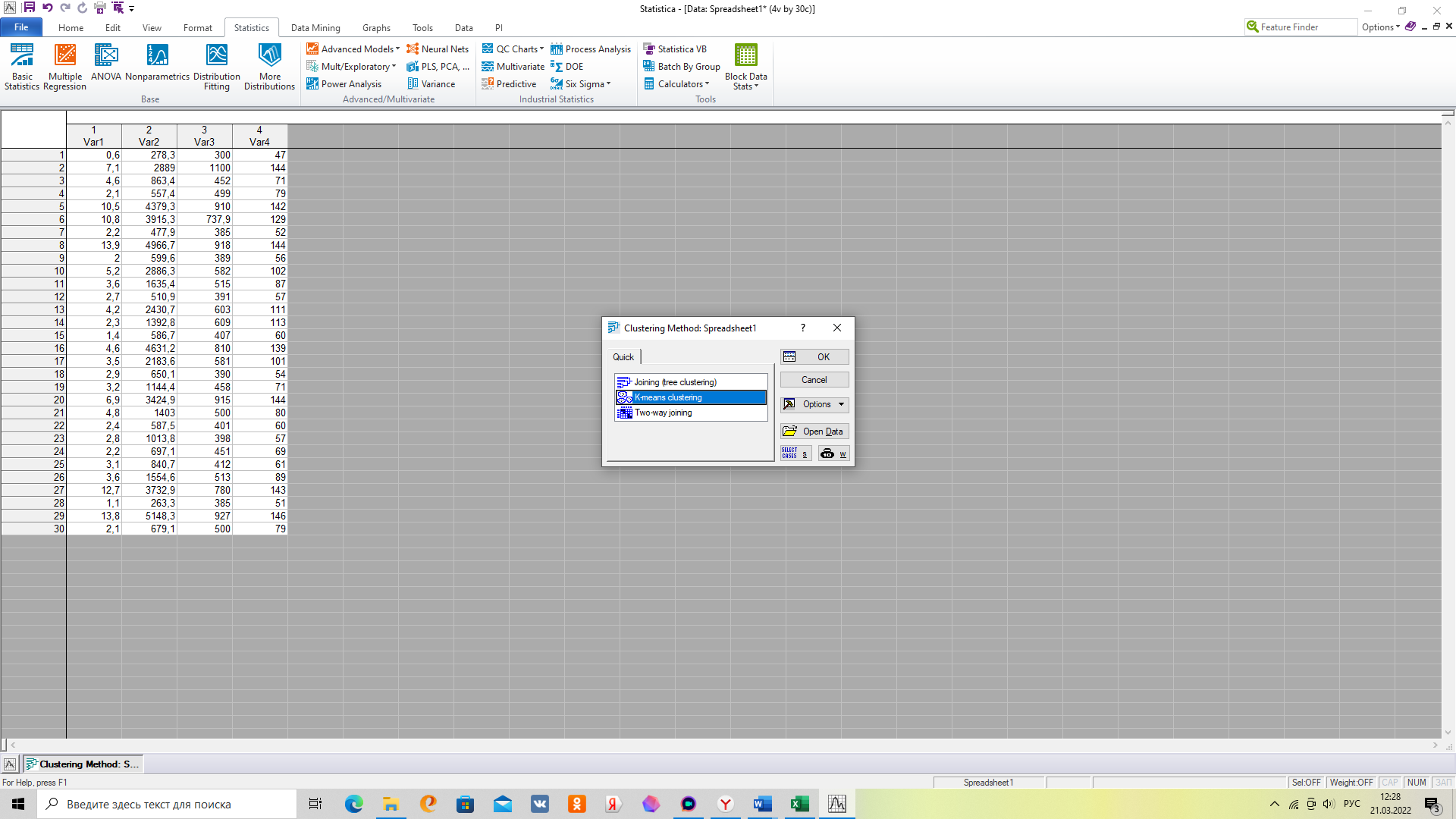
3. Выбираем исходные данные в открывшейся вкладке «Variables»

4. Во вкладке «Advanced» не забудьте указать, что наблюдения представлены в строчках и указать количество кластеров – 3.
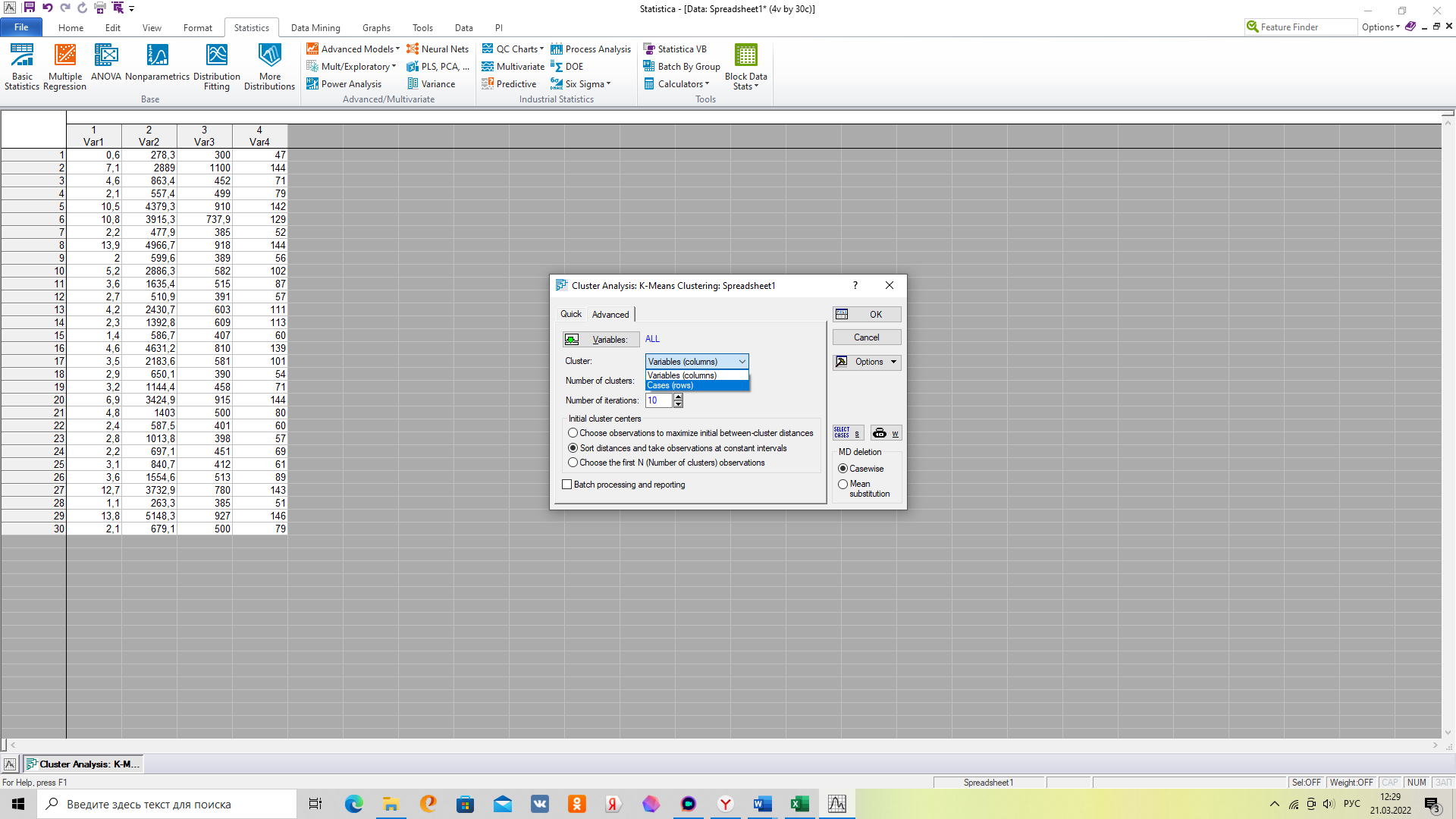
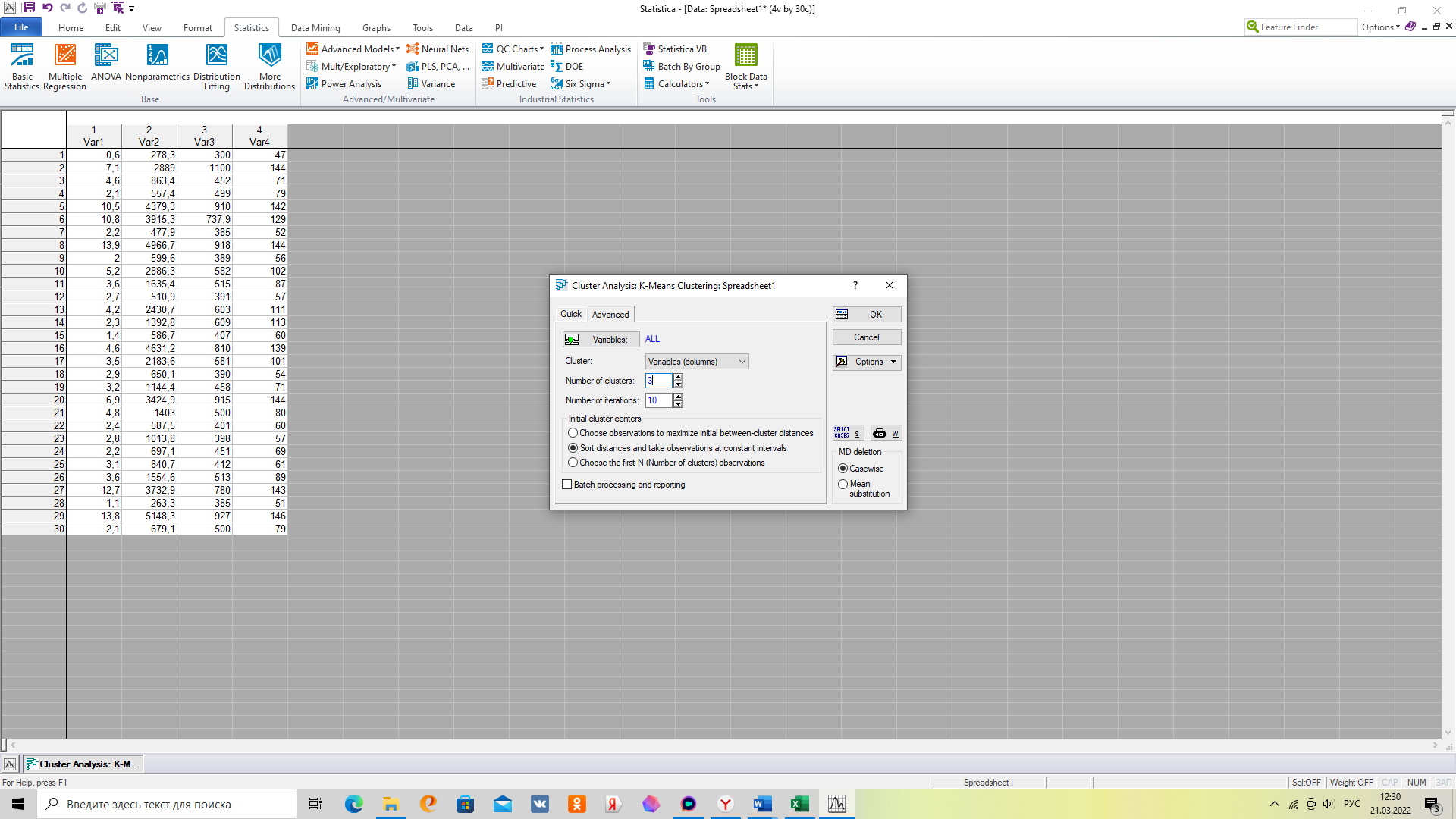
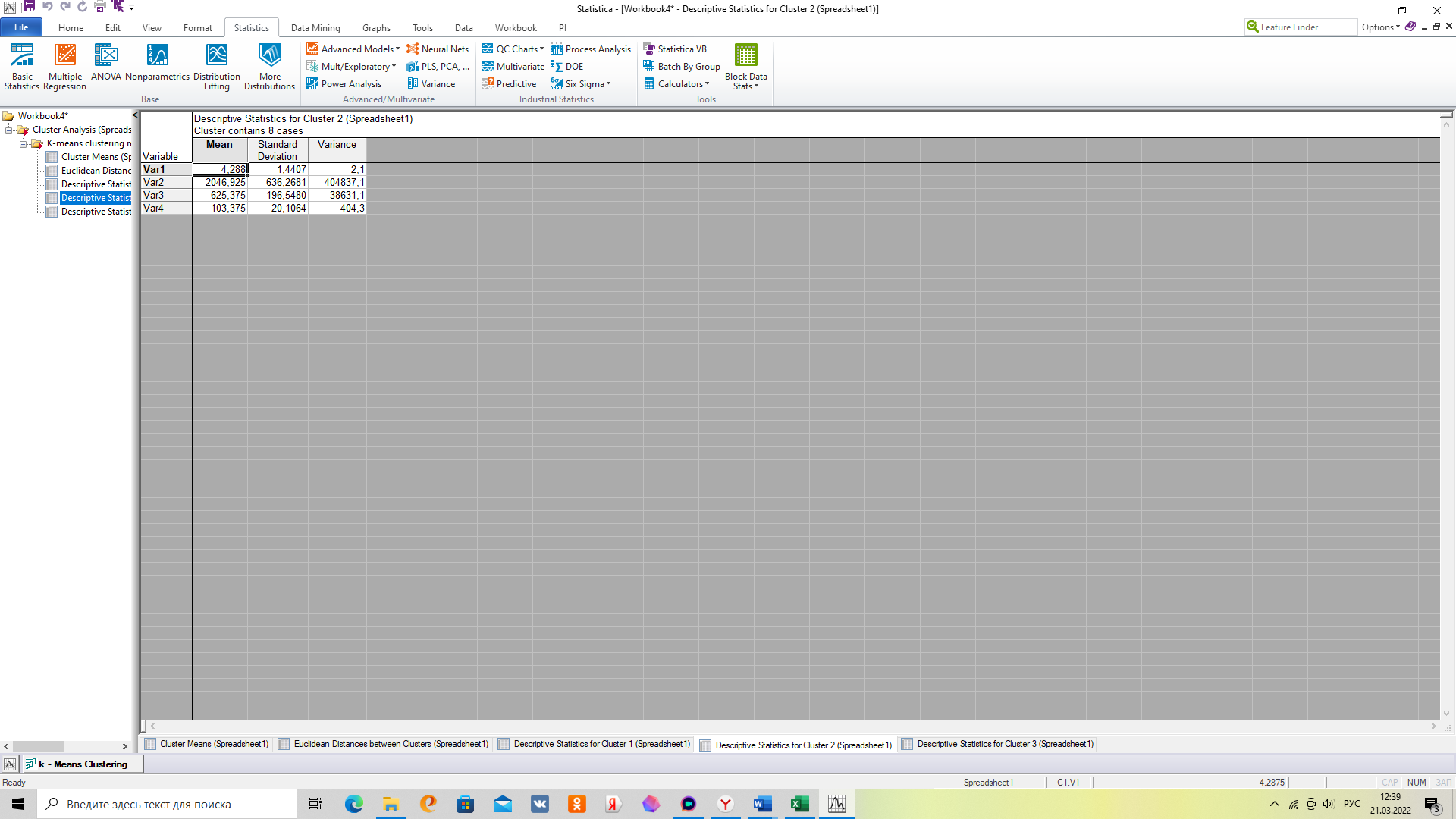
5. Для выгрузки показателей по кластерам выберете вкладку «Descriptive Statistics», после чего откроются вкладки для каждого из 3х кластеров.

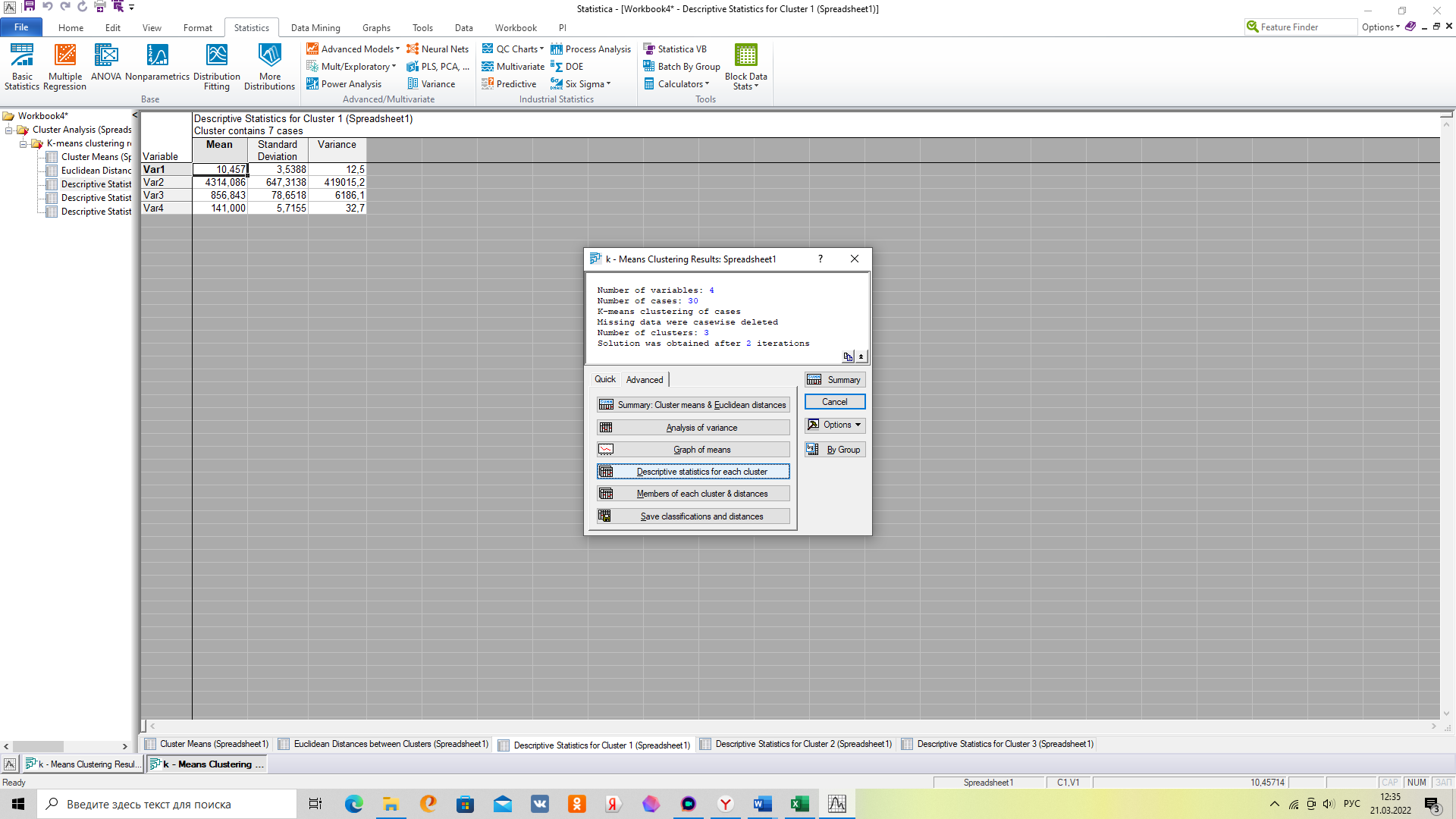
Результаты выгрузки содержат следующую информацию
Количество предприятий в кластере
Средняя
Коэффициент вариации
Стандартное отклонение
В заключение метода 1 надо установить состав кластеров и равномерность распределения.
При кластеризации методом к-средних сформировать следующие таблицы и оформить по ним выводы:
Таблица 11 – Средние по кластерам
| Показатель | Cluster - No. 1 | Cluster - No. 2 | Cluster - No. 3 |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
По показателям таблицы 2 сделать вывод о значимости показателей для кластера. Для построения таблицы 2 воспользуйтесь следующей вкладкой
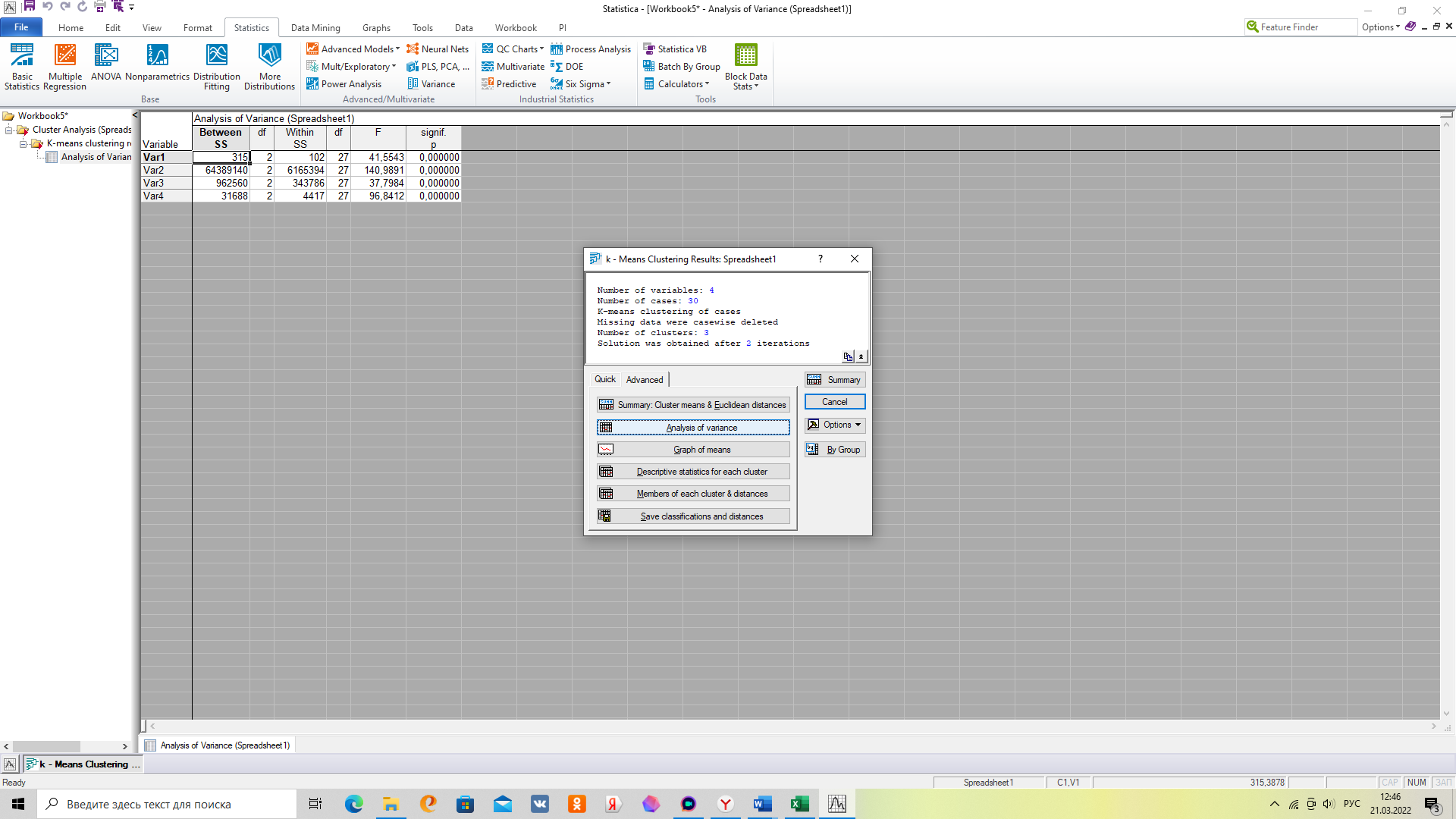
Таблица 2– Дисперсионный анализ кластеров
| Variable | Analysis of Variance (Spreadsheet1) | ||||||||||
|
|
|
|
|
| ||||||
| 315 | 2 | 102 | 27 | 41,5543 | 0,000000 | |||||
| 64389140 | 2 | 6165394 | 27 | 140,9891 | 0,000000 | |||||
| 962560 | 2 | 343786 | 27 | 37,7984 | 0,000000 | |||||
| 31688 | 2 | 4417 | 27 | 96,8412 | 0,000000 | |||||
Значимость параметров оценивается по последнему столбцу (должен быть менее 0,05).
Оформите выводы о составе и показателях кластеров.
Кластерный анализ методом к-средних (в старых версиях пакета)
-
Statistics - статистика -
Mult/ Exploratory-многомерный разведочный анализ -
Cluster – кластерный анализ -
K-means clustering- метод К-средних -
Cases rows – наблюдения строки -
Variables – обозначить переменные для анализа -
Advanced – дополнительно:
Number of cluster – число кластеров ( возьмите 3) или ориентируйтесь на результаты иерархического кластерного анализа;
Number of iterations-10-15
-
Advanced -
Analysis of variance – дисперсионный анализ, по величине F критерия судим какой признак наибольшим образом повлиял на различия между кластерами -
Members of each cluster- номера наблюдений входящих в каждый кластер. Внизу этой таблицы обозначены номера кластеров. -
Craph of means- график средних
Сопоставьте разбиение регионов по группам с проведенным результатом рейтингования по многомерной средней (в частности, посмотрите, в какой кластер попали регионы – лидера рейтинга, а также регионы – аусайдеры рейтинга).