ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ


МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

МЕХАНИКА

ОТЧЁТ

По виртуальной лабораторной работе №18
По дисциплине: Физика



Выполнил: студент гр. ТПП-21 /Кушнер М.Д./

(группа) (подпись) (Ф.И.О.)

Дата:
Проверил: _______________ / /

(должность) (подпись) (Ф.И.О.)

Санкт-Петербург

2022

Цель работы

Определить коэффициент теплопроводности твердого тела методом сравнения с теплопроводностью эталонного образца из известного материала.

Явление, изучаемое в работе: теплопроводность металлов.

Краткое теоретическое содержание

1. 
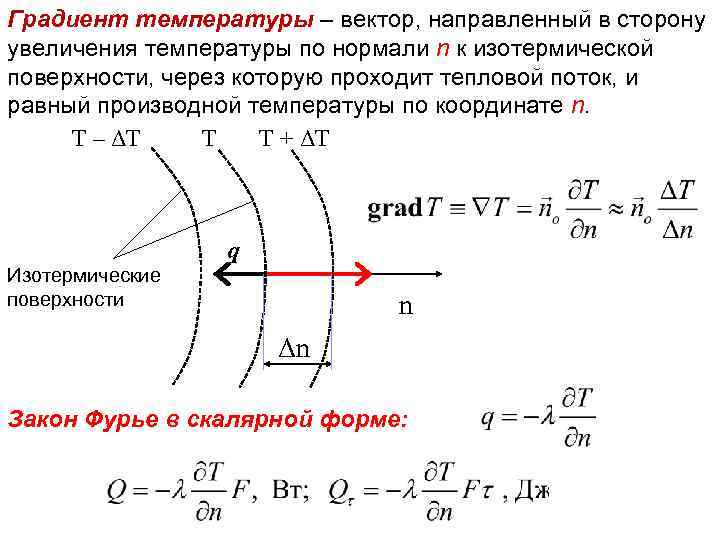
   Коэффициент теплопроводности - физическая величина, характеризующая и численно равная плотности потока энергии при градиенте температуры равной единице.
   
2. 
   Тепловой поток – количество теплоты, проходящее в единицу времени через произвольную поверхность (Вт).
   
3. 
   Плотность теплового потока – количество тепла, проходящее в единицу времени через единицу площади поверхности (Вт/м2).
   
4. 
   Теплопроводность – молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры.
   
5. 
   Коэффициент теплопроводности характеризует способность вещества проводить тепло. Численно эта характеристика равна количеству теплоты, проходящей через образец материала толщиной в единицу длины (1м), площадью в единицу площади (1м²), за единицу времени (1 секунду) при единичном температурном градиенте (1К).
   
6. 
   Закон Фурье устанавливает величину теплового потока при переносе тепла посредством теплопроводности. Согласно основному закону теплопроводности — закону Фурье (1822 г.), вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален градиенту температуры: q = — λ grad t, (3) где λ — коэффициент теплопроводности вещества; его единица измерения Вт/ (м·К). Знак минус в уравнении (3) указывает на то, что вектор q направлен противоположно вектору grad t, т.е. в сторону наибольшего уменьшения температуры.
   
7. 
   Законы. В плоской стенке распределение температуры подчиняется линейному закону и зависит от толщины стенки b и от значения температуры на её поверхностях t1 и t2. Тепловой поток, преодолевая толщу металла и не успевая перейти в охлаждающую среду, вызывает повышение температуры непосредственно CPU.
   
8. 
   Способ определения теплопроводности твердых тел, включающий пропускание равномерного теплового потока через исследуемый образец, измерение перепада температуры на образце, скорости изменения температуры при постоянной мощности нагрева, отличающийся тем, что потери тепла учитывают за счет поправочного коэффициента, который определяют по измерениям на эталонных образцах, размеры исследуемого и эталонных образцов одинаковые, теплопроводность определяют по формуле:
   

---

λ=(k⋅2W+Cx⋅b)⋅h/(2S⋅(T1-T2)),

где k - поправочный коэффициент; W - мощность электронагревателя; Сх - теплоемкость теплоприемника; b - скорость изменения температуры образца; h - толщина образца; S - площадь поперечного сечения образца; (T1-T2) - перепад температуры на образце.

9. 
   Тепловые процессы или теплообмен -- обобщенное название процессов передачи энергии в виде теплоты между телами, имеющими различную температуру. Движущей силой процесса теплообмена является разность температур. Причем передача теплоты осуществляется от тела с большей к телу с меньшей температурой.
   

К тепловым процессам, используемым в промышленности, относятся процессы нагревания, охлаждения, испарения и конденсации.

10. 
    
    

Если в термодинамической системе нарушить равновесие, например, нагреть одну из поверхностей пластины из теплопроводящего материала, то возникают необратимые (с точки зрения термодинамики) процессы. После прекращения внешнего воздействия возникает процесс релаксации, в результате которого система вновь приходит в равновесное состояние. Но в случае, когда воздействие извне постоянно, неравновесное состояние сохраняется во времени, а возникшие процессы будут стационарны, т. е не зависящими от времени.

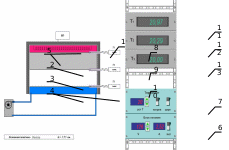
Схема установки:

Рис.1

1. 
   Нагреватель
   
2. 
   Пластина из материала с известным коэффициентом
   
3. 
   Пластина из материала с исследуемым коэффициентом
   
4. 
   Холодильник
   
5. 
   Обкладки
   
6. 
   Блок питания
   
7. 
   Термостат
   
8. 
   Термопара №1
   
9. 
   Термопара №2
   
10. 
    Термопара №3
    
11. 
    Табло температур №1
    
12. 
    Табло температур №2
    
13. 
    Табло температур №3
    

Основные расчетные формулы

1. 
   Элементарный поток тепла δQ,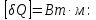
   

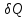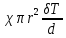= , где

d-толщина однородной пластинки,

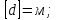
S-площадь поверхности пластинки

---

, ;

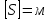δT-разность температур,

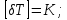
- коэффициент теплопроводности, характеризующий свойства среды,

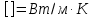
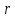– радиус пластинки,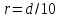

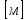
Значение коэффициента теплопроводности  может быть определено непосредственно из формулы (1), однако точное определение потока тепла δQ практически невозможно, поэтому в настоящей работе производится сравнение коэффициента теплопроводности исследуемого материала ₁ с коэффициентом теплопроводности некоторого другого материала с известным значением коэффициента теплопроводности ₂, принятого за эталон. При этом можно избежать измерения потока тепла.

2. 
   Коэффициент теплопроводности исследуемой пластины _2, :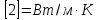
   

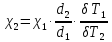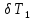, где и 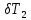- перепады температур на пластинках,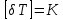

3. 
   Перепад температур на пластинках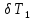 и ,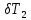
   

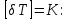
dT₁ = (T₁ - T₂) - перепад температур на эталонной пластине,

dT₂ = (T₂- T₃) -перепад температур на исследуемой пластине

Где 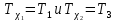- температуры эталонной и исследуемой пластинок соответственно

Основные формулы расчета погрешности

1. 
   Среднее значение величины:
   

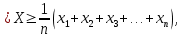где n – количество измерений

2. 
   Средняя абсолютная погрешность косвенного измерения коэффициента
   

---

теплопроводности,



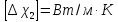
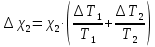
Погрешности прямых измерений

;

;

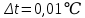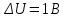Исходные данные

Эталонный образец: алюминий

Исследуемый образец: медь

d_{1(эталонная)} = 0,006 м

d_{2(исследуемая)} = 0,005 м

t_x = 20 ⁰C

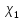= 203,5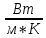

Таблица измерений и вычислений

Физическая величина	U	T1	T2	T3	dT1	dT2	2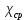
Единица измерения № Опыта	В	°С	°С	°С	К	К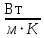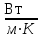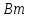
1	25	20,02	20,01	20	0,01	0,01	169,58	349,73	6,65
2	50	20,08	20,05	20	0,03	0,05	282,63		5,54
3	75	20,17	20,12	20	0,05	0,12	407,00		19,16
4	100	20,31	20,22	20	0,09	0,22	414,53		35,79
5	125	20,49	20,34	20	0,15	0,34	384,38		51,29
6	150	20,70	20,48	20	0,22	0,48	370,00		69,70
7	175	20,95	20,66	20	0,29	0,66	385,94		99,97
8	200	21,24	20,86	20	0,38	0,86	383,79		129,54

---

Примеры вычислений

1. 
   Коэффициент теплопроводности исследуемой пластины _2,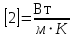
   

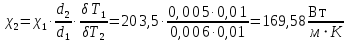
2. 
   Среднее значение коэффициента теплопроводности пластины
   

3. 
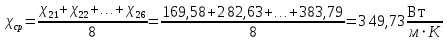
   Элементарный поток тепла δQ,
   

4. 
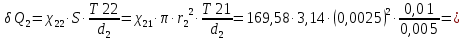
   Перепад температур на эталонной пластине
   

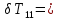(T₁₁ - T₂₁) = 20,02 - 20,00 = 0,02 K

5. 
   Перепад температур на исследуемой пластине
   

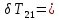(T₂₁ – T₃₁) = 20,01 - 20,00 = 0,01 K

Таблица данных для графика:



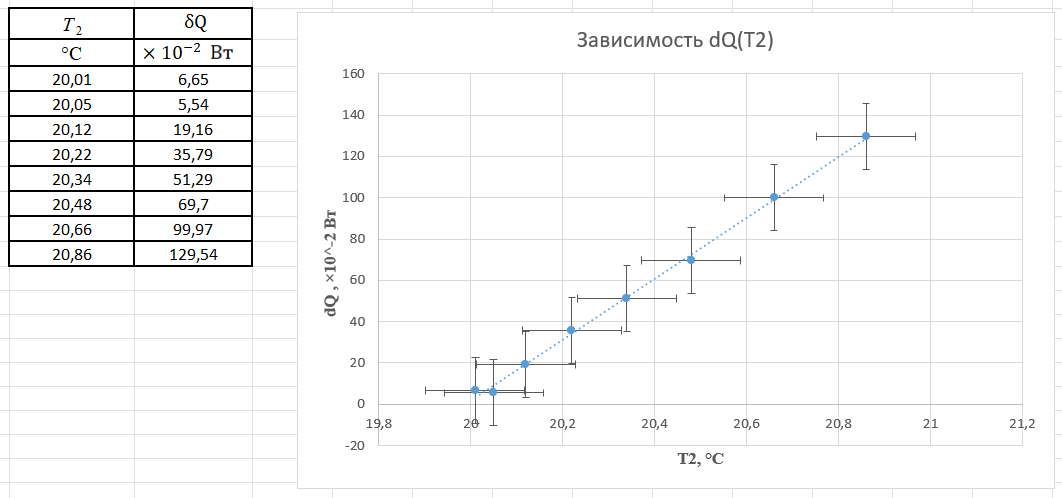
График 1. Зависимость значения отношения изменения потока тепла и температуры поверхности исследуемой пластины (T₂)

Из данного графика видно, что поток тепла, излучаемый пластинкой, возрастает по мере повышения температуры.

Расчет погрешностей

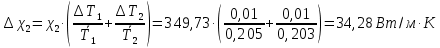
Экспериментальные данные	Справочные данные
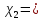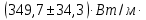K	384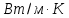

Сравнение с табличным значением:

Коэффициент теплопроводности меди = 384

Косвенных измерений

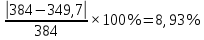
Вывод

В ходе лабораторной работы был определен материал исследуемой пластины – Медь, коэффициент теплопроводности меди 349,73

---

Смотрите также файлы

• Урок 3 Тема. Строение растительной клетки. Цель урока Изучить строение растительной клетки. Задачи урока.docx

• Семинарскопрактическое занятие 5 по темам Ощущение и восприятие.docx

• Финансовый учет и отчетность пробный экзамен июнь 2022 правила для экзамена 21 июня 2022.pdf

• Кафедра природообустройства, водопользования и охраны водных ресурсов.docx

• Изм. Лист докум. Подп. Дата Разраб.pdf