Метод Эйлера для решения задачи Коши в Excel -2010

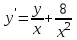
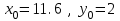
Пример: Методом Эйлера решить задачу Коши для обыкновенного дифференциального уравнения первого порядкаВзять шаг h=0,2. Сделать четыре шага.Результатом численного решения дифференциального уравнения является таблица вида

				…
				…

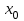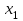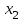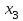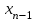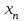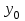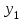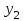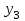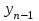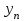Метод Эйлера заключается в вычислении нескольких значений функции 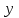по формуле: 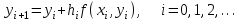.Здесь 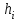– шаг, который может быть как переменным, так и постоянным, 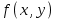– правая часть дифференциального уравнения. В нашем за­дании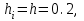

---

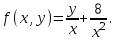
Составим таблицуЗ 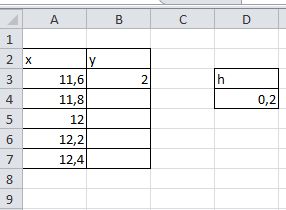десь в ячейки А12 и В12 введены значения , в ячейку D4 – значение шага (0,2). Поскольку надо сделать 4 шага, то есть вычислить 4 значения y, то х₁=11,8 , х₂=12, х₃=12,2, х₄=12,4. Эти значения введены в ячейки А4-А8. В ячейку В4 вводим формулу (см. таблицу )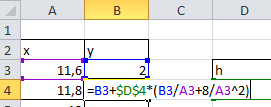Адрес ячейки, где находится h – абсолютный. 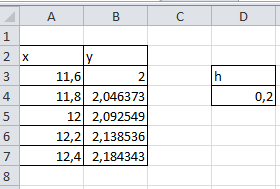В скобках записано значение правой части дифуравнения при .Поставив курсор в правый нижний угол ячейки В4 и протянув его вниз, получим искомое решение:Нанесем полученные точки на график. 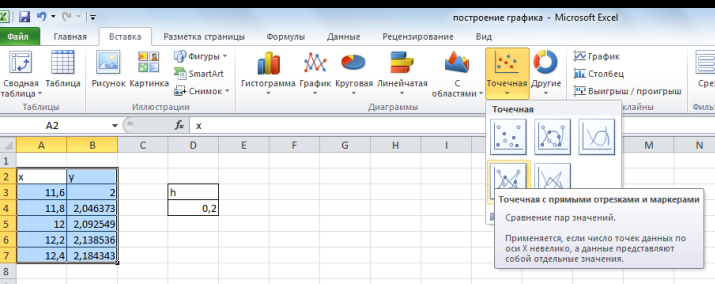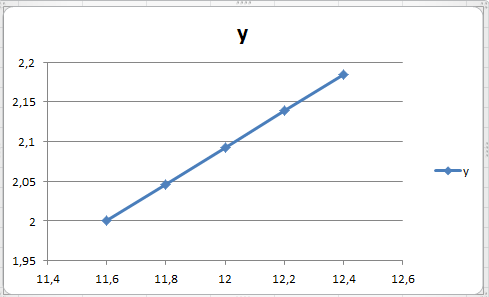Для этого выделяем таблицу (вместе с заголовками), выполняем пункт меню Вставка – Точечная – Точечная с прямыми отрезками и маркерами.Получаем:Полученный график можно отредактировать.

---

Смотрите также файлы

• Практических заданий по дисциплине общая профессиональная риторика в рекламной и паблик рилейшнз деятельности.docx

• 2 Детское общество как фактор социализации.docx

• Анализ результатов промежуточной аттестации в форме комплексной контрольной работы. Класс 1 А.docx

• Правовая охрана редких исчезающих видов растений и животных.docx

• 10. 04. 2012 1 Гипертоническая болезнь.pdf