ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

Факультет «Институт непрерывного образования (ИНО)»

Направление 11.03.02 - Инфокоммуникационные технологии и системы связи


Контрольная работа:

по дисциплине

«Метрология, стандартизация и сертификация»
Вариант 7

Выполнил: студент группы

Студенческий билет: №

Санкт-Петербург

2021 г


Задача 1. ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
С помощью моста проведен ряд независимых измерений сопротивления образцового резистора R0 = 1300 Ом.

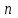	1	2	3	4	5
R, Ом	1341	1336	1355	1329	1331

Предполагая, что случайная погрешность имеет нормальный закон распределения, определить:

1. 
   среднюю квадратическую погрешность однократного измерения;
   
2. 
   результат измерения затухания и его среднюю квадратическую погрешность;
   
3. 
   доверительный интервал погрешности результата измерения при доверительной вероятности 0,9;
   
4. 
   систематическую погрешность определения затухания;
   

Можно ли считать доказанным наличие систематического отклонения затухания от номинального значения?

Решение:

1. Определим среднее значение измеряемой величины и среднеквадратичное отклонение.

Среднее арифметическое значение измеряемой величины:



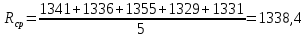
Среднеквадратичное отклонение погрешности результата наблюдений (стандартной неопределенности единичного измерения):

---

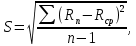
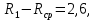
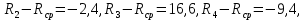
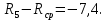
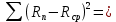431,2, 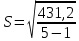=10,38.

2. Результат измерения затухания и его среднюю квадратическую погрешность;

За результат измерения принимается среднее арифметическое ряда наблюдений R_ср = 1338,4.

Определим среднюю квадратическую погрешность результата измерения:

Согласно формуле ([1] 4.30)



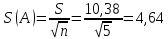
3. Доверительный интервал погрешности результата измерения при доверительной вероятности 0,9;

Границы доверительного интервала погрешности



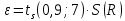
Здесь t_S(0,9;5) — коэффициент Стьюдента для 5 измерений при доверительной вероятности Р = 0,9. В нашем случае t_S(0,9;5) = 2,132. Тогда



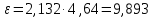
Оставим в погрешности результата 2 значащие цифры.

Результат измерения в соответствии с правилами представления результата запишем следующим образом:
R = (1338,4 ± 9,89) Ом; Р_R = 0,9; n = 5

4. Систематическая погрешность определения затухания.

ΔR = 1338,4 – 1300 = 38,4 Ом

Рассмотрим интервал значений, принимаемых измеряемой величиной.

1338,4-9,89 ≤ R 1338,4+9,89

1328,51 ≤ R ≤ 1348,29

Так как истинное значение сопротивления R0=1300 Ом не попадает в этот интервал, при допущении о нормальном законе распределения случайной величины можно сделать вывод, что прибор имеет систематическую погрешность.
Задача 2. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ

Определите показания вольтметров всех возможных модификаций при

измерении напряжения, форма которого показана на рис.1


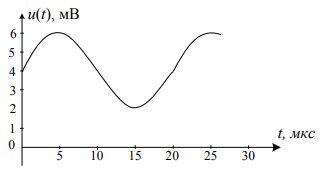
Рисунок – 1
Решение:

Запишем аналитическое выражение сигнала в пределах одного периода.

????(????) = 4 + 2 ∙ sin(????????)

Амплитуда сигнала:

???????? = 2 В

Период сигнала: Т = 20 мкс

Частота сигнала:

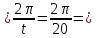???? 0,1

---

Найдем среднее значение напряжения, которое можно вычислить по

формуле:



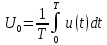
Подставляя аналитическое выражение данного сигнала, получаем:





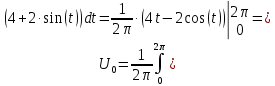
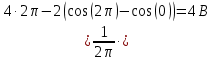
Найдем средневыпрямленное значение напряжения, которое можно

вычислить по формуле:


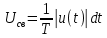
Рассматриваемый сигнал не имеет отрицательных значений

напряжения на протяжении всего периода, поэтому средневыпрямленное

значение напряжения данного сигнала совпадает сего средним значением:


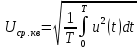
Подставляя аналитическое выражение данного сигнала, получаем:









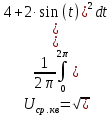
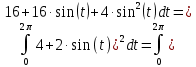
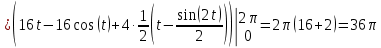
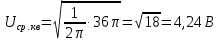
Показания вольтметров с открытым (ОВ) и закрытым входом (ЗВ)

различаются тем, что вольтметр с закрытым входом отсекает постоянную

составляющую сигнала.

Находим показание вольтметров с открытым входом.

Пиковый вольтметр с открытым входом ( )

Найдем пиковое значение: 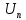= max(u(t))

В данном случае: 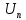= 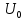+ 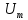= 4 + 2 = 6 В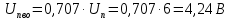


Линейный вольтметр с открытым входом ( )

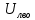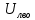= 1,11∙ 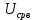= 1,11∙4 = 4,44 В

Квадратичный вольтметр с открытым входом ( )

---

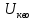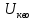
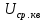= = 4,24 В
Для нахождения показаний вольтметров с закрытым входом необходимо

вычислить напряжения из предыдущего пункта за вычетом постоянной

составляющей.



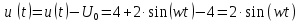
Пиковое значение: 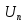= max( 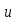(????)) = 2 В


Найдем средневыпрямленное значение напряжения без постоянной

составляющей:



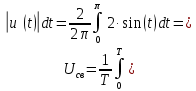
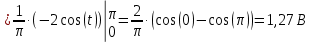
Найдем среднеквадратическое значение напряжения без постоянной

составляющей:






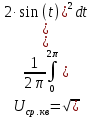
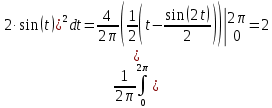
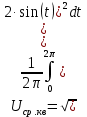
Находим показание вольтметров с закрытым входом. Пиковый вольтметр с закрытым входом ( )

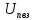=0,707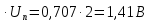

Линейный вольтметр с закрытым входом ( )

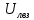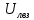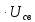=1,11 =1,11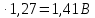

Квадратичный вольтметр с закрытым входом ( )

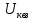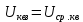=1,41 В

Задача 3. ПРИМЕНЕНИЕ ЭЛЕКТРОННО-ЛУЧЕВОГО ОСЦИЛЛОГРАФА
Для измерения частоты синусоидального сигнала методом фигур Лиссажу этот сигнал был подан на вход Y осциллографа. Для сравнения на вход Х был подан эталонный синусоидальный сигнал и после подстройки его частоты- на экране возникла неподвижная фигура, показанная на рис. 2



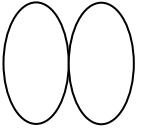
Рис. 2

Частота эталонного сигнала равна 2367 Гц, а ее относительная погрешность ±0,5%. Определите значение частоты измеряемого сигнала, оцените абсолютную погрешность измерения.

---

Решение:

Определим, сколько раз за один период луч осциллографа пересекает оси Х и Y рисунок 3.



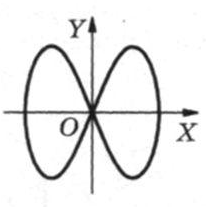
Рисунок – 3

Для расчета измеряемой частоты необходимо воспользоваться правилом Лиссажу:

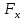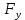* x = * y

X и У - количество пересечений фигуры Лиссажу с соответствующими осями. x=4; y=

Зная образцовую частоту 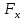, рассчитаем частоту измеряемого сигнала: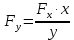



:

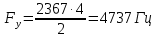Абсолютная погрешность это разница между результатом измерения 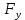и истинным значением 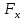измеряемой величины. Абсолютная погрешность находится как 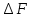= 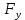- 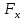и выражается в единицах измеряемой величины.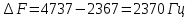



Задача 4. ЦИФРОВЫЕ ИЗМЕРЕНИЯ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ
Построить график зависимости суммарной абсолютной погрешности электронно-счетного (цифрового) частотомера в режиме измерения частоты от частоты измеряемого сигнала в диапазоне 10 Гц - 10 МГц. Напишите соответствующую формулу и назовите составляющие суммарной погрешности. Время счета, которое можно установить с помощью переключателя принять равным 0,1 с. Значение относительной погрешности опорного кварцевого генератора частотомера принять равным ±2∙10^-6. При построении использовать логарифмический масштаб по осям координат. С какой абсолютной погрешностью можно измерить таким прибором частоту сигнала 1234567,89 Гц при указанном времени счета. Записать в соответствии с правилами возможный результат измерения.

Решение:

1. Результирующая (суммарная) предельная относительная погрешность измерения частоты 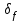определяется двумя составляющими [2, форм. 5.5].

---

Смотрите также файлы

• Социология массовых коммуникаций.docx

• Кривая спроса на труд неверный ответ работниками, максимизирующими полезностями.docx

• Описание моей собаки.docx

• Пн Алгебра 3тосан Бекітемін 1саба.docx

• Курсовая работа по дисциплине Административное право на тему Административный арест понятие, основание, механизм применения.doc