Добавлен: 08.11.2023
Просмотров: 87
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Тверь
Кафедра Биотехнологии, химии и стандартизации
КУРСОВАЯ РАБОТА
по дисциплине: «Метрология».
Выполнил:
Студент __ курса
__________ обучения
группы Б.СМ.СС. _____
______________________
ФИО
Подпись _____________
Проверил:
к.т.н., доцент кафедры
Иванова Наталья Игоревна
Оценка _____________
Дата _____________
Подпись _____________
Тверь 2023
Содержание
Задание № 1 Методы исключения результатов с грубыми погрешностями 3
Задание № 3 Обработка результатов косвенных измерений при нелинейной зависимости 10
Задание №4 Разработка рационального режима метрологического обеспечения объекта 13
Список использованных источников 23
Задание № 1 Методы исключения результатов с грубыми погрешностями
Теоретическая часть
Грубые погрешности (промахи) относятся к числу погрешностей, изменяющимся случайным образом при повторных наблюдениях. Они явно превышают по своему значению погрешности, оправданные условиями проведения эксперимента.
Причинами грубых погрешностей могут быть неконтролируемые изменения условий измерений, неисправность, ошибки оператора и др.
Для исключения грубых погрешностей применяют аппарат проверки статистических гипотез. В метрологии используются статистические гипотезы, под которыми понимают гипотезы о виде неизвестного распределения, или о параметрах известных распределений.
Примеры статистических гипотез:
1) рассматриваемая выборка (или ее отдельный результат) принадлежит генеральной совокупности;
2) генеральная совокупность распределена по нормальному закону;
3) дисперсии двух нормальных совокупностей равны между собой.
При выдвижении и принятии гипотезы могут иметь место следующие четыре случая:
1) гипотеза принимается, причем и в действительности она правильная;
2) гипотеза верна, но ошибочно отвергается. Возникающую при этом ошибку называют ошибкой первого рода, а вероятность ее появления называют уровнем значимости и обозначают q(α) ;
3) гипотеза отвергается, причем в действительности она неверна;
4) гипотеза неверна, но ошибочно принимается. Возникающую при этом ошибку называют ошибкой второго рода, а вероятность ее появления обозначают β.
Все статистические критерии являются случайными величинами, принимающими определенные значения (таблицы критических значений). Областью принятия гипотезы (областью допустимых значений) называют совокупность значения критерия, при которых гипотезу принимают. Критической называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Область принятия гипотезы и критическая область разделены критическими точками, в качестве которых и выступают табличные значения критериев.
Область непринятия гипотезы может быть односторонней (правосторонней или левосторонней) и двух сторонней.
Основной принцип проверки статистических гипотез формулируется следующим образом: если наблюдаемое (опытное) значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.
Критерий Смирнова используется при объемах выборки п > 25 или при известных значениях генеральных среднего и СКО. Он устанавливает менее жесткие границы грубой погрешности. Для реализации этого критерия вычисляются действительные значения квантилей распределения (наблюдаемое значение критерия) по формуле:
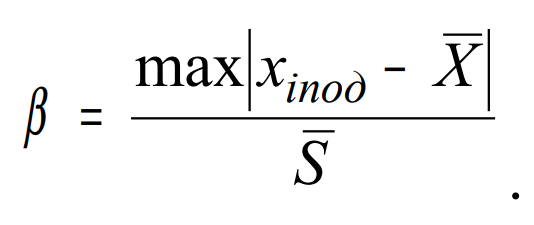
Найденное значение сравнивается с критериальным βтабл, приведенным в таблице 3.6 [1].
Практическая часть
Вариант 6. Используя критерий Смирнова, определить, не содержит ли результаты наблюдений грубые погрешности.
Результаты наблюдений
Решение
1. Вычисление среднего арифметического и СКО результатов наблюдений для всей выборки
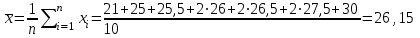
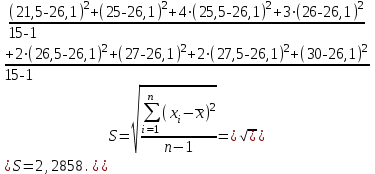 а) Наибольшая разница между средним и крайним значением:
а) Наибольшая разница между средним и крайним значением: 26,15 – 21= 5,15
Вычисляем квантиль


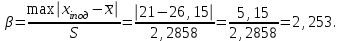
2. Определяем вероятность выхода результатов за квантиль:
В таблице 3.6 [1] для числа измерений n=10 и вероятности P=0,05 находим табличное значения коэффициента βтабл = 2,568.
β< βтабл (2,253 < 2,568), значит xi = 21 не является грубой погрешностью.
Ответ
При вероятности P=0,05 результат наблюдений не содержит грубые погрешности.
Задание № 2 Исключение систематических погрешностей измерений
Теоретическая часть
Основные способы исключения систематических погрешностей сводятся к устранению их до начала измерения, в процессе измерения, внесения поправок в результат измерения, а также оценке границ систематических погрешностей.
Устранение до начала измерения преследует цель: предварительную проверку всех приборов по эталонному образцу и проверку соединения отдельных элементов. Устранение влияния температуры, например, осуществляется различными способами термостатирования. При этом не всегда удается естественным путем сохранить температуру точно 20 0С. Тогда ее стабилизируют на уровне (30-40) 0С с использованием равномерного подогрева всего помещения или способом кондиционирования
воздуха. Затем используют поправочные коэффициенты. Устранение влияния магнитных полей проводят с помощью магнитного экранирования. Устранение вибраций проводят с помощью губчатой резины и эластичных подвесок.
Устранение в процессе измерения – это наиболее эффективный прием исключения погрешностей. Используют способ замещения, когда измеряемый объект замещают эталонной моделью, например, взвешивание на рычажных весах по способу Борда. На одну чашку весов кладут взвешиваемую массу, на другую – специальный груз (например, дробь), до уравновешивания весов. Затем взвешиваемую массу снимают и на ее место устанавливают гири до достижения равновесия. Суммарный вес гирь более точно соответствует взвешиваемой массе. Способ замещения широко используется при измерении электрических параметров сопротивления, емкости, индуктивности с использованием мостовой схемы.
Применяют также способ противопоставления, когда измерения проводят два раза таким образом, чтобы причина систематической погрешности при втором измерении была противоположна по знаку по сравнению с первым измерением. Например, второе взвешивание массы проводят на другой чашке весов. Затем определяется среднее значение результатов двух взвешиваний. Аналогично определяется сопротивление равноплечного моста.
Внесение поправок в результат измерения применяется, если в результате поверки обнаружилось, что, например, вольтметр дает заниженные показания. Тогда определяется поправочный коэффициент и результат измерения умножается на этот коэффициент. Обычно на разных
диапазонах измерения поправочные коэффициенты разные. Иногда таблицу поправочных коэффициентов завод-изготовитель прилагает к паспорту прибора.
Перечисленные выше способы устранения погрешностей не исключают полностью систематические погрешности (существует ее остаток – неисключенная систематическая погрешность). Поэтому выполняется оценка границ систематических погрешностей. Это связано с тем, что причины их возникновения самые разнообразные и не всегда правильно учитываемые. Даже если есть поправки к показанию специального лабораторного прибора, то они разные для разных диапазонов измерения не только по величине, но и по знаку.
Если действительное показание прибора при проведении эксперимента может иметь широкий диапазон, то принимают систематическую погрешность в пределах максимальной погрешности по паспорту завода – изготовителя. Постоянные систематические погрешности измерений могут быть выявлены (обнаружены) путем сравнения результатов измерений с другими, полученными более точными методами и средствами.
Постоянная составляющая систематической погрешности не может быть выявлена, ни тем более найдена методами совместной обработки результатов. Поэтому задача исключения переменной систематической погрешности может решаться как при отсутствии, так и при наличии постоянной систематической погрешности. Если во всех результатах наблюдений содержится постоянная систематическая погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.
Переменная