Файл: Кшм в паровых машинах 3 кшм в двигателях внутреннего сгорания 5.docx

F_jп^max = – m_п ² R (1 + _ш). (14.15)

Из (14.15) следует, что при прочих равных условиях, чем короче шатун l_ш и больше ход поршня S, тем больше _ш и силы инерции поступательно движущихся масс F_jп^max.

При номинальных угловых скоростях коленчатых валов современных поршневых ДВС, силы инерции поступательно движущихся масс достигают весьма больших величин и зачастую превышают силы давления газов. Например, для спортивных моторов характерны номинальные частоты вращения n_N  14000 … 17000 об/мин. При этом максимальные ускорения поршня j_п^max  100 тысяч м/с², а средние скорости поршня  35 м/с. Даже для обычного современного легкового автомобиля характерны n_N  6000 об/мин; j_п^max  20000 м/с²;  16 м/с. При m_п = 1 … 3 кг для таких двигателей F_jп^max измеряются десятками килоньютонов.

В соответствии с классической методикой динамического расчёта КШМ определяют суммарную силу от газовых и инерционных сил поступательно движущихся масс, хотя последние приложены в различных местах. Так газовые силы являются поверхностными, то есть воздействуют только на днище поршня, а силы инерции являются объёмными и воздействуют на каждую частицу движущихся тел

F_ = F_г + F_jп. (14.16)

Характерные графики изменения сил давления F_г , сил инерции поступательно движущихся масс F_jп и их суммарной силы F_ отражены на рис. 14.5, где нетрудно заметить, что для 4-тактного двигателя частота изменения суммарной силы F_ в полтора раза больше частоты изменения силы инерции F_jп и в три раза больше частоты силы давления газов F_г . Для 2-тактного ДВС частота F_ в 2,5 раза больше частот изменения F_jп и F_г .

К роме сил инерции поступательно движущихся масс в КШМ имеют место силы инерции вращающихся масс – это кривошип коленчатого вала с нижней головкой шатуна и подшипником. Также имеют место силы инерции масс, совершающих сложное движение – это стержень шатуна.

Силы инерции вращающихся масс (центробежные силы) определяют

---

F_ц = m_в r ², (14.17)

где m_в – неуравновешенная противовесами вращающаяся масса;

r – расстояние от оси вращения до центра неуравновешенной вращающейся массы.

Стержень шатуна совершает сложное движение, которое с помощью метода декомпозиции можно разложить на два простых – поступательное и вращательное. Тогда сила инерции стержня шатуна F_jS включает два слагаемых – от его поступательного движения F_jSx , от вращения F_jS

F_jS = F_jSx + F_jS = – (m_S x_п’’ + J_S ’’ / l_ш), (14.18)

где m_S, J_S – масса стержня шатуна и момент его инерции относительно оси верхней головки;

’’ – угловое ускорение шатуна.

Обычно в теории ДВС сложное движение стержня шатуна не рассматривается. При этом половину массы стержня (от 1/4 до 1/3 массы всего шатуна) приводят к m_п и считают поступательно движущейся массой. Другую часть массы шатуна приводят к m_в и считают вращающейся.

О 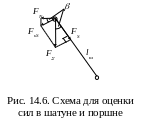севую силу, сжимающую или растягивающую шатун F_S, и боковую силу F_N , с которой поршень воздействует на цилиндр, следует определять согласно схеме, приведенной на рис. 14.6.

F_S = ; (14.19)

F_N = . (14.20)

Нетрудно заметить, что при разложении силы F_ , как показано на рис. 14.6, появляется составляющая F_кS , направленная перпендикулярно к оси шатуна, то есть поворачивающая его относительно оси нижней головки.

Силы, нагружающие коленчатый вал, вычисляют с помощью осевой силы шатуна F_S и сил инерции вращающихся масс F_ц. Для этого используют динамическую модель, изображённую на рис. 14.7.

О севая сила кривошипа 

---

F_к нагружает коренные подшипники коленчатого вала и определяется

F_к = F_S cos( + ). (14.21)

Окружная сила кривошипа вычисляется по зависимости

F_т = F_S sin( + ). (14.22)

В формуле для оценки центробежных сил кривошипа F_ц под m_в понимается сумма масс шатунной шейки с подшипником, нижней головки шатуна и щёк коленчатого вала. При игнорировании (14.18) к m_в также относят половину массы стержня шатуна (от 3/4 до 2/3 массы всего шатуна). Однако F_ц, действующая на коренные опоры компенсируется такими же силами от противовесов F_пр, но направленными противоположно от F_ц (см рис. 14.8), то есть должно выполняться условие F_пр = – F_ц .

С 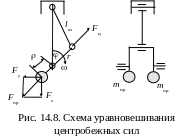уммарная центробежная сила противовесов

F_пр = 2 m_пр  ² = –m_в r ², (14.23)

где  - расстояние от оси вращения коленчатого вала до центра масс противовесов;

r – расстояние от оси вращения коленчатого вала до центра неуравновешенных масс кривошипа (обычно это расстояние принимают равным радиусу кривошипа R).

Тогда необходимую массу одного противовеса можно оценить по зависимости

. (14.24)

Для более точной оценки нагруженности коренного подшипника коленчатого вала необходимо рассмотреть две щеки с обоих его сторон, то есть осуществить геометрическое суммирование сил  , действующих в щёках соседних кривошипов. Очевидно, что угол между складываемыми векторами сил F_кi и F_кi+1 будет равен углу между смежными кривошипами, но модули указанных сил существенно различны, так как в одном цилиндре будет рабочий ход, а в другом, например, сжатие.

После оценки функций F_к = f () и F_S = f () определяются наименее нагруженные места (по углу ПКВ) шатунных и коренных шеек коленчатого вала

---

, где могут быть выполнены отверстия для подвода смазки, а также места наибольшего износа, где указанные силы максимальны.

Для правильной оценки нагрузок в КШМ и КПД двигателя необходим учёт сил трения в каждой трущейся паре, что в “классической” теории ДВС осуществляется на основе приближённых эмпирических зависимостей, например, (13.32) для потерь среднего индикаторного давления цикла p_i.

Сила трения поршня о стенку цилиндра направлена вдоль его оси

F_тр.п = – sin(v_п) f _п(F_N + F_N ст ), (14.25)

где sign(v_п) – функция знака скорости поршня;

f _п – коэффициент трения поршня о стенку цилиндра;

F_N ст – статическая сила, прижимающая поршневые кольца к цилиндру.

Силу трения в верхней головке шатуна F_тр.ш.п , которая направлена перпендикулярно силе F_, то есть прижимает шатун к пальцу, определяем по аналогии с предыдущим выражением

F_тр.ш.п = – sin(’) f _ш.п F_, (14.26)

где sign(’ ) – функция знака угловой скорости качания шатуна;

f _ш.п – коэффициент трения в паре “поршневой палец – втулка верхней головки шатуна”.

Сила F_тр.ш.п действует по той же оси, что и сила F_N .

Аналогично рассмотренным силы трения в шатунном F_тр.к.ш и коренных F_тр.к.к подшипниках коленчатого вала направлены перпендикулярно действующим в парах трения силам давления против векторов относительных скоростей движения. Их определяют по зависимостям:

F_тр.к.ш = – sin( – ’) f _к.ш F_S ; (14.27)

F_тр.к.к = – sign() f _к.к F_кk_м, (14.28)

где f _к.ш , f _к.к – коэффициенты трения в шатунном и коренных подшипниках коленчатого вала;

k_м – коэффициент учёта потерь энергии на привод механизмов и систем двигателя (кроме КШМ).

Под влиянием центробежной силы нижней головки шатуна F_ц.S в шатунном подшипнике коленчатого вала выделяем ещё одну составляющую сил трения F_тр.ц.S

F_тр.ц.S = – sign() f _к.ш.ц F_ц.S , (14.29)

где f _к.ш.ц – коэффициент трения в шатунном подшипнике коленчатого вала от действия центробежной силы шатуна F_ц.S , определяемой по (14.17), но учитывающей только массу шатуна.

---

Схему сил в КШМ можно представить как на рис. 14.9.

И 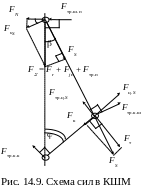з-за малости можно не учитывать силы аэродинамического сопротивления, которые преодолевает движущийся поршень, определяемые по формуле И. Ньютона F_W = – _W _к v_п² A_п , где  _W – коэффициент аэродинамического сопротивления поршня (_W  5); _к – плотность среды в картере (_к 1,2).

Коэффициент f в каждой паре трения является переменной величиной и в общем случае изменяется в довольно широких пределах (от f_max = 0,15 до f_min = 0,01). Поэтому, согласно основных положений Триботехники (наука о трении), коэффициент трения следует определять с помощью кривой Герси-Штрибека (рис. 14.10) по критерию Зоммерфельда

Z  =   , (14.30)

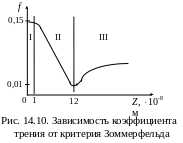где  - динамический коэффициент вязкости смазки в подшипнике скольжения;

v – скорость скольжения одной детали относительно другой;

A – площадь пары трения;

F – сила, сжимающая трущиеся детали.

При анализе кривой Герси – Штрибека выделяют три её участка (на рис. 14.10 отмечены римскими цифрами). Участок I соответствует граничному трению, то есть работе пары трения с очень большими давлениями, малыми скоростями скольжения и вязкостью смазки. Участок II соответствует смешанному трению, то есть средним давлениям, скоростям и вязкости. Участок III – чистому жидкостному трению, когда трущиеся детали полностью разделены масляной плёнкой.

В качестве аналитической аппроксимации кривой Герси – Штрибека для определения коэффициента трения можно использовать следующие регрессионные зависимости:

f  = f_ст при Z < 10^-8 м;

f = f_ст – k₁ Z при 10^-8 < Z < 1210^-8 м; (14.31)

f = k₂ + k₃ Z² при Z > 1210^-8 м,

где f_ст – статический коэффициент трения для данных материалов пары трения;

---