Задача 1.

Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, конденсатор или индуктивность. В момент времени t = 0 происходит переключение ключа К, в результате чего в цепи возникает переходной процесс.1. Перерисуйте схему цепи (таблица 2) для Вашего варианта - последним двум цифрам пароля (таблица 1).2. Выпишите числовые данные для Вашего варианта (таблица 3).3. Рассчитайте все токи и напряжение на С или L в три момента времени t: 0_-, 0₊, ∞4. 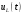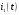Рассчитайте классическим методом переходный процесс в виде  , , 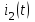  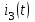в схемах 1 – 5,  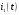, , 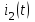,  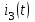  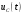в схемах 6 – 10. Проверьте правильность расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов в п. 3.5. Постройте графики переходных токов и напряжения, рассчитанных в п. 4. Определите длительность переходного процесса, соответствующую переходу цепи в установившееся состояние с погрешностью 5%.6. Рассчитайте ток 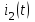 операторным методом.Решение.1.1. 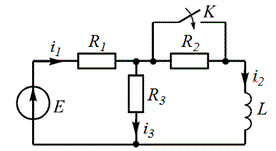Схема цепи Рис. 1.1 – схема №41.2. Параметры электрической цепи:Таблица 3.

№ вар	L, мГн	R1,кОм	R2,кОм	R3,кОм	E,В
23	10	1	2	2	12

---

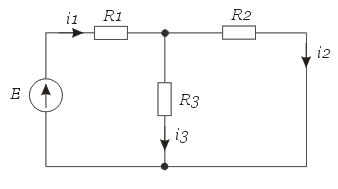
1.3. Момент времениt=0-. Ключ разомкнут.Рис. 1.2 мА мА мА
В
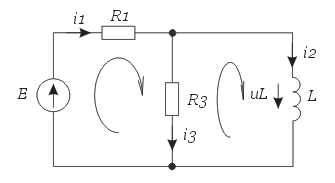
Момент времениt=0+ (или t=0). Ключ замкнут.Рис. 1.3По закону коммутации.
мА
Составляем систему уравнений по законам Кирхгофа для моментаt=0+. Решаем систему с учетом закона коммутации, находим значения в момент t=0. Находим.
мА

мА

В

---

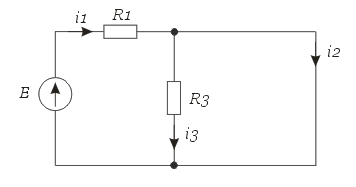
Принужденный режим. Момент времени t=∞. Ключ замкнут и шунтирует сопротивление R₂. Означает новое стационарное состояние цепи после окончания переходного процесса.Рис. 1.4
мА

мА

В
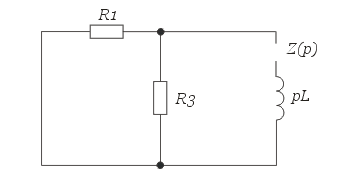
2.1. Характеристическое уравнение для расчета р составляется по операторной схеме замещения, отражающей работу цепи после коммутации.Рис. 1.5 Находим корень. Постоянная времени цепи.
с
2.2. Расчет токов и напряжения u_L(t).
мА

мА

мА

В
2.3. Проверка с пунктом 1.3.
мА

мА

---

мА

мА

мА

мА

В

В
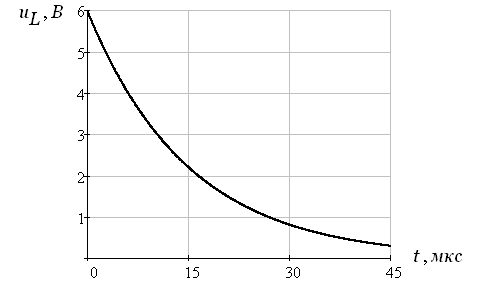
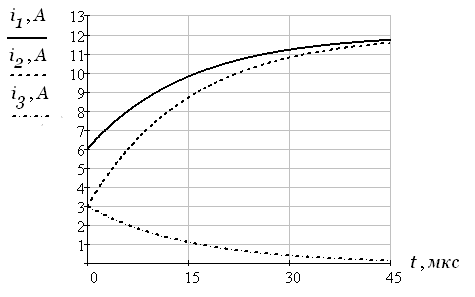
Полученные значения совпадают с результатами пункта 1.3.3. Построение графиков переходного процесса на интервале [0,3ּτ].Рис. 1.6 – напряжение на индуктивностиРис. 1.7- токи в ветвях цепи4. Расчет тока i₂(t) операторным методом.Составим операторную расчетную схему с учетом независимого начального условия.
мА
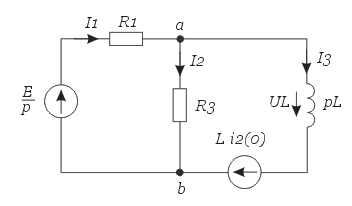
Рис. 1.8 – операторная схема замещенияИспользуя закон Ома, в операторной форме, запишем Где, После подстановок находим операторный ток I₂(p).

---

Находим оригинал по теореме разложения.
мА
Сравниваем с решением, полученным классическим способом. Результаты совпали.

Задача 2

Задача посвящена временному и частотному (спектральному) методам расчета реакции цепей на сигналы произвольной формы. В качестве такого сигнала используется импульс прямоугольной формы (видеоимпульс).Электрические схемы цепей (см. рисунок) содержат емкости С или индуктивности L, а также сопротивления R. Для всех вариантов . В схемах, где имеется сопротивление , его величина . 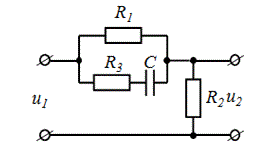Во всех схемах входным напряжением является прямоугольный импульс длительностью и амплитудой .Решение.Схема цепи.Рис. 2.1- схема №4Параметры электрической цепи:Таблица 4.

№ вар	C, пФ	R1,кОм	R2,кОм	R3,кОм	tu,нс	U1,В
23	30	1	3	0.2	40	5

---

Смотрите также файлы

• Практикум по теме 4 Заполните таблицу. Права и свободы человека в Российской Федерации.docx

• Норматив 4 Пополнение боеприпасов в ходе боя.docx

• По мнению великого античного мудрецафилософа Сократа, когда душа тугонатуго связана в теле и прилеплена к нему, то сущее само по себе человек познать не может. Почему.docx

• "Предпринимательская деятельность".rtf

• Решение Вес чмэ3 123т 1 Определение сопротивлению локомотива в режиме тяги по бесстыковому пути определяем по формуле.docx