ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 53
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 8
1. Однородный стержень длины l имеет теплоизолированную боковую поверхность. Известно распределение температуры в начальный момент времени
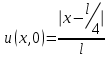, а также температура, поддерживаемая на краях стержня 
, 
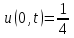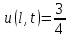. Используя метод Фурье, найти распределение температуры стержня в произвольный момент времени.Решение
Поставим начально краевую задачу:
, 
, 
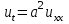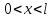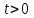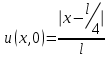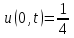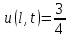, , , .Для применения метода Фурье получим однородные граничные условия. Будем искать решение задачи в виде
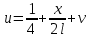, где функция v удовлетворяет однородным граничным условиям. Получим для нее уравнение и начальное условие:
.
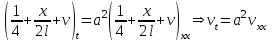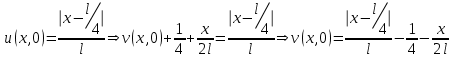.Поскольку
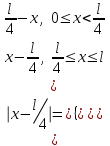, тогда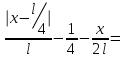 
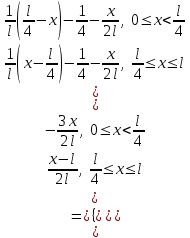
Получили вспомогательную задачу:
, , ,
, 
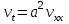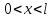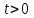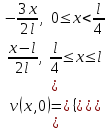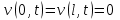.Будем искать решение задачи в виде
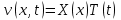, тогда уравнение примет вид:
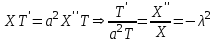.Из тождества получаем систему уравнений:
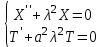
Получим граничные условия для первого уравнения системы:
,
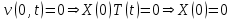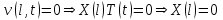.Для первого уравнения системы получаем задачу Штурма-Лиувилля:
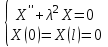
Нетривиальное решение уравнения при
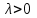имеет вид:
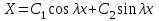,Из граничных условий получаем:
,
,
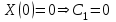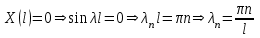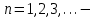собственные значения задачи, тогда 
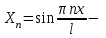собственные функции задачи (с точностью до константы).Решение второго уравнения с учетом собственных чисел
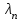имеет вид:
, 
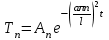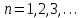
В силу линейности и однородности уравнения решение задачи имеет вид:
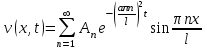.Найдем коэффициенты ряда из начального условия:
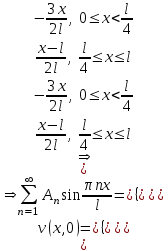
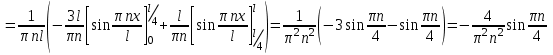.Таким образом, решение задачи имеет вид:
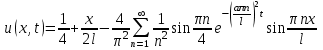.Ответ:
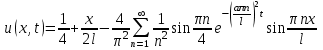.2. Методом Даламбера найти форму однородной бесконечной струны, определяемой волновым уравнением
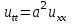, если в начальный момент времени форма струны и скорость точек струны соответственно
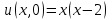и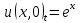 
.Решение
По формуле Даламбера решение начальной задачи для волнового уравнения имеет вид:
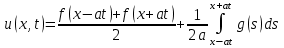.В условии задачи
, 
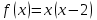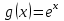, тогда:
,
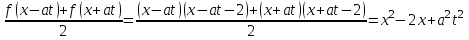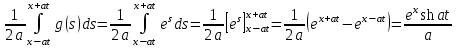.Таким образом, решение задачи имеет вид:
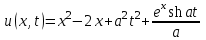.Ответ:
.
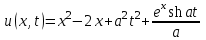