Файл: Петя написал на доске верное равенство 351041421250, а затем вычел из обеих частей по 4 351045421254. Он заметил, что в левой части равенства все числа делятся на 5, а в правой на 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 68
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 lesson
Петя написал на доске верное равенство: 35+10-41=42+12-50, а затем вычел из обеих частей по 4: 35+10-45=42+12-54. Он заметил, что в левой части равенства все числа делятся на 5, а в правой - на 6. Тогда он вынес в левой части 5 за скобки, а в правой - 6 и получил 5(7+2-9)=6(7+2-9). Сократив обе части на общий множитель, Петя получил, что 5=6. Где он ошибся?
Старый сапожник Карл сшил сапоги и послал своего сына Ганса на базар – продать их за 25 талеров. На базаре к мальчику подошли два инвалида (один без левой ноги, другой – без правой) и попросили продать им по сапогу. Ганс согласился и продал каждый сапог за 12,5 талеров.
Когда мальчик пришёл домой и рассказал всё отцу, Карл решил, что инвалидам надо было продать сапоги дешевле – каждому за 10 талеров. Он дал Гансу 5 талеров и велел вернуть каждому инвалиду по 2,5 талера.
Пока мальчик искал на базаре инвалидов, он увидел, что продают сладости, не смог удержаться и истратил 3 талера на конфеты. После этого он нашёл инвалидов и отдал им оставшиеся деньги – каждому по одному талеру. Возвращаясь домой, Ганс понял, как нехорошо он поступил. Он рассказал всё отцу и попросил прощения. Сапожник сильно рассердился и наказал сына, посадив его в тёмный чулан.
Сидя в чулане, Ганс задумался. Получалось, что раз он вернул по одному талеру, то инвалиды заплатили за каждый сапог по 11,5 талеров:
12,5 – 1 = 11,5. Значит, сапоги стоили 23 талера: 2·11,5 = 23. И 3 талера Ганс истратил на конфеты, следовательно, всего получается 26 талеров:
23 + 3 = 26. Но ведь было-то 25 талеров! Откуда же взялся лишний талер?
У деда Мороза бесконечное число конфет. За минуту до Нового года дед Мороз дает детям 100 конфет, а Снегурочка одну конфету отбирает. За полминуты до наступления Нового года дед Мороз дает детям еще 100 конфет, а Снегурочка снова одну конфету отбирает. То же самое повторяется за 15 секунд, за 7,5 секунд и т.д. до Нового года. Докажите, что Снегурочка сможет к Новому году отобрать у детей все конфеты.
Башенные часы отбивают три удара за 12 с. В течение какого времени они пробьют шесть ударов?
31-го декабря Антон сказал, что после Нового Года всё, сказанное им до Нового Года станет ложью. Правду ли он сказал?
В равенстве 101 – 102 = 1 передвиньте одну цифру так, чтобы оно стало верным.
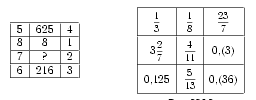
Поняв принципы, по которым составлены таблички чисел, изображённые на рисунках, в первую табличку вставьте недостающее число, а из второй уберите лишнее число.
Расшифруйте ребус, изображённый на схеме.
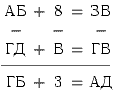
Как-то раз Таня ехала в поезде. Чтобы не скучать, она стала зашифровывать названия разных городов, заменяя буквы их порядковыми номерами в алфавите. Когда Таня зашифровала пункты прибытия и отправления поезда, то с удивлением обнаружила, что они записываются с помощью всего лишь двух цифр: 21221-211221. Откуда и куда шёл поезд?
Найдите значение дроби В*А*Р*Е*Н*Ь*Е / К*А*Р*Л*С*О*Н, где разные буквы – это разные цифры, а между буквами стоит знак умножения.
Дано трехзначное число ABB, произведение цифр которого — двузначное число AC, произведение цифр этого числа равно C (здесь, как в математических ребусах, цифры в записи числа заменены буквами; одинаковым буквам соответствуют одинаковые цифры, разным — разные). Определите исходное число.
Девочка заменила каждую букву в своём имени её номером в русском алфавите. Получилось число 2011533. Как её зовут?
Какое слово зашифровано: 222122111121? Каждая буква заменена своим номером в русском алфавите.
Может ли быть верным равенство
К х О х Т = У х Ч х Ё х Н х Ы х Й
если в него вместо букв подставить цифры от 1 до 9? Разным буквам соответствуют разные цифры.
Перед вами замок "с секретом" (см. рисунок).
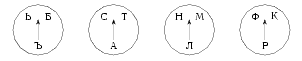
Если вы поставите стрелки на нужные буквы, то получите ключевое слово и замок откроется. Какое это слово?
Директор завода, рассматривая список телефонных номеров и фамилий своих сотрудников, заметил определённую взаимосвязь между фамилиями и номерами телефонов. Вот некоторые фамилии и номера телефонов из списка:
| Ачинский | 8111 |
| Бутенко | 7216 |
| Галич | 5425 |
| Лапина | 6131 |
| Мартьянов | 9143 |
| Ромидзе | 7186 |
Какой номер телефона у сотрудника по фамилии Огнев?
Расшифруйте ребус: КИС+КСИ=ИСК. Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Замените буквы в слове ТРАНСПОРТИРОВКА цифрами (разным буквам соответствуют разные цифры, а одинаковым одинаковые) так, чтобы выполнялось неравенство Т > Р > А > Н < С < П < О < Р < Т > И > Р > О < В < К < А.
Ребус-система. Расшифруйте числовой ребус — систему
Может ли быть верным равенство К×О×Т = У×Ч×Е×Н×Ы×Й, если вместо букв в него подставить цифры от 1 до 9 (разным буквам соответствуют разные цифры)?
Может ли быть верным равенство К×О×Т = У×Ч×Е×Н×Ы×Й, если в него вместо букв подставить цифры от 1 до 9? Разным буквам соответствуют разные цифры.
Когда Незнайку попросили придумать задачу для математической олимпиады в Солнечном городе, он написал ребус (см. рисунок). Можно ли его решить? (Разным буквам должны соответствовать разные цифры.)
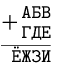
В записи *1*2*4*8*16*32*64 = 27 вместо знаков ''*'' поставьте знаки ''+'' или ''-'' так, чтобы равенство стало верным.
Шифр кодового замка является двузначным числом. Буратино забыл код, но помнит, что сумма цифр этого числа, сложенная с их произведением, равна самому числу. Напишите все возможные варианты кода, чтобы Буратино смог быстрее открыть замок.
Решите ребус: АХ×УХ = 2001.
Расставьте скобки и знаки арифметических действий так, чтобы получилось верное равенство:
Можно ли заменить буквы цифрами в ребусе
ШЕ· СТЬ + 1=СЕ· МЬ
так, чтобы получилось верное равенство (разные буквы нужно заменять разными цифрами, одинаковые буквы — одинаковыми цифрами)?
Буратино правильно решил пример, но испачкал свою тетрадь.
За каждой кляксой скрывается одна и та же цифра, отличная от нуля. Найдите эту цифру.
Решить ребус
AC · CC · K = 2002 (разным цифрам соответствуют разные буквы и наоборот).
Ребус. Решите числовой ребус АААА−ВВВ+СС−К=1234 (разным буквам соответствуют разные цифры, а одинаковым одинаковые)
Найдите наименьшее четырёхзначное число СЕЕМ, для которого существует решение ребуса МЫ + РОЖЬ = СЕЕМ. (Одинаковым буквам соответствуют одинаковые цифры, разным — разные.)
Укажите какое-нибудь решение ребуса: 2014 + ГОД = СОЧИ.
В записи * + * + * + * + * + * + * + * = ** замените звёздочки различными цифрами так, чтобы равенство было верным.
К некоторому числу прибавили его сумму цифр и получили 2014. Приведите пример такого числа.
Расшифруйте ребус, изображённый на рисунке. Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Расшифруйте ребус:
Восстановите цифры. Восстановите цифры в следующем примере на деление
Решите ребус: БАО×БА×Б = 2002.
В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведение получившихся чисел оказалось равным 2007. Какая отметка выходит у Вовочки в четверти по пению? ("Колов" учительница пения не ставит.)
КУБ является кубом. Докажите, что ШАР кубом не является. (КУБ и ШАР трёхзначные числа, разные буквы обозначают различные цифры.)
Найдите все решения ребуса Я + ОН + ОН + ОН + ОН + ОН + ОН + ОН + ОН = МЫ.
(Одинаковыми буквами зашифрованы одинаковые цифры, разными разные.)
Замените знаки вопроса соответствующими буквами или словами:
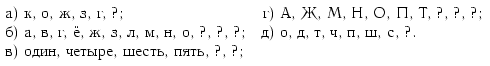
Паша записал на доске пример на сложение, после чего заменил некоторые цифры буквами, причём одинаковые цифры – одинаковыми буквами, а различные цифры – различными буквами. У него получилось: КРОСС + 2011 = СТАРТ
. Докажите, что Паша ошибся.
\
3 lesson
АРФА, БАНТ, ВОЛКОДАВ, ГГГГ, СОУС. Из этих пяти "слов" четыре составляют закономерность, а одно — лишнее. Попробуйте найти это лишнее слово. Интересно, что задача имеет пять решений, т.е. про каждое слово можно объяснить, почему именно оно лишнее, и какой закономерности подчиняются остальные четыре слова.
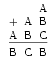
Витя выложил из карточек с цифрами пример на сложение и затем поменял местами две карточки. Как видите, равенство нарушилось. Какие карточки переставил Витя?
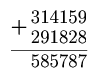
Отличник Поликарп и двоечник Колька составляли минимальное 5-значное число, которое состоит из различных чётных цифр. Поликарп своё число составил правильно, а Колька ошибся. Однако оказалось, что разность между Колькиным числом и правильным ответом меньше 100. Какие числа составили Поликарп и Колька?
Используя пять двоек, арифметические действия и возведение в степень, составьте числа от 1 до 26.
Используя пять троек, арифметические действия и возведение в степень, составьте числа от 1 до 39.
Используя пять четвёрок, арифметические действия и возведение в степень, составьте числа от 1 до 22.
Используя пять пятёрок, арифметические действия и возведение в степень, составьте числа от 1 до 17.
Используя пять шестёрок, арифметические действия и возведение в степень, составьте числа от 1 до 14.
Используя пять семёрок, арифметические действия и возведение в степень, составьте числа от 1 до 22.
Используя пять восьмёрок, арифметические действия и возведение в степень, составьте числа от 1 до 20.
Используя пять девяток, арифметические действия и возведение в степень, составьте числа от 1 до 13.
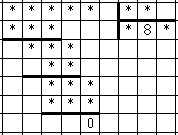
Весь комплект косточек домино, кроме 0-0, уложили так, как изображено на рисунке. Разным буквам соответствуют разные цифры, одинаковым — одинаковые. Сумма очков в каждой строке равна 24. Попробуйте восстановить цифры.

Автобусный билет будем считать счастливым, если между его цифрами можно в нужных местах расставить знаки четырёх арифметических действий и скобки так, чтобы значение полученного выражения равнялось 100. Является ли счастливым билет N123456?