50) .Средняя и предельная ошибки выборки для варьирующего и альтернативного признаков. Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами: N – объем генеральной совокупности (число входящих в нее единиц); n – объем выборки (число обследованных единиц); - генеральная средняя (среднее значение признака в генеральной совокупности); 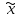- выборочная средняя; p– генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности); w – выборочная доля. Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности: 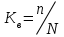. Обычно используют: среднюю величину количественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются наличием изучаемого признака). Выборочная доля ( w ) определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п: w = т / п . Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки. Ошибка выборки 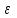или, иначе говоря, ошибка репрезентативности - разность соответствующих выборочных и генеральных характеристик: для средней количественного признака 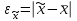; для доли (альтернативного признака) 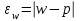. Выборочная средняя и выборочная доля - случайные величины принимающие различные значения в зависимости от того, какие единицы совокупности попали в выборку. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки. Средняя ошибка выборки при повторном отборе рассчитывается по следующим формулам: для средней количественного признака: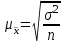

---

; для доли (альтернативного признака): 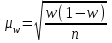. Средняя ошибка выборки при бесповторном отборе рассчитывается по следующим формулам: для средней качественного признака 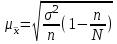; для доли (альтернативного признака) 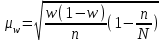. В каждой конкретной выборке расхождение между выборочной средней и генеральной 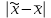может быть меньше средней ошибки 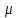, равно ей или больше ее. Каждое из этих расхождений имеет различную вероятность. Поэтому фактические расхождения между выборочной средней и генеральной рассматривают как предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью Р. Предельную ошибку выборки можно рассчитать по следующим формулам: при повторном отборе: для средней 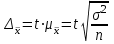, где t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки; 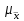- средняя ошибка выборки; для доли 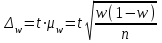; при бесповторном отборе: для средней 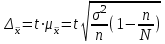; для доли 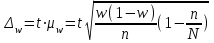. При вероятности 0,683 коэффициент t = 1; при вероятности 0,954 коэффициент t = 2; при вероятности 0,997 коэффициент t = 3. Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы: для средней 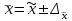; ; 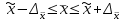для доли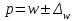

---

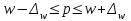; . Наряду с абсолютным значением предельной ошибки выборки рассчитывается также и предельная относительная ошибка выборки (процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности: для средней), %: 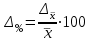; для доли, %: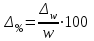

51) Понятие о вариации признака в статистической совокупности. Система показателей вариации. Применение в анализе финансово-экономической деятельности предприятий.

Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации. Самым элементарным показателем вариации признака является размах вариации R, 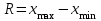.Размах вариации показывает лишь крайние отклонения признака. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Это среднее линейное отклонение 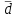(среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической). Среднее линейное отклонение для несгруппированных данных: 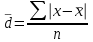, где п – число членов ряда; для сгруппированных данных: 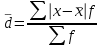, где 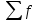- сумма частот вариационного ряда. Дисперсияпризнака - средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий. Простая дисперсия для несгруппированных данных: ; взвешенная дисперсия для вариационного ряда

---

: . Cвойства дисперсии: 1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, дисперсия не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (iраз), то дисперсия уменьшится или увеличится в 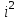раз. Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов: 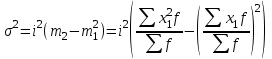, где i – величина интервала; 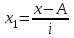-новые (преобразованные) значения вариантов (А – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой); 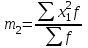- момент второго порядка; 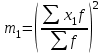- квадрат момента первого порядка. Среднее квадратическое отклонение 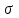равно корню квадратному из дисперсии: для несгруппированных данных: 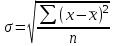, для вариационного ряда: 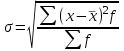. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Исчисляем среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака 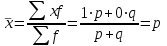. Дисперсия альтернативного признака: 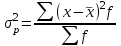. Подставив в формулу дисперсии q = 1 – p, получим 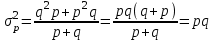. Таким образом, 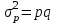- дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком. Среднее квадратическое отклонение альтернативного признака 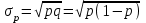. Для сравнения вариаций различных признаков, используют относительный показатель вариации – коэффициент вариации.

---

Коэффициент вариации отношение среднего квадратического отклонения к средней арифметической: 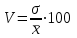. Также коэффициент вариации используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

№ 52

Биржевые статистические показатели: количество эмитентов, ценных бумаг, объем совершенных сделок, количество проданных ценных бумаг, средняя сумма сделок, оборачиваемость ценных бумаг. По закону «о рынке ценных бумаг» эмитент – юридическое лицо, органы исполнительной власти или органы местного самоуправления, несущие от своего имени обязательство перед владельцами ценных бумаг по осуществлению прав, закрепленных за ними. Он всегда только продавец. Инвесторам принадлежат ценные бумаги, делятся на индивидуальных (физических лиц), институциональных (коллективных) и профессионалов (брокеры, дилеры, управляющие ценными бумагами, определяющие взаимные обязательства – клиринг, ведущие реестра владельцев бумаг, депозитарии, торговцы). Количество участников должно быть не менее 1000, чистые активы эмитента ценных бумаг не менее 20 млн. евро. Стоимость чистых активов должна быть больше уставного капитала, срок эмитента не менее 3 лет. Для включения ценной бумаги в котировальный лист размер чистых активов не менее 2 млн. евро, стоимость их не меньше уставного капитала, срок существование не менее 2 лет, количество участников не менее 500. При использовании услуг специалиста, при подачи документов на листинг должен указать участника торгов. Специалист – участник торгов заключивший с биржей договор (соглашение). Обобщающим показателем динамики курсов ценных бумаг является индексы рассчитываемые биржами или специализированными фирмами. Они показывают состояние экономики страны и состояние портфеля ценных бумаг инвестора. Это статистическая средняя, рассчитанная на основе курсовой стоимости ценных бумаг. Через определенные промежутки времени курсовая стоимость составляющих индеек акций фиксируется для расчета значения индекса. Биржа рассчитывает его на основе котируемых акций. Они насчитывают как большое число бумаг (с широкой базой), так и небольшое число с узкой базой. Рассчитывают большинство индексов – произведение цены акции на их количество. Значит цена акции взвешивается по их количеству. Курсовая стоимость ценных бумаг отражает результаты действий выпустивших их кампаний.

---

Смотрите также файлы

• Доходы банка.docx

• Выносливость.docx

• Практическое задание 1 Преподаватель Астахова Мария Александровна.docx

• Письма и телефонограммы.docx

• Контрольная работа дисциплина (модуль) Стандартизация и сертификация в сервисе наименование учебной дисциплины (модуля).docx