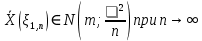Рассмотрим выборки из генеральных совокупностей объемом 50 ед: - число бракованных деталей в партии (штук), - продолжительность работы прибора до первого отказа (часов), - время ожидания пассажиром транспорта (минут)Рисунок1- Фрагмент исходных данныхРассмотрим х1,n- наблюденные значения случайной величины ξ1.Так как случайная величина ξ1 - число бракованных деталей в партии (штук) является дискретной, то группировку выборочных данных проведем в форме дискретного вариационного ряда. 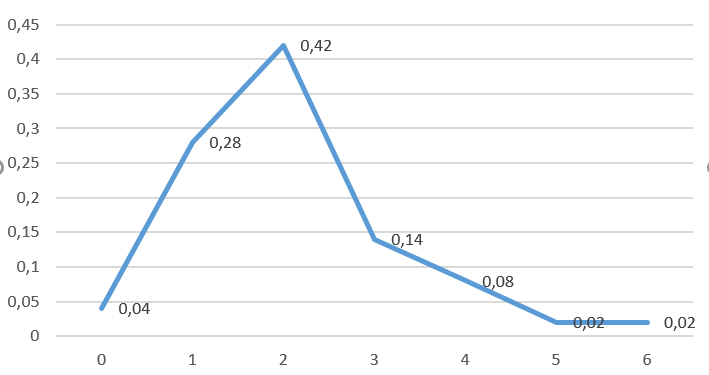Упорядочим по возрастанию элементы апостериорной выборки.В итоге получим упорядоченную выборку х1,n={0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,4,4,4,4,5,6}Далее составим дискретный вариационный ряд частот, относительных частот:Таблица1-Дискретный вариационный ряд частотПостроим полигон относительных частот:Рисунок 2 - Полигон относительных частот, построенный на основе выборки из генеральной совокупностиНайдем накопленные относительные частоты:Таблица 2 – Дискретный вариационный ряд частотТаким образом, эмпирическая функция распределения примет следующий вид: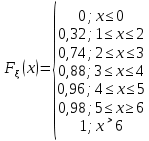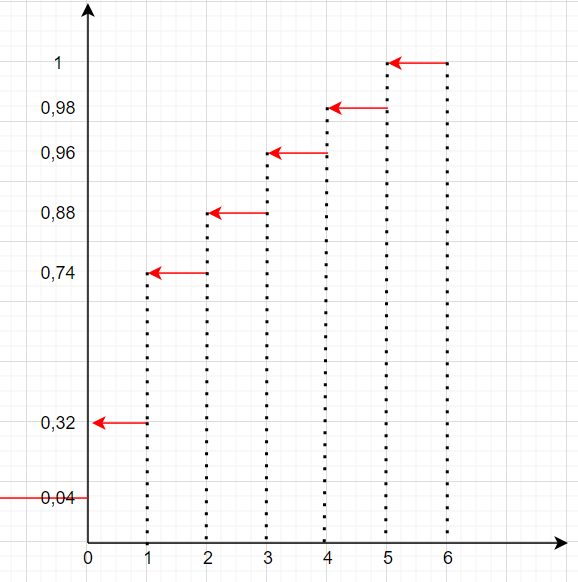Рисунок 3- График эмпирической функции распределения, построенный на основе выборки из генеральной совокупностиПо полигону относительных частот можно сделать предположение, что случайная величина ξ1 имеет биномиальное распределение.Рассмотрим х2,n- наблюденные значения случайной величины ξ2.Так как случайная величина ξ2 - продолжительной работы прибора до первого отказа (часов) является непрерывной, то группировку выборочных данных следует провести в форме интервального вариационного ряда.

---

Упорядочим по возрастанию элементы апостериорной выборки.В итоге получим упорядоченную выборку х2,n={12,81; 13,32; 13,35; 13,69; 14,39; 14,79; 15,23; 15,24; 15,69; 16,43; 16,61; 16,64; 17,06; 17,09; 17,3; 17,76; 18; 18,12; 18,32; 18,5; 18,73; 18,73; 18,77; 18,82; 18,85; 19,05; 19,21; 19,71; 20,16; 20,24; 20,65; 21,21; 21,72; 21,77; 21,94; 21,96; 22,06; 22,71; 22,72; 22,86; 22,96; 23,08; 23,31; 23,42; 23,85; 24,27; 24,65; 25,7; 25,9; 26,43}Построим интервальный вариационный ряд частот, относительных частот, плотности относительных частот, выполняя следующие действия: а) Рассчитаем количество интервалов , воспользовавшись формулой Стэрджесса: 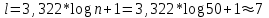Так, получили 7 интервалов.б) Рассчитаем длину интервалов h: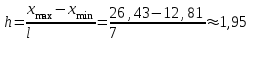в) Найдем границы интервалов: v₀=x_min,….. , v_i=v_i-1+h,….,v_l=v_l-1+hТаким образом получим границы интервалов: v₀=x_min= 12,81 ,….. , v₁= 12,81+1,95=14,76, v₂=14,76+1,95=16,71, v₃=16,71+1,95=18,66 v₄=18,66+1,95 =20,61 , v₅=20,61+1,95=22,56, v₆=22,56+1,95=24,51, v₇=24,51+1,95=26,46 и составим 1первую строчку таблицы 2 Таблица 2 - Интервальный вариационный ряд частот

[vi-1;vi)	[12,81; 14,76)	[14,76; 16,71)	[16,71; 18,66)	[18,66; 20,61)	[20,61; 22,56)	[22,56; 24,51)	[24,51; 26,46)
Частоты ni	5	7	8	10	7	9	4

г) Найдем частоты n_i. Для этого посчитаем, сколько значений попало в каждый интервал (вторая строчка таблицы 2).

---

д) Посчитаем относительные частоты по формуле (1) и плотности относительных частот f_i по формуле (8):f_i= P_i^*/ (v_i- v_i-1) (8)е) Составим таблицу интервального вариационного ряда частот, относительных частот, плотности относительных частот (таблица 3). Таблица 3 - Интервальный вариационный ряд, построенный на основе выборки из генеральной совокупности 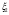i=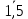

[vi-1;vi)	[12,81; 14,76)	[14,76; 16,71)	[16,71; 18,66)	[18,66; 20,61)	[20,61; 22,56)	[22,56; 24,51)	[24,51; 26,46)
Частоты ni	5	7	8	10	7	9	4
Относительные частоты Pi*= ni/n	0,1	0,14	0,16	0,2	0,14	0,18	0,08
fi= Pi*/ (vi- vi-1)	0,0513	0,0718	0,0821	0,1026	0,0718	0,0923	0,0410

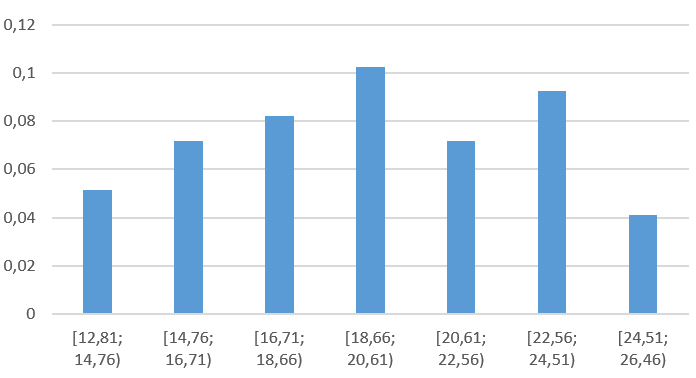
Рисунок 4 - Гистограмма плотности относительных частот, построенная на основе выборки из генеральной совокупности ξ2.По гистограмме можно сделать предположение, что случайная величина ξ2 имеет экспоненциальное распределение.Определение основных выборочных характеристик

1. 
   Случайная величина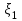 - число бракованных деталей в партии (штук) – дискретная случайная величина.
   

Объем выборки: n=50.Дискретный вариационный ряд частот и относительных частот имеет следующий вид:

---

_{Таблица 4 –} дискретный вариационный ряд, построенный на основе выборки из генеральной совокупности

Варианты х(i)	0	1	2	3	4	5	6
Частоты ni	2	14	21	7	4	1	1

Рассчитаем точечные оценки:Рассчитаем оценку математического ожидания:

1. 
   Рассчитаем оценку дисперсии:
   

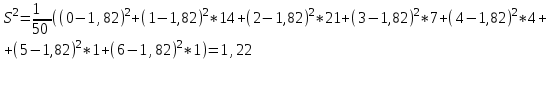
а) несмещенная оценка дисперсииб) смещенная оценка дисперсии

2. 
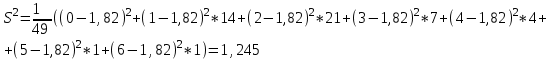
   Рассчитаем оценку среднего квадратического отклонения
   

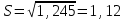
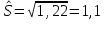
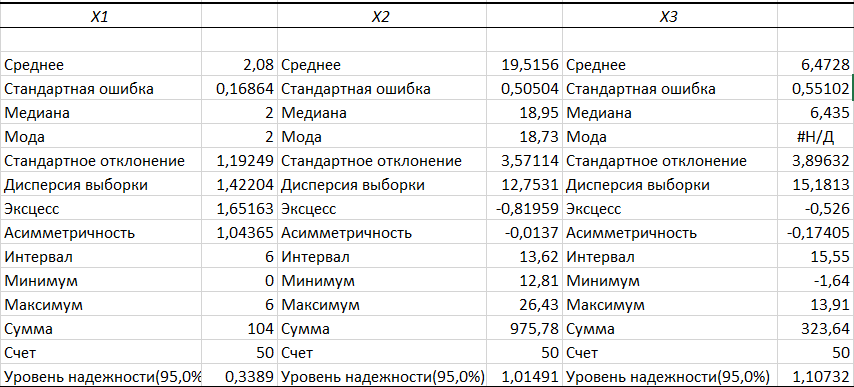
а) смещенная_{б) несмещенная}Реализовав расчет основных числовых характеристик с помощью пакета Excel, получили значения, которые совпадают со значениями, полученными выше. Таким образом, на основе точечной оценки математического ожидания можно сделать вывод о том, что среднее число бракованных деталей в партии равно приблизительно 2 штуки. Наиболее часто встречающееся количество бракованных деталей в партии равно 2. Сравнивая оценки мат.ожидания, моды и медианы можно отметить, что данные характеристики отличаются, что указывает на не симметричность распределения относительно среднего значения. Так как точечная оценка коэффициента асимметрии генеральной совокупности 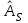>0, то сделаем вывод, что наблюдается правосторонняя асимметрия.

---

Полученные выводы подтверждают предположение относительно биномиального закона распределения.

2. 
   Случайная величина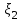 - продолжительность работы прибора до первого отказа (часов) – непрерывная случайная величина.
   

Объем выборки: n=50.Интервальный вариационный ряд плотности относительных частот имеет следующий вид: табл.8-интервальный вариационный ряд, построенный на основе выборки из генеральной совокупности

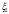
[vi-1;vi)	[12,81; 14,76)	[14,76; 16,71)	[16,71; 18,66)	[18,66; 20,61)	[20,61; 22,56)	[22,56; 24,51)	[24,51; 26,46)
Частоты ni	5	7	8	10	7	9	4

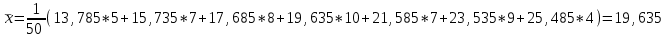
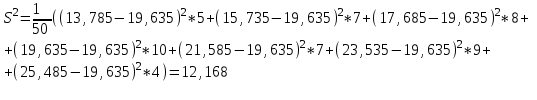
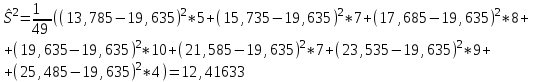
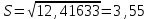
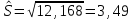
Рассчитаем точечные оценки :1)Рассчитаем оценку математического ожидания: 2)Рассчитаем оценку дисперсии:а) смещенная оценка дисперсииб) несмещенная оценка дисперсии3)Рассчитаем оценку среднего квадратического отклоненияа) смещеннаяб) несмещеннаяРезультаты построения доверительных интервалов1)Случайная величина - число бракованных деталей в партии (штук) –дискретная случайная величина.Объем выборки: n=50.Согласно центральной предельной теореме можно считать, что генеральная совокупность распределена нормально.

---

Смотрите также файлы

• По учебному курсу История.docx

• Качество жизни и уровень жизни человека сравнение понятий..docx

• Акт по рассмотрению обращения Жолнерович Н. А. проживающей в квартире 81.doc

• Теоретические основы дисциплины Введение в профессию.docx

• Производство в суде апелляционной инстанции (действующее и вводимое с 01. 01. 2013 г.).docx