ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Построим доверительный интервал для математического ожидания при неизвестной дисперсии с доверительной вероятностью .
Построим статистику:
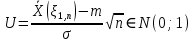
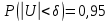
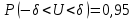
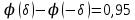
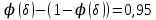
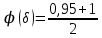
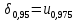
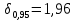
Составим доверительный интервал по формуле:
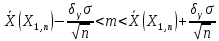
Так как неизвестно и n – велико, то мы в дальнейшем будем использовать оценку дисперсии –S.
X̅(X 1,n)=2,08; S(X 1,n)=1,19
2,08- 1,96*1,19/√49˂m˂2,08+1,96*1,19/√49
1,75˂m˂2,41
Таким образом, с вероятностью
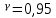можно утверждать, что число бракованных деталей в партии заключено в интервале (1,75;2,41).-
Случайная величина - продолжительность работы прибора до первого отказа (часов) – непрерывная случайная величина.Объем выборки: n=50.
При большом объёме выборки генеральная совокупность распределена нормально.
а) Построим доверительный интервал для математического ожидания при неизвестной дисперсии с доверительной вероятностью .
Согласно центральной предельной теореме можно считать, что генеральная совокупность распределена нормально.
Построим доверительный интервал для математического ожидания при неизвестной дисперсии с доверительной вероятностью .
Построим статистику:
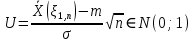
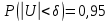
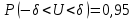
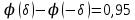
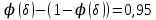
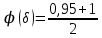
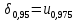
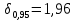
Составим доверительный интервал по формуле:
Так как доверительный интервал содержит неизвестный параметр , то при большом объеме выборки n среднеквадратическое отклонение
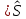:̅(X 1,n)=19,5; Sˆ(X 1,n)=3,57
19,5 - 1,96*3,57/√49˂m˂19,5+1,96*3,57/√49
18,5˂m˂20,5
Таким образом, с вероятностью
можно утверждать, что средняя продолжительность работы прибора до первого отказа заключена в интервал (18,5;20,5).