Контрольная работа по дисциплине «Социально-экономическая статистика»
Вариант N 4.
Задание 1.

Составить комбинационную таблицу на основе следующих данных. На начало 2015/2016 учебного года в российских государственных и муниципальных высших образовательных учреждениях обучалось 95 781 человек иностранцев. Граждан стран СНГ обучалось на очных отделениях 23 468 человек, по другим формам обучения – 24 771 человек. Граждан стран «дальнего зарубежья» на очных отделениях обучалось 44 103 человека и по остальным формам обучения – 3439 человек.

Решение.

Комбинированные таблицы содержат отдельные группы и подгруппы, на которые подразделяются экономические показатели, характеризующие изучаемое экономическое явление. При этом такое подразделение осуществляется не по одному, а по нескольким признакам.

В нашем случае такими признаками будут формы обучения и гражданство.

Таблица 1.1 – Состав обучающихся в российских государственных и муниципальных высших образовательных учреждениях.

Гражданство обучающихся	Количество обучающихся	Количество обучающихся в % к итогу
Граждане СНГ	48239	50,4
- очное отделение	23468	24,5
- другие формы обучения	24771	25,9
Граждане стран "дальнего зарубежья"	47542	49,6
- очное отделение	44103	46,0
- другие формы обучения	3439	3,6
Итого	95781	100,0

Задание 2.

Имеются данные о работе двух организаций. Требуется определить средние значения всех представленных в таблице признаков.

Предприятие	Выпуск продукции			Фактическая выработка продукции на одного рабочего, тыс. руб.
	По плану, тыс. руб.	По факту, тыс. руб.	Процент выполнения плана
	П	Ф	В	Т
1	5400	6000	111,1	3
2	7400	8000	108,1	3,5
3	9400	10000	106,4	4

---

Решение.

В этом примере единица совокупности – одно предприятие, поэтому среди представленных в таблице признаков первичными являются плановый и фактический объемы выпускаемой продукции. Следовательно, для расчета средней величины каждого из этих признаков нужно применить формулу простой средней:





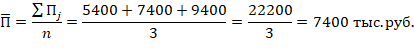
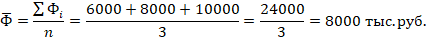
где – число предприятий.

Следующий признак в таблице – процент выполнения плана, который представляет собой относительную величину, рассчитанную по формуле




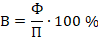
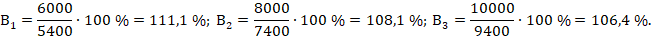
Среднее значение процента выполнения плана по совокупности предприятий можно представить в виде отношения обобщенных значений тех же признаков, каждое из которых охватывает всю изучаемую совокупность единиц:



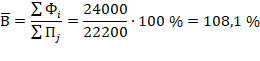
Поскольку единицей совокупности, как уже отмечалось, в нашем примере является одно предприятие, выработка одного рабочего – это вторичный признак. Отсюда для расчета ее среднего значения нужно применить формулу взвешенной средней. Исходными для такого расчета будет следующее соотношение:



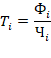
где – численность рабочих предприятия.

В соответствии с рассмотренной выше методикой определения средней величины вторичного признака можно записать:



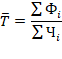
Для определения средней выработки одного рабочего необходимо предварительно вычислить численность рабочих, занятых на каждом предприятии. В соответствии с исходными данными это можно сделать по формуле



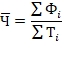
Проведя необходимую подстановку, получаем следующее выражение искомой средней, которое соответствует формуле средней гармонической взвешенной:

---

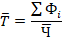
Подставив в формулу числовые значения, находим



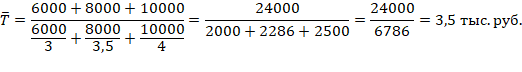
Задание 3.

При обследовании студентов второго курса по возрасту были зафиксированы следующие данные:

18 20 20 19 18 20 20 19 18 18 21 19 21 20 18 19 18 19 21 21 18 18 18 18 22 19 18 20 18 19 19 21 19 21 20 21 18 19 21 19 19 22 21 19 20 21 18 20 19 19 20 22

Составить вариационный ряд, полигон распределения, кумуляту, огиву.
Решение.

В данном примере вариантами является возраст студентов второго курса. Для определения частот необходимо рассчитать число студентов, имеющих соответствующий возраст.

Возраст студента,	18	19	20	21	22
Количество студентов,	14	15	10	10	3

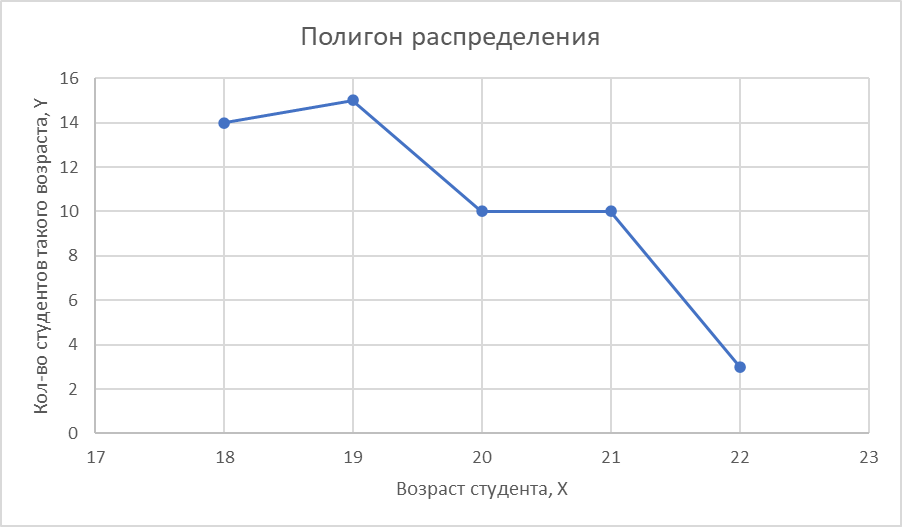
Полигон используется для дискретных вариационных рядов.

Для построения полигона распределения по оси абсцисс откладываем количественные значения варьирующего признака – варианты (возраст студента второго курса), а по оси ординат – частоты или частости.

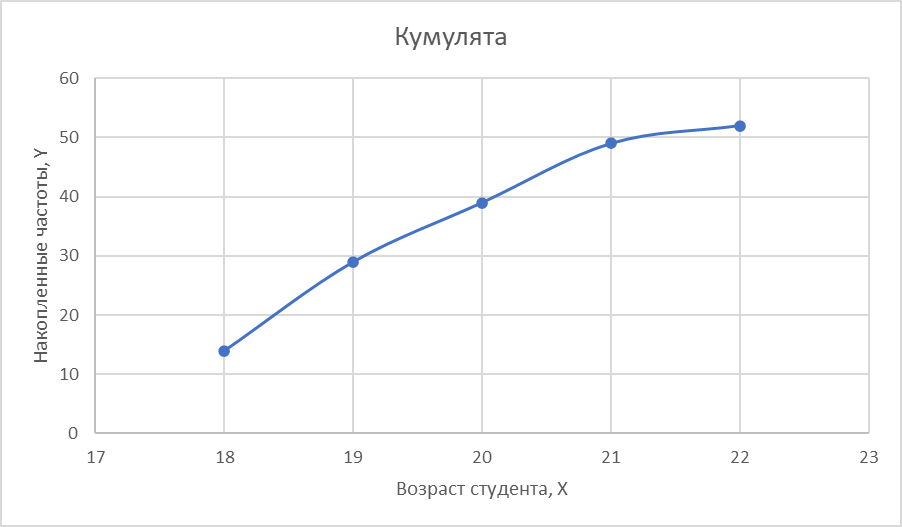
Кумулята – график распределения значений признака по накопленным частотам. Для построения кумуляты необходимо подсчитать значения накопленных частот для каждого значения признака и далее по оси абсцисс отложить значения признака, а по оси ординат – накопленные частоты (частости).

Возраст студента,	18	19	20	21	22
Количество студентов,	14	15	10	10	3
Кумулята	14	29	39	49	52

---

Огива – график, аналогичный кумуляте, координаты которой поменяли местами: по оси абсцисс откладывают накопленные частоты, по оси ординат – значения признака.


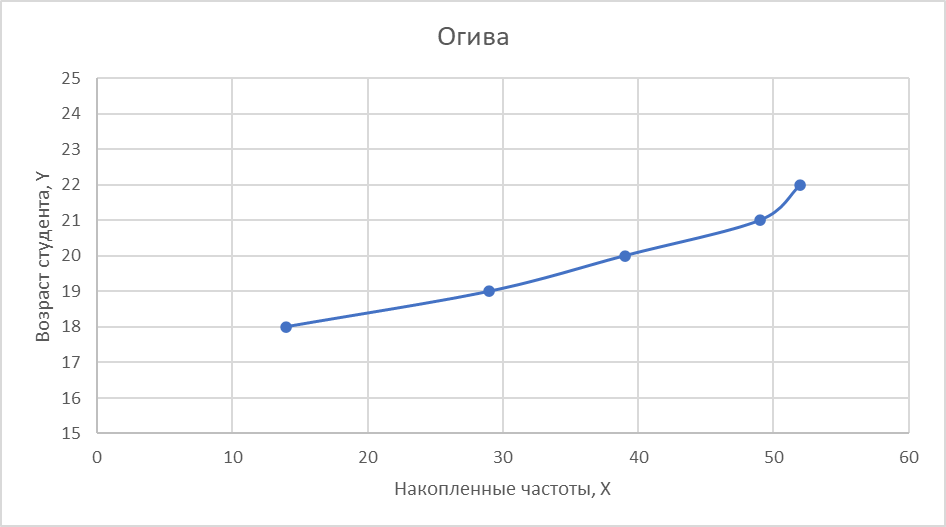
Задание 4.

Имеются данные обследования размера каждого пятого вклада от населения в Сбербанке на конец года:

Размер вклада, руб.	Число вкладов
1000-3000	140
3000-5000	90
5000-7000	160
7000-9000	50
9000 и выше	40

Требуется: 1. Определить средний размер вклада, моду и медиану.

2. Построить графики распределения.
Решение.

Рассчитаем средний размер вклада.

В данном ряду варианты усредняемого признака (размер вклада) представлены не одним числом, а в виде интервала «от – до». Причём последний интервал открытый.

В таких рядах условно принимается, величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей. Таким образом, размер вклада последней группы – от 9000 до 11000 руб. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:



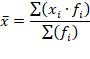
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так для первой группы дискретная величина будет равна:



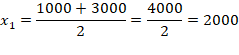
Исходные и расчётные данные представим в таблице:

Размер вклада, руб.	Число вкладов,	Середина интервала,		Сумма накопленных частот
1000-3000	140	2000	280000	140
3000-5000	90	4000	360000	230
5000-7000	160	6000	960000	390
7000-9000	50	8000	400000	440
9000-11000	40	10000	400000	480
Итого	480	---	2400000

---

Средний размер вклада равен:



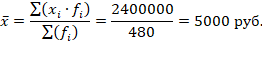
Определим модальное и медианное значение месячного товарооборота.

В интервальных рядах распределения с равными интервалами мода определяется по формуле:



– начальное значение интервала, содержащего моду;

– величина модального интервала,

– частота модального интервала,

– частота интервала, предшествующего модальному,

– частота интервала, следующего за модальным.

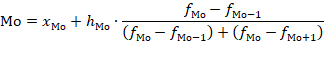
Наибольшее число вкладов (160) имеют величину вклада от 5000 до 7000 руб. Следовательно, этот интервал является модальным интервалом ряда распределения. Введём следующие обозначения:



Подставим эти значения в формулу моды и произведём вычисления:



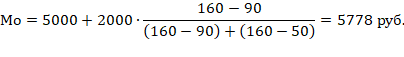
Следовательно, наибольшее число вкладов имеет размер 5778 руб.

Медиана интервального вариационного ряда распределения определяется по формуле:



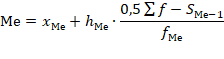
где

– начальное значение интервала, содержащего медиану;

 – величина медианного интервала;

 – сумма частот ряда;

---

Смотрите также файлы

• Перестройка, гласность, итоги.docx

• .docx

• А. С. ЛаппоДанилевского в стране был создан Союз российских архивных деятелей, целью которого стало, с одной стороны, сохранение документального наследия страны, с другой организация архивной службы. При этом предполагалось осуществлять руководство.rtf

• Рецензия на выпускную квалификационную работу.docx

• Правила ведения журнала Именной список личного состава Задачи подразделению на период обучения и на неделю.doc