Файл: Контрольная работа по дисциплине Социальноэкономическая статистика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– сумма накопленных частот, предшествующих медианному интервалу;
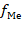– частота медианного интервала.
Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (390), соответствует интервалу 5000 – 7000. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если:
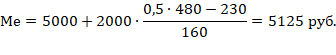
Таким образом, половина вкладов имеет размер менее 5125 руб., а остальные – более 5125 руб.
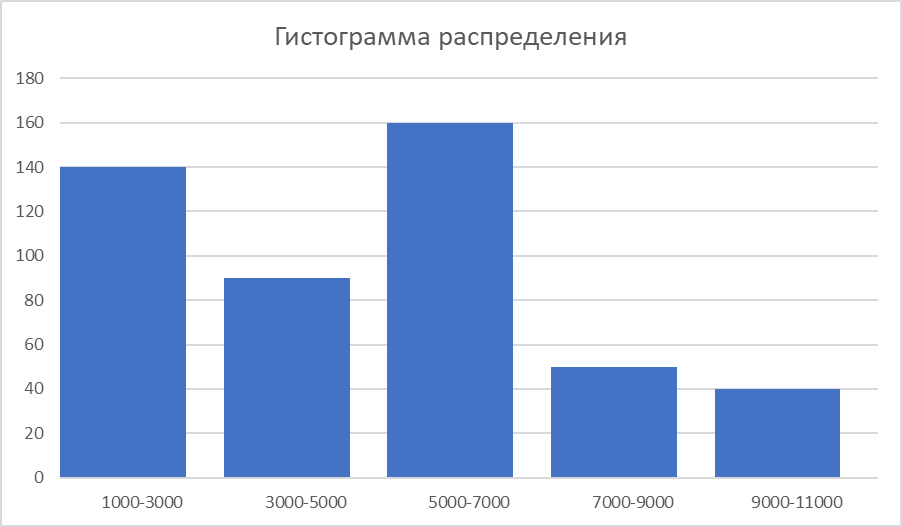
Задание 5.
По данным о распределении сотрудников коммерческого банка по стажу работы определите размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Решение.
Вычислим размах вариации:
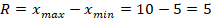
Средний стаж работы сотрудников:
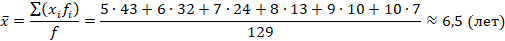
Среднее линейное отклонение вычиляется как средняя арифметическая из абсолютных значений отклонений вариант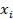
от среднего значения. Для удобства вычислений воспользуемся таблицей:
Определим среднее линейное отклонение.
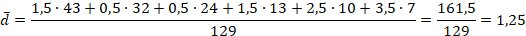
Среднее линейное отклонение стажа работы сотрудников коммерческого банка составит: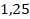
лет, т.е. конкретные значения стажа работы сотрудников в среднем отклоняются от среднего значения признака на 1,25 года.
Расчёт дисперсии произведем по формуле:
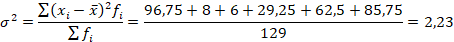
Расчет среднего квадратического отклонения:
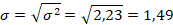
Вычислим коэффициент вариации:
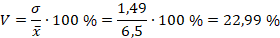
Задание 6.
С целью изучения возможных сдвигов в объеме и структуре потребительского спроса на ноутбуки планируется в следующем месяце провести на территории одного из субъектов РФ выборочное обследование потенциальных покупателей. Будет использована простая случайная выборка.
Необходимо определить, сколько респондентов должно быть опрошено, чтобы с вероятностью 0,9853 гарантировать, что предельные значения ошибок репрезентативности не превысят следующих значений:
по показателю «средняя цена, которую готовы уплатить покупатели» - 2,4 тыс. руб.;
доля покупателей, которые намерены пользоваться услугами сети Интернет, - 14 %;
по показателю «средний возраст потенциальных покупателей» - 2,4 года.
По материалам проведенного в соответствующем месяце прошлого года выборочного обследования среднее квадратическое отклонение составило: по показателю цены покупки - 14 тыс. руб., по показателю среднего возраста покупателей - 17,4 года.
Доля потенциальных пользователей сети Интернет среди покупателей составила 34 %.
Решение.
Расчет необходимого объема выборки следует произвести с использованием формулы для повторного отбора в связи с большим объемом генеральной совокупности, в качестве которой выступают все потенциальные покупатели ноутбуков.
По таблице интеграла вероятности находим значение коэффициента кратности ошибки, которое при доверительной вероятности 0,9853 составит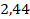
.
Используем следующие формулы для расчета величины
:
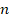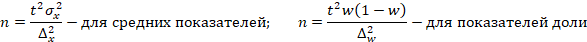
Необходимый и достаточный объем выборки составит:
Для показателя средней цены ноутбука
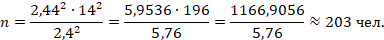
Для показателя среднего возраста
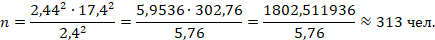
Для показателя доли пользователей сети Интернет
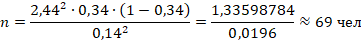
Всем трем показателям удовлетворяет объем выборки в 313 человек. Фактически программой обследования, как правило, предусматривается получение достаточно большого числа обобщающих показателей, но в целях упрощения расчетов в данном условном примере мы ограничились оценками только по трем показателям.
Задание 7.
По результатам выборочного обследования (стратифицированная пропорциональная выборка) качества работы дошкольных детских учреждений в одном из городов Центральной России были получены следующие параметры (данные условные):
На основе приведенных в таблице данных необходимо определить с вероятностью 0,9385:
1) величину предельной ошибки репрезентативности в относительной форме по двум выборочным показателям
, сформулировать вывод о степени точности выборочных данных и правомерности их распространения на генеральную совокупность;
2) доверительные интервалы, в которых находятся по генеральной совокупности два показателя: среднее число детей на одного воспитателя и процент воспитателей со стажем работы в дошкольных учреждениях 5 и более лет;
3) доверительный интервал, в котором находится общая численность детей, посещающих детские сады по генеральной совокупности, если известно, что число воспитателей в среднем на один детский сад составляет по генеральной совокупности 8,4 человека;
4) проверить, являются ли достаточно точными выборочные данные по показателю числа детей на одного воспитателя в пределах каждого типа детских дошкольных учреждений.
Решение.
1) Определение предельной ошибки репрезентативности в относительной форме по двум выборочным показателям.
Первоначально необходимо определить значения средних ошибок репрезентативности по двум показателям.
Выполняем расчет средних ошибок выборки:
*- для средней
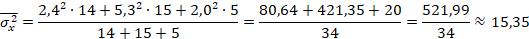
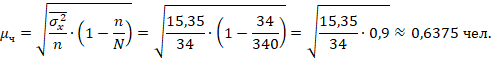
*- дл
– частота медианного интервала.Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (390), соответствует интервалу 5000 – 7000. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если:
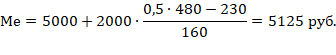
Таким образом, половина вкладов имеет размер менее 5125 руб., а остальные – более 5125 руб.
Задание 5.
По данным о распределении сотрудников коммерческого банка по стажу работы определите размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
| Стаж, лет | 5 | 6 | 7 | 8 | 9 | 10 |
| Число сотрудников | 43 | 32 | 24 | 13 | 10 | 7 |
Решение.
Вычислим размах вариации:
Средний стаж работы сотрудников:
Среднее линейное отклонение вычиляется как средняя арифметическая из абсолютных значений отклонений вариант
от среднего значения. Для удобства вычислений воспользуемся таблицей:| Стаж, лет  | 5 | 6 | 7 | 8 | 9 | 10 | Итого |
| Число сотрудников  | 43 | 32 | 24 | 13 | 10 | 7 | 129 |
 | 215 | 192 | 168 | 104 | 90 | 70 | 839 |
 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | --- |
 | 1,5 | 0,5 | 0,5 | 1,5 | 2,5 | 3,5 | --- |
 | 64,5 | 16 | 12 | 19,5 | 25 | 24,5 | 161,5 |
Определим среднее линейное отклонение.
Среднее линейное отклонение стажа работы сотрудников коммерческого банка составит:
лет, т.е. конкретные значения стажа работы сотрудников в среднем отклоняются от среднего значения признака на 1,25 года.Расчёт дисперсии произведем по формуле:
Расчет среднего квадратического отклонения:
Вычислим коэффициент вариации:
Задание 6.
С целью изучения возможных сдвигов в объеме и структуре потребительского спроса на ноутбуки планируется в следующем месяце провести на территории одного из субъектов РФ выборочное обследование потенциальных покупателей. Будет использована простая случайная выборка.
Необходимо определить, сколько респондентов должно быть опрошено, чтобы с вероятностью 0,9853 гарантировать, что предельные значения ошибок репрезентативности не превысят следующих значений:
по показателю «средняя цена, которую готовы уплатить покупатели» - 2,4 тыс. руб.;
доля покупателей, которые намерены пользоваться услугами сети Интернет, - 14 %;
по показателю «средний возраст потенциальных покупателей» - 2,4 года.
По материалам проведенного в соответствующем месяце прошлого года выборочного обследования среднее квадратическое отклонение составило: по показателю цены покупки - 14 тыс. руб., по показателю среднего возраста покупателей - 17,4 года.
Доля потенциальных пользователей сети Интернет среди покупателей составила 34 %.
Решение.
Расчет необходимого объема выборки следует произвести с использованием формулы для повторного отбора в связи с большим объемом генеральной совокупности, в качестве которой выступают все потенциальные покупатели ноутбуков.
По таблице интеграла вероятности находим значение коэффициента кратности ошибки, которое при доверительной вероятности 0,9853 составит
.Используем следующие формулы для расчета величины
: Необходимый и достаточный объем выборки составит:
Для показателя средней цены ноутбука
Для показателя среднего возраста
Для показателя доли пользователей сети Интернет
Всем трем показателям удовлетворяет объем выборки в 313 человек. Фактически программой обследования, как правило, предусматривается получение достаточно большого числа обобщающих показателей, но в целях упрощения расчетов в данном условном примере мы ограничились оценками только по трем показателям.
Задание 7.
По результатам выборочного обследования (стратифицированная пропорциональная выборка) качества работы дошкольных детских учреждений в одном из городов Центральной России были получены следующие параметры (данные условные):
| Детские сады по формам собственности | Число детских садов | Показатели по выборке | Среднее квадратическое отклонение по показателю «число детей в среднем на 1 воспитателя» | ||
| всего | по выборке | Детей в среднем на одного воспитателя | Процент воспитателей со стажем работы в дошкольных учреждениях 5 лет и более | ||
| Государственные | 140 | 14 | 24 | 25 | 2,4 |
| Муниципальные | 150 | 15 | 25 | 30 | 5,3 |
| Частные | 50 | 5 | 10 | 20 | 2,0 |
На основе приведенных в таблице данных необходимо определить с вероятностью 0,9385:
1) величину предельной ошибки репрезентативности в относительной форме по двум выборочным показателям
, сформулировать вывод о степени точности выборочных данных и правомерности их распространения на генеральную совокупность;
2) доверительные интервалы, в которых находятся по генеральной совокупности два показателя: среднее число детей на одного воспитателя и процент воспитателей со стажем работы в дошкольных учреждениях 5 и более лет;
3) доверительный интервал, в котором находится общая численность детей, посещающих детские сады по генеральной совокупности, если известно, что число воспитателей в среднем на один детский сад составляет по генеральной совокупности 8,4 человека;
4) проверить, являются ли достаточно точными выборочные данные по показателю числа детей на одного воспитателя в пределах каждого типа детских дошкольных учреждений.
Решение.
1) Определение предельной ошибки репрезентативности в относительной форме по двум выборочным показателям.
Первоначально необходимо определить значения средних ошибок репрезентативности по двум показателям.
Выполняем расчет средних ошибок выборки:
*- для средней
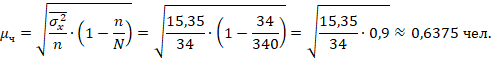
*- дл