Вывод по четвертому заданию: выборочные данные по показателю «среднее числа детей на одного воспитателя» являются достаточно точными и могут быть распространены на генеральную совокупность только по двум типам детских садов — государственным и муниципальным.

---

Задание 8.

Имеются следующие данные о продаже и ценах на продукты на одном из рынков города:

Продукт	Продано, тыс. ед.		Цена единицы, руб.
	в базисном периоде, q0	в отчетном периоде, q1	в базисном периоде, p0	в отчетном периоде, p1
Молоко, л	54	60	34	29
Морковь, кг	4	50	24	19
Говядина, кг	1,4	2	324	300

Определить:

1. Общее изменение физического объема продаж.

2. Общее изменение цен на указанные продукты.

3. Абсолютную экономию населения от снижения цен.
Решение.

1. Общее (в среднем) изменение объема продаж определим по агрегатной формуле индекса физического объема:



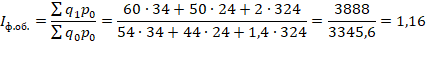
(или 116 %), т.е. в отчетном периоде было продано продуктов на 16 % больше (116 % - 100 % = 16 %), чем в базисном периоде.

2. Общий индекс цен, характеризующий среднее изменение цен на все продукты, определяем по формуле Пааше:



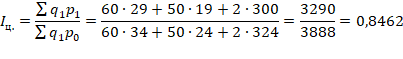
(или 84,62 %), т.е. цены на все продукты снизились в среднем на 15,38 % (84,62 % - 100 % = - 15,38 %).

3. Для ответа на третий вопрос вычтем из числителя агрегатной формулы индекса цен знаменатель:



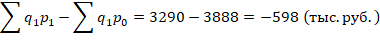
т.е. абсолютная экономия населения от снижения цен составила 598 тыс. руб.

Задание 9.

Имеются следующие данные о выпуске продукции мебельной фабрики:

Наименование изделий	Изменение выпуска в апреле по сравнению с мартом, %	Выпуск продукции в марте, млн. руб., q0p0
Столы	+15	24
Диваны	+14	40
Стулья	+17	34

---

Определить увеличение выпуска всей продукции в апреле по сравнению с мартом (в%), т.е. рассчитать общий индекс физического объема.

Решение.

Общий индекс физического объема может быть рассчитан как средний арифметический:



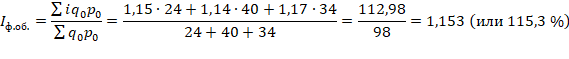
т.е. в целом по предприятию выпуск продукции в апреле по сравнению с мартом увеличен на 15,3 %.

Задание 10.

Служба качества решила определить, одинаково ли надежны динамики мобильных телефонов разных производителей. Было взято по пять телефонных аппаратов каждой из четырех выбранных фирм производителей. Надежность динамиков измеряется с помощью специального устройства, испытывающего их на максимальные нагрузки. Чем дольше работает динамик (время измеряется в условных единицах) до выхода из строя, тем он надежнее.

Результаты испытаний представлены в таблице.

Порядковый номер телефона	Фирма 1	Фирма 2	Фирма 3	Фирма 4
1	20,4	25,4	22,0	26,1
2	19,6	24,4	24,4	21,4
3	23,1	25,4	21,7	18,9
4	19,4	23,9	21,4	22,3
5	20,3	24,	22,6	24,4

Решение.

Для построения таблицы дисперсионного анализа необходимо:

1. Определить выборочные средние для каждой группы

2. Определить среднее время для всех мобильных телефонов.

Для этого просуммируем все 20 показателей и разделим сумму на общее количество наблюдений ( ).

Порядковый номер телефона	Фирма 1	Фирма 2	Фирма 3	Фирма 4
1	20,4	25,4	22,0	26,1
2	19,6	24,4	24,4	21,4
3	23,1	25,4	21,7	18,9
4	19,4	23,9	21,4	22,3
5	20,3	24,	22,6	24,4
Итого	102,8	123,1	112,1	113,1
Среднее арифметическое	20,56	24,62	22,42	22,62

---

Вычислим общую среднюю:



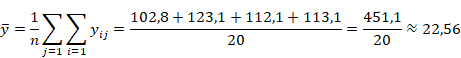
3. Вычислить суммы квадратов отклонений:

- межгрупповая сумма квадратов отклонений:






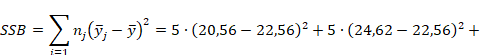
- внутригрупповая сумма квадратов отклонений













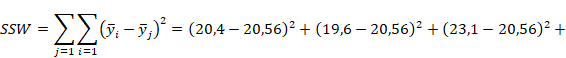
- общая сумма квадратов отклонений



4. Вычислить суммы квадратов отклонений, приходящиеся на одну степень свободы:

- межгрупповая сумма квадратов отклонений:



- внутригрупповая сумма квадратов отклонений:


5. Вычислить -критерий:





При заданном уровне значимости и числе степеней свободы межгрупповой и внутригрупповой вариаций определяется критическое значение -критерия, по таблице значений -критерия Фишера. В рассматриваемом примере числитель имеет три степени свободы

---

, а знаменатель . Таким образом, принимая уровень значимости , т.е. при вероятности ошибочного решения , и , верхнее критическое значение -критерия равно .

Вычисленное значение .

Следовательно, различия между средними значениями времени работы динамиков мобильных телефонов статистически значимы, т.е. нулевая гипотеза отклоняется.

---

Смотрите также файлы

• Перестройка, гласность, итоги.docx

• .docx

• А. С. ЛаппоДанилевского в стране был создан Союз российских архивных деятелей, целью которого стало, с одной стороны, сохранение документального наследия страны, с другой организация архивной службы. При этом предполагалось осуществлять руководство.rtf

• Рецензия на выпускную квалификационную работу.docx

• Правила ведения журнала Именной список личного состава Задачи подразделению на период обучения и на неделю.doc