Вариант 0 дефектов 1 дефект 2 дефекта 3 дефекта более 3

1. 489 144 135 122 110

2. 491 145 134 125 105

3. 489 155 133 123 100

4. 483 153 132 130 102

5. 516 148 131 110 95

6. 508 152 129 111 100

7. 494 147 136 121 102

8. 492 155 128 120 105

9. 471 160 137 122 110

10. 471 159 135 127 108

11. 489 156 131 117 107

12. 486 153 136 119 106

Можно ли с вероятностью 0,99 (при α= 0,01) считать, что партия соответствует стандарту?

ПРИМЕР 4. В MS Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют нормальному закону распределения. Если вычисленная вероятность близка к 1, то можно говорить о высокой степени соответствия экспериментальных данных нормальному закону распределения.

Функция имеет следующие параметры:

ХИ2ТЕСТ (фактический_интервал;ожидаемый_интервал).

Здесь:

- фактический_интервал — это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;

- ожидаемый_интервал — это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.

Проверить соответствие выборочных данных (ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1, пример 1):

64, 57, 63, 62, 58 ,61, 63 ,60, 60, 61, 65, 62, 62 ,60, 64, 61, 59, 59, 63, 61, 62, 58, 58, 63, 61, 59, 62, 60, 60 ,58, 61, 60, 63, 63, 58, 60, 59, 60, 59, 61, 62, 62, 63, 57, 61, 58, 60, 64, 60, 59, 61, 64, 62, 59, 65 нормальному закону распределения.

Решение. (пункты 1-7 решения соответствуют примеру 1 ПРАКТИЧЕСКОГО ЗАНЯТИЯ 1).

1. В ячейку А1 введите слово Наблюдения, а в диапазон А2:Е12— значения веса студентов.

2. Выберите ширину интервала 1 кг. Тогда при крайних значениях веса 57 кг и 65 кг получится 9 интервалов. В ячейки G1 и G2 введите названия интервалов Вес и кг, соответственно. В диапазон G4:G12 введите граничные значения интервалов (57,58,59,60, 61, 62, 63, 64, 65).

3. Введите заголовки создаваемой таблицы: в ячейки Н1:Н2— Абсолютные частоты, в ячейки I1:I2 — Относительные частоты, в ячейки J1:J2— Накопленные частоты.

4. Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек Н4:Н12 (используемая функция ЧАСТОТА задается в виде формулы массива). С панели инструментов Стандартная вызовите Мастер функций (кнопка fx). В появившемся диалоговом окне Мастер функций Выберите категорию Статистические и функцию ЧАСТОТА, после чего нажмите кнопку ОК. Появившееся диалоговое окно ЧАСТОТА необходимо за серое поле мышью отодвинуть вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши в рабочее поле Массив_ данных введите диапазон данных наблюдений (А2:Е12). В рабочее поле Двоичный массив мышью введите диапазон интервалов (G4:G12). Последовательно нажмите комбинацию клавиш Ctrl+Shift+ Enter. В столбце Н4:Н12 появится массив абсолютных частот.

---

5. В ячейке Н13 найдите общее количество наблюдений. Табличный курсор установите в ячейку Н13. На панели инструментов Стандартная нажмите кнопку Автосумма. Убедитесь, что диапазон суммирования указан правильно (Н4:Н12), и нажмите клавишу Enter. В ячейке Н13 появится число 55.

6. Заполните столбец относительных частот. В ячейку I4 введите формулу для вычисления относительной частоты: =Н4/Н$13. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон 15:112. Получим массив относительных частот.

7. Заполните столбец накопленных частот. В ячейку J4 скопируйте значение относительной частоты из ячейки I4 (0,036364). В ячейку J5 введите формулу: =J4 + J5. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон J6:J12, Получим массив накопленных частот.

В результате получится таблица (рис. 3)

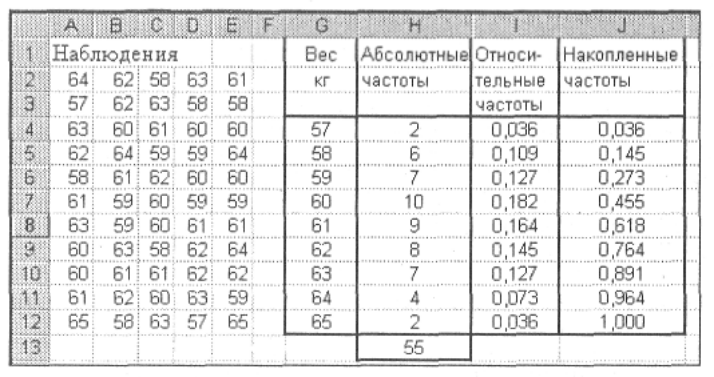
Рис. 3

8. Найдите теоретические частоты нормального распределения. Для этого предварительно необходимо найти среднее значение и стандартное отклонение выборки. В ячейке I13 с помощью функции СРЗНАЧ найдите среднее значение для данных из диапазона А2:Е12 (60,855). В ячейке J13 с помощью функции СТАНДОТКЛОН найдите стандартное отклонение для этих же данных (2,05). В ячейки К1 и К2 введите название столбца— Теоретические частости. Затем с помощью функции НОРМРАСП найдите теоретические частости. Установите курсор в ячейку К4, вызовите указанную функцию и заполните ее рабочие поля: х — G4; Среднее — $1$13; Стандартное_откл — $J$13; Интегральный — 0. Получим в ячейке К4 0,033. Далее протягиванием скопируйте содержимое ячейки К4 в диапазон ячеек К5:К12. Затем в ячейки L1 и L2 введите название нового столбца— Теоретические частоты. Установите курсор в ячейку L4 и введите формулу =Н$13*К4. Далее протягиванием скопируйте содержимое ячейки L4 в диапазон ячеек L5:L12. Результаты вычислений представлены на рис. 4.

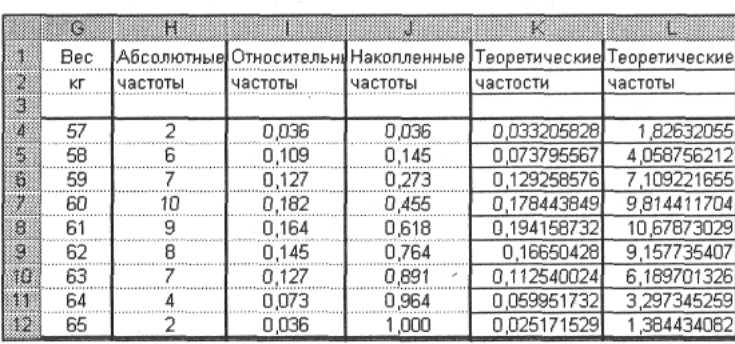
Рис. 4. Результаты вычисления теоретических частостей и частот

С помощью функции ХИ2ТЕСТ определите соответствие данных нормальному закону распределения. Для этого установите табличный курсор в свободную ячейку L13. На панели инструментов Стандартная нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ХИ2ТЕСТ отодвиньте вправо на 1-2 см от данных. Указателем мыши в рабочие поля введите фактический Н4:Н12 и ожидаемые L4:L12 диапазоны частот (рис. 5). Нажмите кнопку ОК. В ячейке L13 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения — 0,9842.

Рис. 5. Пример заполнения рабочих полей функции ХИ2ТЕСТ

9. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,98 много больше, чем уровень значимости ά = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения. Более того, поскольку полученная вероятность р = 0,98 близка к 1, можно говорить о высокой степени вероятности того, что экспериментальные данные соответствуют нормальному закону.

---

Упражнение 1.

Проверить гипотезу о нормальном распределении случайной величины, распределение которой задано таблицей:

i	1	2	3	4	5	6	7	8
xi	-2	2	6	10	14	18	22	26
xi+1	2	6	10	14	18	22	26	30
ni	5	10	14	20	18	12	6	5

Уровень значимости α=0,05.

Упражнение 2.

Проверить гипотезу о нормальном распределении случайной величины по заданному интервальному распределению выборки объемом n = 200 на уровне значимости 0,02.

№ интервала i	Границы интервала		Частота ni	№ интервала	Границы интервала		Частота ni
	xi	xi+1			xi	xi+1
1	6	8	15	6	16	18	26
2	8	10	19	7	18	20	20
3	10	12	25	8	20	22	20
4	12	14	30	9	22	24	13
5	14	16	28	10	24	26	4

Упражнение 3.

В одном из вузов выборочно у 110 юношей измерили рост, данные помещены в таблице.

i	1	2	3	4	5	6	7	8	9
xi	156	160	164	168	172	176	180	184	188
xi+ 1	160	164	168	172	176	180	184	188	192
ni	1	2	6	20	33	25	15	5	3

На уровне значимости α=0,02 проверить гипотезу о нормальном распределении роста юношей в данном вузе.

Упражнение 4.

Произвольно выбранным 100 телезрителям предложили высказать свое отношение к рекламе согласно 12-ти балльной оценке. Результат представлен в таблице.

Балл	0-2	2-4	4-6	6-8	8-10	10-12
Число телезрителей	4	14	30	28	16	8

Проверить гипотезу о нормальном распределении оценки рекламы. При каком α проходит данная гипотеза?

Упражнение 5.

Для контроля успеваемости в данном вузе случайным образом были выбраны 100 студентов, для каждого из которых был сосчитан средний балл по итогам сессии. Результат показан в таблице.

Средний балл	2,7-3,1	3,1-3,5	3,5-4,0	4,0-4,5	4,5-5,0
Количество студентов с этим баллом	15	17	30	18	20

Проверить гипотезу о нормальном распределении среднего балла в данном вузе. При каком α данная гипотеза принимается?

---

Смотрите также файлы

• ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6.doc

• Metod_ukaz_190600.doc

• Методичка ПСТС.doc

• extrimism_pamyatka_studentam.doc

• Методичка MS Excel(2011).doc