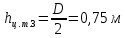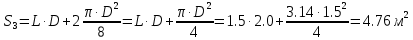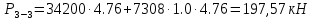ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 340
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЗАДАЧА 1
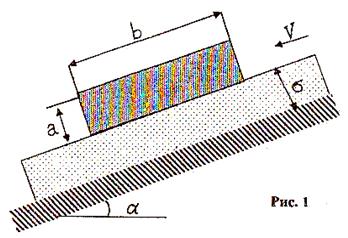
Определить (рис.1) скорость
Исходные данные к задаче: масло АМГ-10; а = 470 мм; b = 290 мм; с = 20 мм; σ = 0,4 мм;
Решение
По формуле Ньютона:
Пластина скользит под воздействием силы F, обусловленной силой тяжести и направленной параллельно плоскости пластины, которая может быть выражена в виде:
где
Коэффициент динамической вязкости
Так как толщина слоя масла мала, можно считать, что скорости частиц жидкости в нем изменяются по прямолинейному закону. Следовательно, градиент скорости можно выразить как
При равномерном движении пластины работа, совершаемая силой F, расходуется на преодоление работы сил вязкого трения Т, т.е.
поэтому по абсолютной величине эти силы будут равны.
или
Выражаем скорость скольжения пластины:
Скорость равномерного скольжения прямоугольной пластины
Задача 2.Зазор А между валом и втулкой заполнен маслом (рисунок а). Длина втулки L. К валу, диаметр которого D, приложен вращающий момент М. При вращении вала масло постепенно нагревается и скорость вращения увеличивается. Определить частоту вращения вала при температуре масла 27ºС.(Таблица 1).
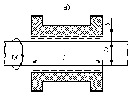
Таблица 1
| M, Н·м | 18,00 |
| δ, мм | 2,4 |
| D, мм | 350 |
| l, мм | 1000 |
| жидкость | Индустриальное 30 |
| | |
Запишем формулу Ньютона:
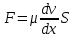 (1)
(1)где F – сила трения; – динамическая вязкость масла; S – площадь соприкосновения твердой поверхности с жидкостью; dv/dx – градиент скорости.
Площадь соприкосновения вала с жидкостью определим по формуле:
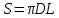 (1)
(1)Динамическую вязкость жидкости определяем по формуле:
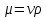 (1)
(1)где ν – кинематическая вязкость масла; ρ – плотность масла.
Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону.
Тогда формула приобретает вид:
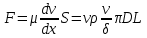 (1)
(1)Силу трения определяем из формулы момента:
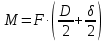 (1)
(1) Из-за малости зазора вторым членом δ/2 в скобках можно пренебречь.
При малом зазоре, когда
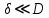 , кривизной слоя жидкости пренебрегаем, рассматривая ее движение в зазоре как плоскопараллельное. Считая, что скорости v в слое масла изменяются по прямолинейному закону, эпюра касательных напряжений τ имеет вид прямоугольника. Следовательно, сила трения F проходит через центр тяжести этой эпюры, т. е. посередине слоя масла.
, кривизной слоя жидкости пренебрегаем, рассматривая ее движение в зазоре как плоскопараллельное. Считая, что скорости v в слое масла изменяются по прямолинейному закону, эпюра касательных напряжений τ имеет вид прямоугольника. Следовательно, сила трения F проходит через центр тяжести этой эпюры, т. е. посередине слоя масла.Частоту n вращения вала и угловую скорость ω определяем при помощи известных формул:
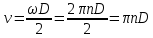 (2)
(2)Выведем формулу для определения частоты n вращения вала:
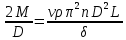 (2)
(2)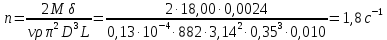
Задача 3 На рис. 1 представлено начальное положение гидравлической системы дистанционного управления (рабочая жидкость между поршнями не сжата). При перемещении ведущего поршня (его диаметр D) вправо жидкость постепенно сжимается и давление в ней повышается. Когда манометрическое давление рм достигает определенной величины, сила давления на ведомый поршень (его диаметр d) становится больше силы сопротивления F, приложенной к штоку ведомого поршня. С этого момента приходит в движение вправо и ведомый поршень. Диаметр соединительной части цилиндров δ, длина l(см. табл.1).
Требуется определить диаметр ведущего поршня D, необходимый для того, чтобы при заданной величине силы F ход L обоих поршней был один и тот же.
Коэффициент объемного сжатия рабочей жидкости принять βW= 0,0005 1/МПа.
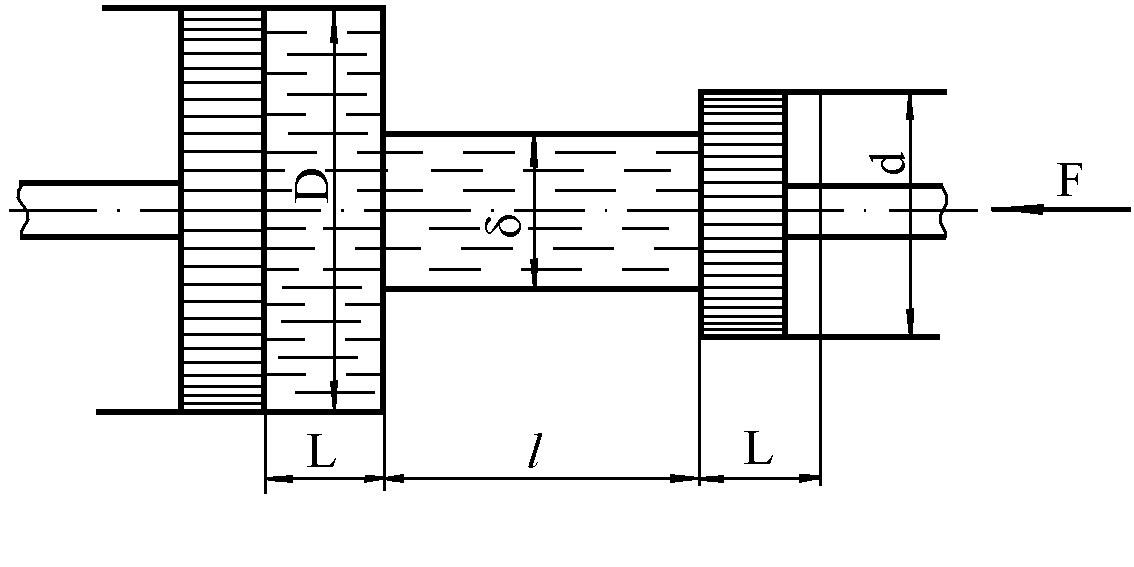
Рис.1
Таблица 1
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| d, мм L, мм δ, мм l, м F, кН | 40 60 20 5 30,2 | 36 50 16 2,2 23,7 | 48 64 24 2 34,6 | 56 72 28 2,4 67,9 | 40 80 20 3,8 19,8 | 50 40 34 2 33,9 | 60 72 40 2,3 50,8 | 52 54 22 2,5 35,5 | 45 50 30 2,5 31,8 | 25 34 10 1,75 13 |
Решение
Определяем манометрическое давление рм, при котором начнется движение ведомого поршня.
рм =
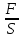 =
=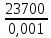 = 237000000 Па = 237 МПа
= 237000000 Па = 237 МПаS=
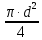 =
= 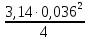 = 0,001
= 0,001 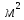
На основании заданного условия должно выполняться равенство:
 .
.С другой стороны, на основании формулы коэффициента объемного сжатия:
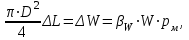
где W – первоначальный (исходный) объем гидравлической системы дистанционного управления.
W =
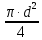
 L +
L + 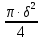
 l
lИспользуя эти уравнения, следует найти искомую величину необходимого диаметра ведущего поршня D.
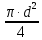
 L - βW
L - βW 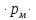 (
(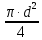
 L +
L + 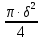
 l)=
l)=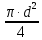
 L
LD2=
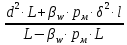
D=
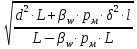 =
= 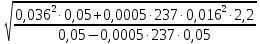 = 0,05 м = 50мм
= 0,05 м = 50ммОтвет: D=50мм
Задача 4
Горизонтальный цилиндрический резервуар, закрытый полусферическими днищами, заполнен жидкостью Ж (рисунок 2).
Длина цилиндрической части резервуара L, диаметр D. Манометр показывает манометрическое давление
рМ. Температура жидкости 200 С. Определить силы, разрывающие резервуар по сечениям 1-1, 2-2, 3-3.(таблица 2)

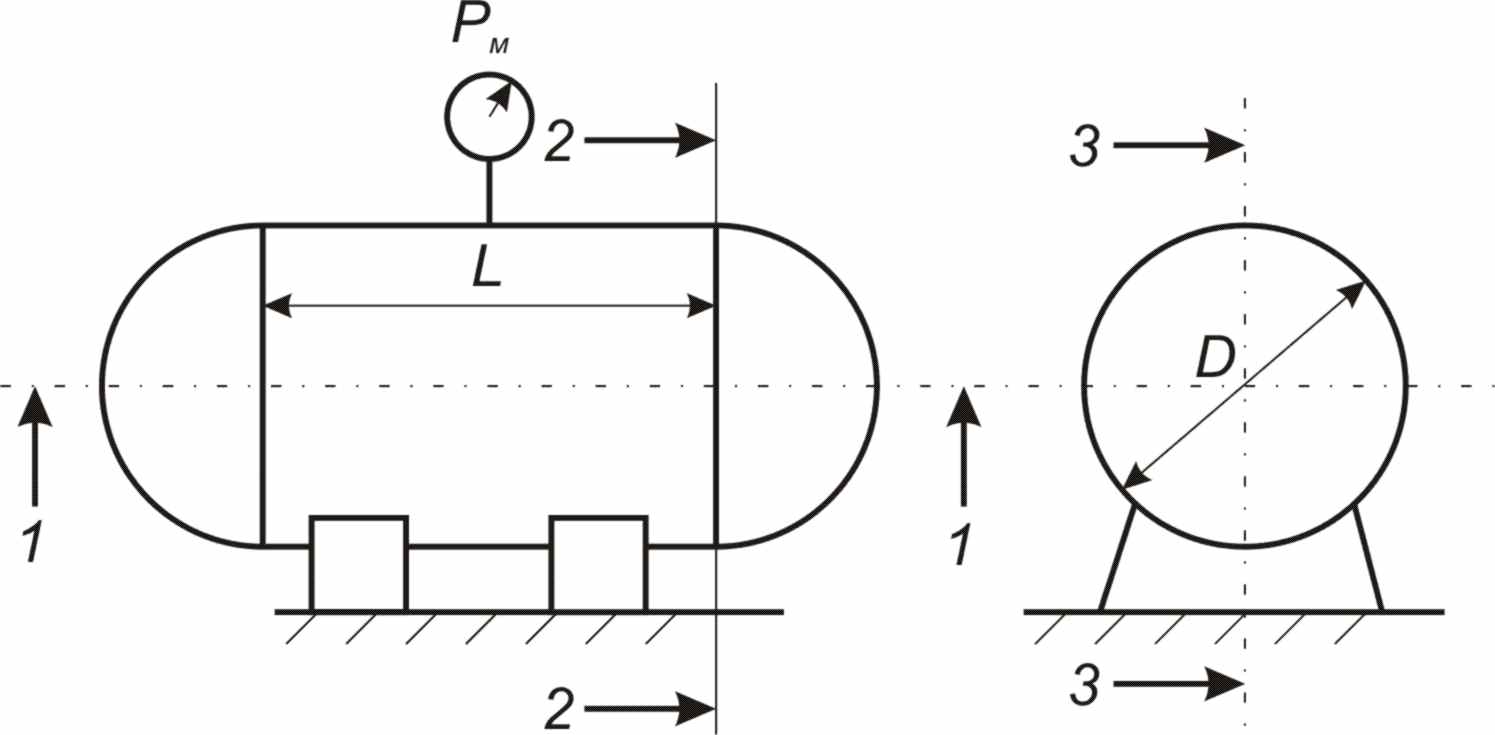
Рисунок 2
Таблица 2
| Жидкость | D, м | L, м | рМ, кПа |
| Нефть,Баку,тяжелая | 1.5 | 2.0 | 34.2 |
Решение:
Из основного уравнения гидростатики и учитывая вертикальную составляющую силу давления, направленную противоположно (вниз):
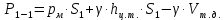 (3)
(3)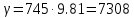 – удельный вес нефти при температуре 200 С, Н/м3;
– удельный вес нефти при температуре 200 С, Н/м3;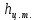 – высота центра тяжести, м;
– высота центра тяжести, м; 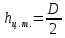
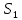 - площадь сечения цистерны в сечении 1-1, м2,
- площадь сечения цистерны в сечении 1-1, м2,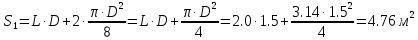
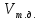 - объем тела давления, м3
- объем тела давления, м3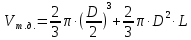 (3)
(3)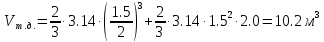
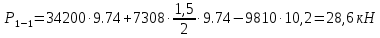
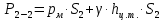 (3)
(3)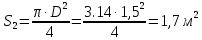
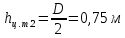
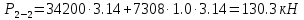
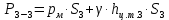 (3)
(3)