Файл: Поверхностный эффект. Волны на поверхности раздела двух диэлектрических сред.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН
САМАРКАНДСКИЙ ФИЛИАЛ ТАШКЕНТСКОГО УНИВЕРСИТЕТА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ИМЕНИ МУХАММАДА АЛ-ХОРАЗМИЙ
ФАКУЛЬТЕТ:
«ТЕЛЕКОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ И ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ»
Самостоятельная работа №1
по предмету: Электромагнитные поля и волны
ТЕМА: Поверхностный эффект. Волны на поверхности раздела двух диэлектрических сред.
Выполнил(а): Файзуллаев Ф. С
Проверил(а): Егамов Ш. В
САМАРКАНД – 2023
Поверхностные волны – это волны, которые распространяются вдоль границы раздела двух сред и приникают в эти среды на расстояние, меньшее длины волны. В поверхностных волнах вся энергия сосредоточена в узкой окрестности границы раздела, и состояние поверхности существенно влияет на их распространения. Именно поэтому поверхностные волны являются источником информации о состоянии поверхности. Более того, взаимодействие объемных и поверхностных волн может приводить к различным поверхностным эффектам, таким как генерация гармоник, вращение плоскости поляризации при отражении и так далее.
Волны такого типа возникают при падении объемной волны из диэлектрика на поверхность металла что обуславливается некоторыми особеностями распространения волн в средах со своободными зарядами,примерами которых являются металлы. При падении волны на такое вещество,свободные электроны колеблются под действием внешнего переменного поля волны. Ионы также испытывают действие поля,но поскольку их масса относительно велика,то в первом приблиении их считают неподвижными.
Уравнение движения для электронов имеет вид:
mr'' + mr' = еЕ
Здесь Е — среднее макроскопическое поле; в отличие от диэлектриков при изучении плазмы можно считать, что действующее поле примерно равно макроскопическому; v — эффективная частота соударений электронов с ионами и нейтральными
молекулами.
Учитывая,что поле Е волны переменно: Е ехр (—i t) ;
r'=eE/m(-i ); Поляризация будет равна:
j = eNr = DР/dt = —iР, P = i*(e^2NE/m(-i));
ε=1 — p^2/(^2+^2)+ i*p^2()/(^2-^2);
Мнимая часть диэлектрической проницаемости есть проводимость среды, то есть внешнее,даже переменное поле проникает в металл на расстояния порядка длины волны,за счет того что электрон,двигаясь в нем,создают аналогичное поле(экранируют внешнее). При p электоны не «успевают» за полем,и металл становится прозрачным.
Также стоит отметить,что плазмонные волны являются ТМ-волнами,в которых вектор поляризации перпендикулярен плоскости падения.
Действительно,если бы в рассматриваемой волне имелась компонента,параллельная плоскости падения,то она вынуждала бы электроны в тонком пограничном слое колебаться туда-обратно через поверхность металла. Но электроны не могут уйти с поверхности раздела из-за потенциального барьера,то есть энергия данной компоненты поляризации гаснет на поверхностном энергетическом барьере.
Для возбуждения поверхностных волн необходимо условие фазоаго синхронизма возбуждаемой волны с возбуждающей. Другими словами, если в кристаллической структуре имеет место
согласование фаз, то величина выходного сигнала будет значи- значительной; если же согласование фаз отсутствует, то можно полу- получить лишь весьма слабый сигнал.
Возникает вопрос, что происходит с энергией в случае отсут- отсутствия согласования фаз в структуре? Или, точнее, что происхо- происходит с частью энергии, которая расходуется на генерацию тех
частотных компонент нелинейной поляризации, для которых отсутствует согласование фаз? Этот вопрос важен, поскольку такие частотные компоненты всегда существуют. Если
бы эта энергия терялась (например, вследствие поглощения), то любой нелинейный оптический процесс всегда сопровождался бы сильным затуханием.
Ответ на этот вопрос заключен в фазе сигнала. Пренебрегая тензорной природой ε, напишем формулу плотности потока энергии:
DP/dt= (1/4)[ε*Dε/dt+H*DH/dt]+ε*Dp/dt
Член в скобках в правой части уравнения есть скорость возрастания энергии электромагнитной волны в вакууме; по- последний член — энергия, затраченная на изменение электриче- электрической поляризации. Энергия поляризации равна
W=*Dp/dt;
усредненная по периоду, большому по
сравнению с 2. Таким образом, средняя поглощенная энергия равна
W=1/2Psin разность фаз между волной поляризации и электро- магнитной волной. При генерируемый сигнал отстает от падающей волны на 90 градусов-это означает,что энергия W отрицательна,т.е энергия переходит от волны поляризации к электромагнитной волне,но при ≠ это вообще не верно.При дальнейшем распространении волны поток энерги меняет знак-вместо перехода энергии от электромагнитной волны к волне поляризации происходит обратный процесс.Иначе говоря,энергия генерируемой волны возвращается исходному излучению.
Методы возбуждения ПЭВ
Хотя ПЭВ является собственной модой плоской границы раздела, для ее возбуждения светом нужны специальные условия, поскольку волновой вектор ПЭВ Sk больше волнового вектора света k0 на той же частоте. К настоящему времени разработаны два эффективных метода возбуждения ПЭВ светом (рис. 2): призменный и решеточный.
Призменный метод возбуждения ПЭВ
Преобразование света в ПЭВ призменным методом основано на явлении нарушенного полного внутреннего отражения при падении p-поляризованного излучения (поляризованного в плоскости падения) на ПАС со стороны оптиче- ски более плотной среды. Угол падения θ выбирается из известного в оптике условия
θ arcsin(sqrt(ε1 ε3 , ε1 ε3
где ε3 – диэлектрическая проницаемость материала призмы. Метод существует в двух модификациях: геометрия Отто (рис. 1 а) и геометрия Кречманна (рис.1б). Этим методом ПЭВ возбуждается на гладкой поверхности, поскольку притрансформации объемного излучения в ПЭВ удается согласовать их волновые векторы. В большинстве случаев источниками света в соответствующих устройствах генерации ПЭВ являются лазеры.
Эффективность преобразования падающего объемного излучения в ПЭВ в схеме Отто, чаще применимой для ИК-области спектра (СО2-лазеры), достигает десятых долей, а в геометрии Кречманна для видимого света практически доходит до 1. Однако в последнем слу-чае вывод ПЭВ за пределы призмы
затруднен, и ПАС обычно наносится на еегрань в виде тонкой пленки. Обратное преобразование ПЭВ в объемное излучение также возможно с помощью призм.
Двупризменный метод возбуждения и детектирования ПЭВ в геометрии
Отто успешно используется в ИК-спектроскопии твердого тела. Длина пробега ПЭВ вдоль поверхности может достигать нескольких сантиметров, она весьма чувствительна к процессам в поглощающем слое, состоянию поверхности и его изменениям, наличию адсорбированных слоев, пленок, шероховатости и др.
Это обеспечивает возможность исследовать поверхности и границы раздела с помощью ПЭВ, а также осуществлять прецизионные оптические измерения, на- пример измерять малое поглощение высоко отражающих металлических зеркал на уровне 0,01 с ошибкой не более до 10%..
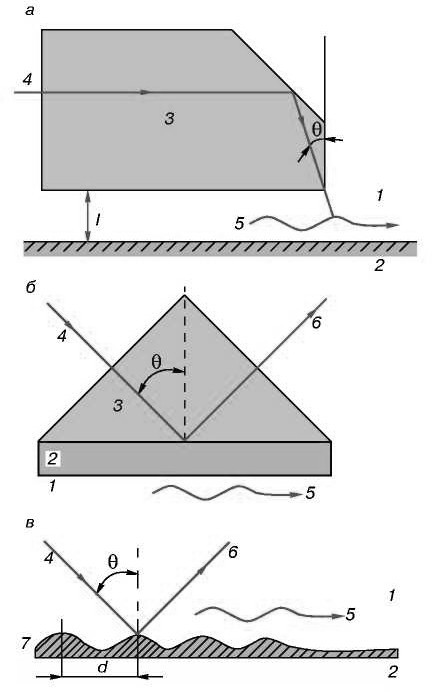
Рис.1 Возбуждение ПЭВ светом: а - призменный метод, геометрия Отто; б - призменный метод, геометрия Кречманна; в - решеточный метод. 1 - диэлектрик
( воздух); 2 - поверхностно-активная среда; 3 - призма; 4 - падающее излучение; 5 - ПЭВ; 6 - зеркально отраженное излучение; 7 - решетка; l - зазор размером
λ; d- период решетки.
Возбуждение ПЭВ на решетке
Свойством возбуждать ПЭВ обладают и дифракционные решетки, нане- сенные на поверхностно-активную среду (рис. 1 в) и рассеивающие излучение
под определенными углами. Когда при некоторых углах падения света θди- фрагированная волна оказывается направленной вдоль поверхности, она пред- ставляет собой ПЭВ. Волновой вектор g⃗ решетки с периодом dнаправленный перпендикулярно ее штрихам и по модулю равеный 2π d(резонансная, гармо- ническая решетка) связан с волновым вектором ПЭВ kS
и векторной проекцией ktволнового вектора излучения k0
на поверхность (рис. 2 а) равенством
kt+ mg=KS
m1,2,...; kt k0*sinθ
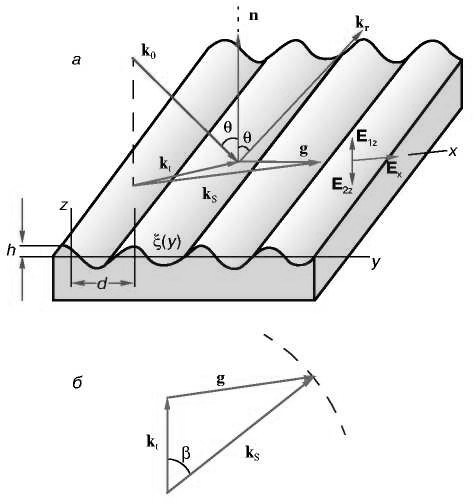Оно выражает закон сохранения импульса (иначе – условие фазового синхро- низма) при преобразовании света в поверхностные поляритоны без изменения частоты. В выражении m–порядок дифракции, который будем считать равным единице. Взаимную ориентацию векторов kS,k tи g⃗ удобно поясняет круговая векторная диаграмма (рис. 2б).
Рис. 2. Взаимная ориентация (а) и круговая диаграмма (б) векторов,
определяющих преобразование света в ПЭВ на гармонической решетке ξ ( y) h cos(gy) с амплитудой h , пространственной частотой g и периодом d 2πg.k t- проекция волнового вектора k0 на плоскость поверхности; ks-волновой вектор ПЭВ; krволновой вектор отраженного излучения; g⃗-волновой вектор решетки;n⃗- нормаль к усредненной поверхности; θ- угол падения света.
Штриховкой очерчена часть окружности радиуса Skна круговой диаграмме.
Из количественной теории преобразования света в ПЭВ на периодиче- ских решетках следует, что для излучений p-и s-поляризаций продольный
компонент поля ПЭВ на поверхности Exи действующее внешнее поле Etпро- порциональны, а соответствующий коэффициент пропорциональности в пер- вом приближении линейно зависит от высоты h резонансной гармонической решетки. Для случая нормального падения излучения эта связь наиболее про- ста:
Ex μEh
Параметр μ, называется коэффициентом преобразования и является ком- плексной величиной, зависящей от волнового числа поверхностного полярито- на kS . Модуль этого параметра μ , рассматриваемый как функция kS,фактиче-
ски описывает форму линии возбуждения поверхностного поляритона коге- рентным излучением при нормальном падении на резонансную решетку
(g kS). Ее типичный вид для поверхностного плазмон-поляритона на границе
металл-воздух показан на рис. 28. Центр линии kS0 kSпрактически совпадает с волновым числом "идеального" возбуждения, определяемым соотношением ks k0*sqrt(εεεε, а значение μв максимуме линии M и ее ширина Δопределяются диссипативными потерями в скин-слое металла. При этом
M=2*
=L/sqrt(2);
Для определенности отметим, что первая из формул (5.16) справедлива только для ближней ИК-области спектра. Если принять, например, что ПЭВ возбуждается на длине волны 1 мкм при нормальном падении света на резо- нансную решетку, то, как это следует из (5.16),
Δ≈50–200 см-1, M
107 см-1
Отсюда следует, что поляритонная линия достаточно узкая, а продольное электрическое поле ПЭВ x E сравнивается с полным полем на поверхности t Eпри высоте резонансной решетки всего лишь h
10−3λ
10-7–10-6 см (!)
На решетках большей высоты поле ПЭВ может превысить возбуждающее световое поле в десятки раз, что не противоречит никаким законам сохранения. Эти результаты, оказавшиеся неожиданными для оптики, свидетельст-
вуют о реальной возможности значительного электродинамического усиления светового поля на поверхности с резонансной решеткой, хотя преобразование в ПЭВ — чисто линейный по полю процесс, не зависящий от интенсивности све- та. Такое усиление является следствием, с одной стороны, сфазированной под- качки энергии объемной волны в ПЭВ при ее распространении вдоль резо- нансной решетки (отсюда видна важная роль когерентности падающего излуче- ния), а с другой — высокой локализации энергии в ПЭВ. Эффект усиления поля при возбуждении светом ПЭВ позволяет объяснить многие неясные ранее фо- тофизические явления на поверхности, протекающие в поле лазерного излуче- ния. Наконец все перечисленное показывает высокую энергетическую эффек- тивность дифракционного способа возбуждения ПЭВ светом с помощью резонансных решеток.
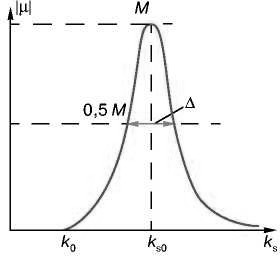
Рис. 3 Зависимость модуля коэффициента преобразования μизлучения в ПЭВ от волнового числа возбуждения Skпри условии нормального падения излучения на решетку с пространственной частотой Sg k.
Интерференционные эффекты с поверхностнымиплазмонами
В 2003 году Тако Фиссер (Свободный Университет Амстердама) теорети- чески рассмотрел намного более простую систему, состоящую всего лишь из двух узких параллельных щелей в металлической пленке, расположен- ных на некотором расстоянии другот друга (см. Рис.4а). В зависимости
от поляризации падающего излучения смоделированный спектр пропуска- ния такой системы состоял либо из периодических равноотстоящих мак- симумов, либо не имел ярко выраженных особенностей (см. Рис.4b). Фис- сер связал это с наличием поверхностных плазмонов, распространявшихся между щелями и интерферировавших со светом, напрямую распростра- нявшимся через них.
Важно отметить, что система двух щелей в непрозрачном экране явля- ется канонической системой физики. Она послужила английскому физику Томасу Юнгу для доказательства волновой природы света, а так же сыг- рала важную роль в понимании многих аспектов квантовой механики при изучении интерференции электронов, атомов и молекул.
С точки зрения физики поверхностных плазмонов привлекательностью данной системы является то, что каждая щель является как источником, так и приемником поверхностных плазмонов (Рис.3б). Более того, так как длина щели предполагается много больше длины волны падающего света, то щель представляет собой антенну, переизлучающую падающую на нее световую волну в направленную волну поверхностных плазмонов, распро- страняющуюся перпендикулярно щели по поверхности металла (Рис.4а).
Это дает возможность расположить вторую щель-приемник на достаточ-
но большом расстоянии от щели-источника, что позволяет поверхностным плазмонам распространяться по плоской, невозмущенной поверхности ме- таллической пленки, где свойства поверхностного плазмона могут быть описаны в простой аналитической форме.
Экспериментальные образцы, состояли из золотых и серебряных пленок толщиной 200 нм, напыленных настеклянные подложки, размерами × × .мм. Толщина пленки выбиралась таким образом, чтобы с одной стороны быть много больше глубины скин-слоя (глубины проникновения поля в металл), а с другой стороны быть меньше половины длины волны возбуждающего света, чтобыисключить резонансный характер пропускания щели. Резонансы в пропускании возникают из-за того, что щель в достаточно толстой пленке (больше половины длины волны) может вести себя как резонатор Фабри-Перо: световая мода, распространяющаяся внутри нее испытывает множествен-
ные отражения на границе щель-воздух, эти отражения интерферируют между собой, и спектр пропускания щели становится резонансным. Отра-
жения происходят из-за того, что значение постоянной распространения моды внутри щели превосходит показатель преломления воздуха, равный единице.
Критерием выбора золота и серебра, как основных металлов для про- изводства пленок, служило то, что ПП на данных металлах обладают в ви- димом оптическом диапазоне сравнительно небольшим затуханием и рас- пространяются на расстояния до сотни микрон. Преимуществом золота является то, что оно не окисляется на воздухе, поэтому удобно рассмат- ривать ПП на границе раздела золото-воздух. Преимуществом серебра, в отличие от золота, является отсутствие поглощения в сине-зеленой обла- сти видимого спектра, что позволяет наблюдать “синие” ПП, поле кото- рых сосредоточено больше в металле, чем в диэлектрике, и поэтому они обладают большой дисперсией и затуханием. Такие плазмоны представля- ют интерес для интегрированных нано-цепей, где необходима сверхмалая длина волны ПП.
С помощью сфокусированного пучка ионов галлия в золотых и серебря- ных пленках были изготовлены двущелевые системы различных размеров.Длина щелей составляла 50 мкм, ширина каждой щели составляла
100–200 нм, а расстояние между щелями изменялось от нескольких микрон до десятков микрон.
Рис. 4. Изображение поверхности экспериментального образца со щелями, полученное с помощью электронного сканирующего мик- роскопа.
Преобразование падающего света в плазмон напрямую
зависело от ширины щели, и было наиболее оптимальным, когда ширина щели составляла около четверти длины волны падающего света, то есть около 200 нм.
Расстояние между щелями выбиралось таким образом, чтобы оно с од- ной стороны было: а) много больше, чем длина волны падающего света, для исключения влияния щели на характер распространения ПП по глад- кой металлической поверхности, и б) было меньше, чем длина затухания ПП. К примеру, длина затухания ПП с длиной волны 800 нм, распростра- няющего по границе раздела воздух-золото, составляет около 100 мкм. На этой длине напряженность поля ПП падает в e.раз.
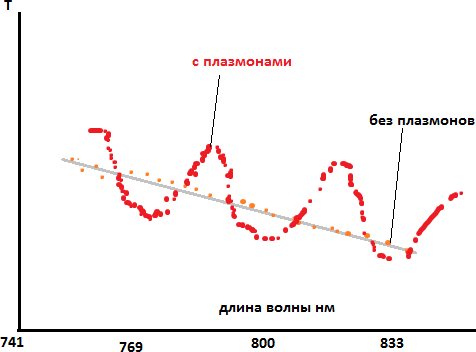
Идеей первого эксперимента была проверка существования ПП
в двущелевой системе. В качестве источника света использовался титан- сапфировый лазер с возможностью перестройки длины волны в неболь- шом диапазоне 740–830 нм. Пучок диаметром около 1 мм равномерно освещал исследуемую двущелевую систему в экспериментальном образце и свет, прошедший через щели собирался системой линз на фотодиодный детектор . Сигнал детектора записывался регистрационной систе-
мой как функция длины волны падающего света.
Полученные спектры пропускания двущелевых систем пред-
ставляли гармонические (почти синусоидальные) зависимости, хорошо со- гласующиеся с теоретическими расчетами Т. Фиссера. Для доказатель- ства того, что такая модуляция спектра пропускания была вызвана имен- но плазмонами, были проделаны дополнительные эксперименты. В пер- вом из них поляризация падающего на щели света, то есть направление электрического вектора, была выбрана параллельно щелям, в отличие от основного эксперимента, где она была перпендикулярна щелям. Для такой поляризации не должно было происходить возбуждения ПП. Действитель- но, спектр пропускания в этом случае не содержал никаких выраженных особенностей и слабо зависел от длины волны (см. Рис.4б). Аналогичный спектр для обеих поляризаций падающего света наблюдался и в случае, когда исследовалось пропускание сквозь щели, изготовленные в титано- вой пленке. Титан хотя и поддерживает ПП в рассматриваемом диапазоне длин волн, но длина затухания ПП составляет меньше одного микрона, то есть много меньше расстояния между щелями, и влияние ПП сводится к нулю.
Измеренные спектры пропускания хорошо описывались простой моделью,обьясняющую интерференцию между прошедшим светом и плазмоном,сгенерированным другой щелью. Фаза данного плазмона зависела от длины волны падающего света,и как следствие для определенных длин волн наблюдался максимум\минимум в спектре пропускания( это зависело от того,в фазе плазмон с первичным светом или нет).
Любопытно,что при освещении 1 щели светом лазера наблюдалась четкая интерференционная картина.Суть эффекта заключается в том, что плазмон, распространяющийся от освещеннойщели, доставляет часть световой энергии “темной щели” без потери фазы. Темная щель переизлучает этот плазмон на выходной стороне. Такимобразом, пучок каждого лазера расщепляется на два источника света: первый, определяемый прямым пропусканием через щель- источник и второй― плазмонный, излучаемый щелью-приемником. Так как процесс рассеяния света в плазмон и обратно происходит с сохранением фазы света,то эти два источника могут давать интерференционную картинку, что и наблюдается в эксперименте.Таким образом, если осветить только одну
щель, то на выходе будет наблюдаться интерференционная картина. Ко- гда же освещены две щели, на экране наблюдаются две наложенные друг на друга интерференционные картины. Их поля взаимно-некогерентны и поэтому происходит сложение интенсивностей, а не амплитуд, этих полей.
В другом эксперименте изучаемая система состоит из двух параллельных щелей, пересеченных третьей. Длина щелей составляет 100 мкм, расстояние между ними 10 мкм и наклонная щель пересекает их под углом около 10 градусов (Рис.10). Наклонная щель используется в данном эксперименте как сенсор для стоячей волны, образованной поверхностными плазмона- ми, распространяющимися другнавстречу друга от параллельных щелей- источников. Подобная стоячая волна образуется и в классическом опти- ческом резонаторе.С целью объяснения первоначально полученных экспериментальных
данных был проделан эксперимент Главы 6, в котором исследовалась сту- пенчатая щель, ширина элементов которой изменялась от 50 до 500 нм,
а длина составляла 10 мкм. Анализ интенсивности и поляризации све- та, прошедшего через нее показал, что действительно при ширине щели порядка 250 нм ТМ и ТЕ поля обладают одинаковыми коэффициентами
пропускания и их фазовая задержка составляет около π/. Для б´oльших ширин щели разность между пропусканием ТЕ и ТМ полей становилась неразличимой, а для меньших ширин затухание ТЕ волны значительно увеличивалось.
Теоретическое объяснение данного эффекта, подтвержденное модели- рованием, состояло в том, что глубина щели-волновода, или другими сло- вами, толщина золотой пленки, в которой была проделана щель, составля- ла 200 нанометров, то есть четверть длины волны падающего излучения. Это имело двойное влияние на ТМ/ТЕ пропускание. Во-первых, затуха- ние ТЕ волны было небольшим ― волна не успевала испытать значитель- ное затухание на такой небольшой длине волновода. При выходе из щели эта волна снова превращалась в свободно распространяющийся свет. Фаза ТЕ волны при таком распространении не меняется, ввиду ее затухающе- го характера. Во-вторых, ТМ волна может распространяться через щель- волновод и ее фаза увеличивается как раз на π. Если бы толщина золо- той пленки была бы, например, равна 400 нм, это значение составило бы π. Таким образом, щель являлась дихроическим двулучепреломляющим устройством: в ней могли распространяться две волны с ортогональными
поляризациями и различным затуханием. Фазы и амплитуды волн, про- шедших через щель, зависели от ее ширины и глубины (толщины пленки). Подбирая параметры щели можно было варьировать поляризацию поля, которое проходит через нее.
Микроскоп на плазмонах.
Это микоскопы,обладающие высокой разрешающей способностью. Как известно из квантовой физики,частица занимает в пространстве так называемую фазовую ячейку,размеры которой есть неопределенность положения и импульса в пространстве. Строго говоря,если нам известна одна координата с высокой степенью точности,вторая координата фактически неопределена. Если представить фазовую ячейку пространства как кубик,то возможно,не изменяя обьема,трансформировать его в тонкую пластину и
«пустить» по ней частицу-квант.Точность определения направления движения кванта в плоскости, параллельной плоскости плстины, напрямую связана с её толщиной. Иначе говоря, чем в более тонкий блин раскатаем наш объем, тем с большей точностью мы сможем измерять направление движения кванта в плоскости. Итак, мы, оказывается, можем точно определять одну из проекций радиус-вектора и одну из проекций импульса. Только эти проекции взаимно перпендикулярны .Плазмоны и есть те частицы,локализованные в тонком слое. В основу конструкции поверхностно-плазмонного микроскопа положена схема возбуждения поверхностных плазмонов по методу Кречманна. На гипотенузную грань прямоугольной треугольной призмы наносится тонкая металлическая пленка. Ее освещают со стороны призмы монохроматическим линейно поляризованным светом с расходимостью на порядок меньше, чем полуширина резонансной кривой для данной пленки. Причем вектор поляризации лежит в плоскости падения света — так называемый Р- поляризованный свет. Отраженный от пленки свет попадает на фотоматрицу, сигнал с которой обрабатывается компьютером. Мы помним, что разрешение в плоскости пленки у нас несколько микрон. Поэтому между призмой и фотоматрицей на пути света ставится телескоп, расширяющий пучок так, чтобы свет, идущий с микронной площадки пленки, захватывал несколько элементов фотоматрицы.
Условия резонансного возбуждения ПП зависят не только от свойств металлической пленки, на поверхности которой они возбуждаются, но и от диэлектрических свойств среды, с которой эта пленка граничит. Любую тонкую пленку на поверхности металла можно представить как локальное изменение диэлектрических свойств внешней среды. А это сразу сказывается на условии резонансного возбуждения в этом месте ПП. Иначе говоря, резонансная кривая смещается в этом месте относительно кривой для чистой пленки в область больших углов.
Значит, если настроить наш микроскоп на угол, соответствующий оптимальному возбуждению ПП для чистой металлической пленки, то в тех местах, где будет находиться измеряемый объект, интенсивность отраженного света будет больше, и тем больше, чем толще этот фрагмент.
На самом деле ясно, что микроскоп реагирует не на толщину, а на изменения параметра ed, где - диэлектрическая проницаемость, d - толщина измеряемого объекта.
Разрешение микроскопа будет тем лучше, чем на большее расстояние сумеет распространиться ПП. Это зависит,во-первых,от гладкости поверхности,а во- вторых,от мнимой части диэлектрической проницаемости материала пленки. Наиболее подходящее в этом отношении серебро-длина плазмонов составляет примерно 100 микрон.
Суммируя сказанное,отметим,что плазмон-поляритонные волны есть связанное колебание вектора Е и электронов с тонком пограничном слое металла,обладающего при условиях возбуждения отрицательной диэлектрической проницаемостью. Поляризация волн-толькоТМ,волновой вектор больше вектора порождающего излучения,но существует уменьшение интенсивности. Длина,затухание и энергия данных волн очень сильно зависят от вида и гладкости поверхности. То есть чтобы управлять свойствами поверхностной волны или же реализовывать какие-то особые необходимые свойства,необходимо подобрать соответствующий образец-из определенного вещества и с определенной поверхностью. Щели на образце являются резонаторами для плазмонов,они преобразуют свет в плазмоны,а плазмоны в свет,то есть при освещении лишь 1 щели на второй также будут возникать возмущения,и она по принципу Гюйгенса-Френеля будет источником электро- магнитных волн.если же в образце есть 3-ья щель,то она играет роль волновода для стоячей волны. Со свойством сильной зависимости параметров волн от поверхности распространения связано применение плазмонов при детектировании микрообьектов.
Литература:
-
Виноградова,Руденко,Сухоруков. Теория волн, М.:Просвящение,1990 г.
-
Ф. Цернике, Дж. Мидвинтер,Прикладная нелинейная оптика М.: Мир, 1976 г.
-
N. V. Kuzmin, Interference Effects with Surface Plasmons. Leiden University, 2008 г.
-
М.Н. Либенсон, Е.Б. Яковлев, Г.Д. Шандыбина.Взаимодействие излучения с веществом (силовая оптика). Конспект лекций под редакцией Вейко В.П. СПб.: СПбГУ ИТМО, 2008
-
Волкова З.А. Поверхностные электромагнитные волны. М.:2005 г.
МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН
САМАРКАНДСКИЙ ФИЛИАЛ ТАШКЕНТСКОГО УНИВЕРСИТЕТА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ИМЕНИ МУХАММАДА АЛ-ХОРАЗМИЙ
ФАКУЛЬТЕТ:
«ТЕЛЕКОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ И ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ»
Самостоятельная работа №1
по предмету: Электромагнитные поля и волны
ТЕМА: Поверхностный эффект. Волны на поверхности раздела двух диэлектрических сред.
Выполнил(а): Файзуллаев Ф. С
Проверил(а): Егамов Ш. В
САМАРКАНД – 2023
Поверхностные волны – это волны, которые распространяются вдоль границы раздела двух сред и приникают в эти среды на расстояние, меньшее длины волны. В поверхностных волнах вся энергия сосредоточена в узкой окрестности границы раздела, и состояние поверхности существенно влияет на их распространения. Именно поэтому поверхностные волны являются источником информации о состоянии поверхности. Более того, взаимодействие объемных и поверхностных волн может приводить к различным поверхностным эффектам, таким как генерация гармоник, вращение плоскости поляризации при отражении и так далее.
Волны такого типа возникают при падении объемной волны из диэлектрика на поверхность металла что обуславливается некоторыми особеностями распространения волн в средах со своободными зарядами,примерами которых являются металлы. При падении волны на такое вещество,свободные электроны колеблются под действием внешнего переменного поля волны. Ионы также испытывают действие поля,но поскольку их масса относительно велика,то в первом приблиении их считают неподвижными.
Уравнение движения для электронов имеет вид:
mr'' + mr' = еЕ
Здесь Е — среднее макроскопическое поле; в отличие от диэлектриков при изучении плазмы можно считать, что действующее поле примерно равно макроскопическому; v — эффективная частота соударений электронов с ионами и нейтральными
молекулами.
Учитывая,что поле Е волны переменно: Е ехр (—i t) ;
r'=eE/m(-i ); Поляризация будет равна:
j = eNr = DР/dt = —iР, P = i*(e^2NE/m(-i));
ε=1 — p^2/(^2+^2)+ i*p^2()/(^2-^2);
Мнимая часть диэлектрической проницаемости есть проводимость среды, то есть внешнее,даже переменное поле проникает в металл на расстояния порядка длины волны,за счет того что электрон,двигаясь в нем,создают аналогичное поле(экранируют внешнее). При p электоны не «успевают» за полем,и металл становится прозрачным.
Также стоит отметить,что плазмонные волны являются ТМ-волнами,в которых вектор поляризации перпендикулярен плоскости падения.
Действительно,если бы в рассматриваемой волне имелась компонента,параллельная плоскости падения,то она вынуждала бы электроны в тонком пограничном слое колебаться туда-обратно через поверхность металла. Но электроны не могут уйти с поверхности раздела из-за потенциального барьера,то есть энергия данной компоненты поляризации гаснет на поверхностном энергетическом барьере.
Для возбуждения поверхностных волн необходимо условие фазоаго синхронизма возбуждаемой волны с возбуждающей. Другими словами, если в кристаллической структуре имеет место
согласование фаз, то величина выходного сигнала будет значи- значительной; если же согласование фаз отсутствует, то можно полу- получить лишь весьма слабый сигнал.
Возникает вопрос, что происходит с энергией в случае отсут- отсутствия согласования фаз в структуре? Или, точнее, что происхо- происходит с частью энергии, которая расходуется на генерацию тех
частотных компонент нелинейной поляризации, для которых отсутствует согласование фаз? Этот вопрос важен, поскольку такие частотные компоненты всегда существуют. Если
бы эта энергия терялась (например, вследствие поглощения), то любой нелинейный оптический процесс всегда сопровождался бы сильным затуханием.
Ответ на этот вопрос заключен в фазе сигнала. Пренебрегая тензорной природой ε, напишем формулу плотности потока энергии:
DP/dt= (1/4)[ε*Dε/dt+H*DH/dt]+ε*Dp/dt
Член в скобках в правой части уравнения есть скорость возрастания энергии электромагнитной волны в вакууме; по- последний член — энергия, затраченная на изменение электриче- электрической поляризации. Энергия поляризации равна
W=*Dp/dt;
усредненная по периоду, большому по
сравнению с 2. Таким образом, средняя поглощенная энергия равна
W=1/2Psin разность фаз между волной поляризации и электро- магнитной волной. При генерируемый сигнал отстает от падающей волны на 90 градусов-это означает,что энергия W отрицательна,т.е энергия переходит от волны поляризации к электромагнитной волне,но при ≠ это вообще не верно.При дальнейшем распространении волны поток энерги меняет знак-вместо перехода энергии от электромагнитной волны к волне поляризации происходит обратный процесс.Иначе говоря,энергия генерируемой волны возвращается исходному излучению.
Методы возбуждения ПЭВ
Хотя ПЭВ является собственной модой плоской границы раздела, для ее возбуждения светом нужны специальные условия, поскольку волновой вектор ПЭВ Sk больше волнового вектора света k0 на той же частоте. К настоящему времени разработаны два эффективных метода возбуждения ПЭВ светом (рис. 2): призменный и решеточный.
Призменный метод возбуждения ПЭВ
Преобразование света в ПЭВ призменным методом основано на явлении нарушенного полного внутреннего отражения при падении p-поляризованного излучения (поляризованного в плоскости падения) на ПАС со стороны оптиче- ски более плотной среды. Угол падения θ выбирается из известного в оптике условия
θ arcsin(sqrt(ε1 ε3 , ε1 ε3
где ε3 – диэлектрическая проницаемость материала призмы. Метод существует в двух модификациях: геометрия Отто (рис. 1 а) и геометрия Кречманна (рис.1б). Этим методом ПЭВ возбуждается на гладкой поверхности, поскольку притрансформации объемного излучения в ПЭВ удается согласовать их волновые векторы. В большинстве случаев источниками света в соответствующих устройствах генерации ПЭВ являются лазеры.
Эффективность преобразования падающего объемного излучения в ПЭВ в схеме Отто, чаще применимой для ИК-области спектра (СО2-лазеры), достигает десятых долей, а в геометрии Кречманна для видимого света практически доходит до 1. Однако в последнем слу-чае вывод ПЭВ за пределы призмы
затруднен, и ПАС обычно наносится на еегрань в виде тонкой пленки. Обратное преобразование ПЭВ в объемное излучение также возможно с помощью призм.
Двупризменный метод возбуждения и детектирования ПЭВ в геометрии
Отто успешно используется в ИК-спектроскопии твердого тела. Длина пробега ПЭВ вдоль поверхности может достигать нескольких сантиметров, она весьма чувствительна к процессам в поглощающем слое, состоянию поверхности и его изменениям, наличию адсорбированных слоев, пленок, шероховатости и др.
Это обеспечивает возможность исследовать поверхности и границы раздела с помощью ПЭВ, а также осуществлять прецизионные оптические измерения, на- пример измерять малое поглощение высоко отражающих металлических зеркал на уровне 0,01 с ошибкой не более до 10%..
Рис.1 Возбуждение ПЭВ светом: а - призменный метод, геометрия Отто; б - призменный метод, геометрия Кречманна; в - решеточный метод. 1 - диэлектрик
( воздух); 2 - поверхностно-активная среда; 3 - призма; 4 - падающее излучение; 5 - ПЭВ; 6 - зеркально отраженное излучение; 7 - решетка; l - зазор размером
λ; d- период решетки.
Возбуждение ПЭВ на решетке
Свойством возбуждать ПЭВ обладают и дифракционные решетки, нане- сенные на поверхностно-активную среду (рис. 1 в) и рассеивающие излучение
под определенными углами. Когда при некоторых углах падения света θди- фрагированная волна оказывается направленной вдоль поверхности, она пред- ставляет собой ПЭВ. Волновой вектор g⃗ решетки с периодом dнаправленный перпендикулярно ее штрихам и по модулю равеный 2π d(резонансная, гармо- ническая решетка) связан с волновым вектором ПЭВ kS
и векторной проекцией ktволнового вектора излучения k0
на поверхность (рис. 2 а) равенством
kt+ mg=KS
m1,2,...; kt k0*sinθ
Оно выражает закон сохранения импульса (иначе – условие фазового синхро- низма) при преобразовании света в поверхностные поляритоны без изменения частоты. В выражении m–порядок дифракции, который будем считать равным единице. Взаимную ориентацию векторов kS,k tи g⃗ удобно поясняет круговая векторная диаграмма (рис. 2б).
Рис. 2. Взаимная ориентация (а) и круговая диаграмма (б) векторов,
определяющих преобразование света в ПЭВ на гармонической решетке ξ ( y) h cos(gy) с амплитудой h , пространственной частотой g и периодом d 2πg.k t- проекция волнового вектора k0 на плоскость поверхности; ks-волновой вектор ПЭВ; krволновой вектор отраженного излучения; g⃗-волновой вектор решетки;n⃗- нормаль к усредненной поверхности; θ- угол падения света.
Штриховкой очерчена часть окружности радиуса Skна круговой диаграмме.
Из количественной теории преобразования света в ПЭВ на периодиче- ских решетках следует, что для излучений p-и s-поляризаций продольный
компонент поля ПЭВ на поверхности Exи действующее внешнее поле Etпро- порциональны, а соответствующий коэффициент пропорциональности в пер- вом приближении линейно зависит от высоты h резонансной гармонической решетки. Для случая нормального падения излучения эта связь наиболее про- ста:
Ex μEh
Параметр μ, называется коэффициентом преобразования и является ком- плексной величиной, зависящей от волнового числа поверхностного полярито- на kS . Модуль этого параметра μ , рассматриваемый как функция kS,фактиче-
ски описывает форму линии возбуждения поверхностного поляритона коге- рентным излучением при нормальном падении на резонансную решетку
(g kS). Ее типичный вид для поверхностного плазмон-поляритона на границе
металл-воздух показан на рис. 28. Центр линии kS0 kSпрактически совпадает с волновым числом "идеального" возбуждения, определяемым соотношением ks k0*sqrt(εεεε, а значение μв максимуме линии M и ее ширина Δопределяются диссипативными потерями в скин-слое металла. При этом
M=2*
=L/sqrt(2);
Для определенности отметим, что первая из формул (5.16) справедлива только для ближней ИК-области спектра. Если принять, например, что ПЭВ возбуждается на длине волны 1 мкм при нормальном падении света на резо- нансную решетку, то, как это следует из (5.16),
Δ≈50–200 см-1, M
107 см-1
Отсюда следует, что поляритонная линия достаточно узкая, а продольное электрическое поле ПЭВ x E сравнивается с полным полем на поверхности t Eпри высоте резонансной решетки всего лишь h
10−3λ
МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН
САМАРКАНДСКИЙ ФИЛИАЛ ТАШКЕНТСКОГО УНИВЕРСИТЕТА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ИМЕНИ МУХАММАДА АЛ-ХОРАЗМИЙ
ФАКУЛЬТЕТ:
«ТЕЛЕКОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ И ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ»
Самостоятельная работа №1
по предмету: Электромагнитные поля и волны
ТЕМА: Поверхностный эффект. Волны на поверхности раздела двух диэлектрических сред.
Выполнил(а): Файзуллаев Ф. С
Проверил(а): Егамов Ш. В
САМАРКАНД – 2023
Поверхностные волны – это волны, которые распространяются вдоль границы раздела двух сред и приникают в эти среды на расстояние, меньшее длины волны. В поверхностных волнах вся энергия сосредоточена в узкой окрестности границы раздела, и состояние поверхности существенно влияет на их распространения. Именно поэтому поверхностные волны являются источником информации о состоянии поверхности. Более того, взаимодействие объемных и поверхностных волн может приводить к различным поверхностным эффектам, таким как генерация гармоник, вращение плоскости поляризации при отражении и так далее.
Волны такого типа возникают при падении объемной волны из диэлектрика на поверхность металла что обуславливается некоторыми особеностями распространения волн в средах со своободными зарядами,примерами которых являются металлы. При падении волны на такое вещество,свободные электроны колеблются под действием внешнего переменного поля волны. Ионы также испытывают действие поля,но поскольку их масса относительно велика,то в первом приблиении их считают неподвижными.
Уравнение движения для электронов имеет вид:
mr'' + mr' = еЕ
Здесь Е — среднее макроскопическое поле; в отличие от диэлектриков при изучении плазмы можно считать, что действующее поле примерно равно макроскопическому; v — эффективная частота соударений электронов с ионами и нейтральными
молекулами.
Учитывая,что поле Е волны переменно: Е ехр (—i t) ;
r'=eE/m(-i ); Поляризация будет равна:
j = eNr = DР/dt = —iР, P = i*(e^2NE/m(-i));
ε=1 — p^2/(^2+^2)+ i*p^2()/(^2-^2);
Мнимая часть диэлектрической проницаемости есть проводимость среды, то есть внешнее,даже переменное поле проникает в металл на расстояния порядка длины волны,за счет того что электрон,двигаясь в нем,создают аналогичное поле(экранируют внешнее). При p электоны не «успевают» за полем,и металл становится прозрачным.
Также стоит отметить,что плазмонные волны являются ТМ-волнами,в которых вектор поляризации перпендикулярен плоскости падения.
Действительно,если бы в рассматриваемой волне имелась компонента,параллельная плоскости падения,то она вынуждала бы электроны в тонком пограничном слое колебаться туда-обратно через поверхность металла. Но электроны не могут уйти с поверхности раздела из-за потенциального барьера,то есть энергия данной компоненты поляризации гаснет на поверхностном энергетическом барьере.
Для возбуждения поверхностных волн необходимо условие фазоаго синхронизма возбуждаемой волны с возбуждающей. Другими словами, если в кристаллической структуре имеет место
согласование фаз, то величина выходного сигнала будет значи- значительной; если же согласование фаз отсутствует, то можно полу- получить лишь весьма слабый сигнал.
Возникает вопрос, что происходит с энергией в случае отсут- отсутствия согласования фаз в структуре? Или, точнее, что происхо- происходит с частью энергии, которая расходуется на генерацию тех
частотных компонент нелинейной поляризации, для которых отсутствует согласование фаз? Этот вопрос важен, поскольку такие частотные компоненты всегда существуют. Если
бы эта энергия терялась (например, вследствие поглощения), то любой нелинейный оптический процесс всегда сопровождался бы сильным затуханием.
Ответ на этот вопрос заключен в фазе сигнала. Пренебрегая тензорной природой ε, напишем формулу плотности потока энергии:
DP/dt= (1/4)[ε*Dε/dt+H*DH/dt]+ε*Dp/dt
Член в скобках в правой части уравнения есть скорость возрастания энергии электромагнитной волны в вакууме; по- последний член — энергия, затраченная на изменение электриче- электрической поляризации. Энергия поляризации равна
W=*Dp/dt;
усредненная по периоду, большому по
сравнению с 2. Таким образом, средняя поглощенная энергия равна
W=1/2Psin разность фаз между волной поляризации и электро- магнитной волной. При генерируемый сигнал отстает от падающей волны на 90 градусов-это означает,что энергия W отрицательна,т.е энергия переходит от волны поляризации к электромагнитной волне,но при ≠ это вообще не верно.При дальнейшем распространении волны поток энерги меняет знак-вместо перехода энергии от электромагнитной волны к волне поляризации происходит обратный процесс.Иначе говоря,энергия генерируемой волны возвращается исходному излучению.
Методы возбуждения ПЭВ
Хотя ПЭВ является собственной модой плоской границы раздела, для ее возбуждения светом нужны специальные условия, поскольку волновой вектор ПЭВ Sk больше волнового вектора света k0 на той же частоте. К настоящему времени разработаны два эффективных метода возбуждения ПЭВ светом (рис. 2): призменный и решеточный.
Призменный метод возбуждения ПЭВ
Преобразование света в ПЭВ призменным методом основано на явлении нарушенного полного внутреннего отражения при падении p-поляризованного излучения (поляризованного в плоскости падения) на ПАС со стороны оптиче- ски более плотной среды. Угол падения θ выбирается из известного в оптике условия
θ arcsin(sqrt(ε1 ε3 , ε1 ε3
где ε3 – диэлектрическая проницаемость материала призмы. Метод существует в двух модификациях: геометрия Отто (рис. 1 а) и геометрия Кречманна (рис.1б). Этим методом ПЭВ возбуждается на гладкой поверхности, поскольку притрансформации объемного излучения в ПЭВ удается согласовать их волновые векторы. В большинстве случаев источниками света в соответствующих устройствах генерации ПЭВ являются лазеры.
Эффективность преобразования падающего объемного излучения в ПЭВ в схеме Отто, чаще применимой для ИК-области спектра (СО2-лазеры), достигает десятых долей, а в геометрии Кречманна для видимого света практически доходит до 1. Однако в последнем слу-чае вывод ПЭВ за пределы призмы
затруднен, и ПАС обычно наносится на еегрань в виде тонкой пленки. Обратное преобразование ПЭВ в объемное излучение также возможно с помощью призм.
Двупризменный метод возбуждения и детектирования ПЭВ в геометрии
Отто успешно используется в ИК-спектроскопии твердого тела. Длина пробега ПЭВ вдоль поверхности может достигать нескольких сантиметров, она весьма чувствительна к процессам в поглощающем слое, состоянию поверхности и его изменениям, наличию адсорбированных слоев, пленок, шероховатости и др.
Это обеспечивает возможность исследовать поверхности и границы раздела с помощью ПЭВ, а также осуществлять прецизионные оптические измерения, на- пример измерять малое поглощение высоко отражающих металлических зеркал на уровне 0,01 с ошибкой не более до 10%..
Рис.1 Возбуждение ПЭВ светом: а - призменный метод, геометрия Отто; б - призменный метод, геометрия Кречманна; в - решеточный метод. 1 - диэлектрик
( воздух); 2 - поверхностно-активная среда; 3 - призма; 4 - падающее излучение; 5 - ПЭВ; 6 - зеркально отраженное излучение; 7 - решетка; l - зазор размером
λ; d- период решетки.МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН
САМАРКАНДСКИЙ ФИЛИАЛ ТАШКЕНТСКОГО УНИВЕРСИТЕТА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ИМЕНИ МУХАММАДА АЛ-ХОРАЗМИЙ
ФАКУЛЬТЕТ:
«ТЕЛЕКОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ И ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ»
Самостоятельная работа №1
по предмету: Электромагнитные поля и волны
ТЕМА: Поверхностный эффект. Волны на поверхности раздела двух диэлектрических сред.
Выполнил(а): Файзуллаев Ф. С
Проверил(а): Егамов Ш. В
САМАРКАНД – 2023
Поверхностные волны – это волны, которые распространяются вдоль границы раздела двух сред и приникают в эти среды на расстояние, меньшее длины волны. В поверхностных волнах вся энергия сосредоточена в узкой окрестности границы раздела, и состояние поверхности существенно влияет на их распространения. Именно поэтому поверхностные волны являются источником информации о состоянии поверхности. Более того, взаимодействие объемных и поверхностных волн может приводить к различным поверхностным эффектам, таким как генерация гармоник, вращение плоскости поляризации при отражении и так далее.
Волны такого типа возникают при падении объемной волны из диэлектрика на поверхность металла что обуславливается некоторыми особеностями распространения волн в средах со своободными зарядами,примерами которых являются металлы. При падении волны на такое вещество,свободные электроны колеблются под действием внешнего переменного поля волны. Ионы также испытывают действие поля,но поскольку их масса относительно велика,то в первом приблиении их считают неподвижными.
Уравнение движения для электронов имеет вид:
mr'' + mr' = еЕ
Здесь Е — среднее макроскопическое поле; в отличие от диэлектриков при изучении плазмы можно считать, что действующее поле примерно равно макроскопическому; v — эффективная частота соударений электронов с ионами и нейтральными
молекулами.
Учитывая,что поле Е волны переменно: Е ехр (—i t) ;
r'=eE/m(-i ); Поляризация будет равна:
j = eNr = DР/dt = —iР, P = i*(e^2NE/m(-i));
ε=1 — p^2/(^2+^2)+ i*p^2()/(^2-^2);
Возбуждение ПЭВ на решетке
Свойством возбуждать ПЭВ обладают и дифракционные решетки, нане- сенные на поверхностно-активную среду (рис. 1 в) и рассеивающие излучение
под определенными углами. Когда при некоторых углах падения света θди- фрагированная волна оказывается направленной вдоль поверхности, она пред- ставляет собой ПЭВ. Волновой вектор g⃗ решетки с периодом dнаправленный перпендикулярно ее штрихам и по модулю равеный 2π d(резонансная, гармо- ническая решетка) связан с волновым вектором ПЭВ kS
и векторной проекцией ktволнового вектора излучения k0
на поверхность (рис. 2 а) равенством
kt+ mg=KS
m1,2,...; kt k0*sinθ
Оно выражает закон сохранения импульса (иначе – условие фазового синхро- низма) при преобразовании света в поверхностные поляритоны без изменения частоты. В выражении m–порядок дифракции, который будем считать равным единице. Взаимную ориентацию векторов kS,k tи g⃗ удобно поясняет круговая векторная диаграмма (рис. 2б).Рис. 2. Взаимная ориентация (а) и круговая диаграмма (б) векторов,
определяющих преобразование света в ПЭВ на гармонической решетке ξ ( y) h cos(gy) с амплитудой h , пространственной частотой g и периодом d 2πg.k t- проекция волнового вектора k0 на плоскость поверхности; ks-волновой вектор ПЭВ; krволновой вектор отраженного излучения; g⃗-волновой вектор решетки;n⃗- нормаль к усредненной поверхности; θ- угол падения света.
Штриховкой очерчена часть окружности радиуса Skна круговой диаграмме.
Из количественной теории преобразования света в ПЭВ на периодиче- ских решетках следует, что для излучений p-и s-поляризаций продольный
компонент поля ПЭВ на поверхности Exи действующее внешнее поле Etпро- порциональны, а соответствующий коэффициент пропорциональности в пер- вом приближении линейно зависит от высоты h резонансной гармонической решетки. Для случая нормального падения излучения эта связь наиболее про- ста:
Ex μEh
Параметр μ, называется коэффициентом преобразования и является ком- плексной величиной, зависящей от волнового числа поверхностного полярито- на kS . Модуль этого параметра μ , рассматриваемый как функция kS,фактиче-
ски описывает форму линии возбуждения поверхностного поляритона коге- рентным излучением при нормальном падении на резонансную решетку
(g kS). Ее типичный вид для поверхностного плазмон-поляритона на границе
металл-воздух показан на рис. 28. Центр линии kS0 kSпрактически совпадает с волновым числом "идеального" возбуждения, определяемым соотношением ks k0*sqrt(εεεε, а значение μв максимуме линии M и ее ширина Δопределяются диссипативными потерями в скин-слое металла. При этом
M=2*
=L/sqrt(2);
Для определенности отметим, что первая из формул (5.16) справедлива только для ближней ИК-области спектра. Если принять, например, что ПЭВ возбуждается на длине волны 1 мкм при нормальном падении света на резо- нансную решетку, то, как это следует из (5.16),
Δ≈50–200 см-1, M
Виноградова,Руденко,Сухоруков. Теория волн, М.:Просвящение,1990 г.
Ф. Цернике, Дж. Мидвинтер,Прикладная нелинейная оптика М.: Мир, 1976 г.
N. V. Kuzmin, Interference Effects with Surface Plasmons. Leiden University, 2008 г.
М.Н. Либенсон, Е.Б. Яковлев, Г.Д. Шандыбина.Взаимодействие излучения с веществом (силовая оптика). Конспект лекций под редакцией Вейко В.П. СПб.: СПбГУ ИТМО, 2008
Волкова З.А. Поверхностные электромагнитные волны. М.:2005 г.