Файл: Цель работы Разработка в среде программирования Visual prolog экспертной системы, которая, на основе алгоритма нечёткого вывода Мамдани, решает задачу из Лабораторной работы 2. Теоретические сведения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цель работы: Разработка в среде программирования Visual PROLOG экспертной системы, которая, на основе алгоритма нечёткого вывода Мамдани, решает задачу из Лабораторной работы №2.
1. Теоретические сведения
Алгоритм Мамдани предложен одним из первых для управления паровым двигателем и описывается следующим образом.
Формирование базы правил систем нечеткого вывода и введение нечеткости для входных переменных. Предположим, что база состоит из двух правил (см. рис. 1) с двумя входами и одним выходом:
Правило 1: ЕСЛИ x1 есть А11 И x2 есть А12 ТО y есть B1,
Правило 2: ЕСЛИ x1 есть А21 И x2 есть А22 ТО y есть B2.
Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Правила, степень истинности условий которых отлична от нуля, считаются активными.
Активизация подзаключений в нечетких правилах продукций выполняется с помощью min-активизации по формуле:
μ'(y) = min{ci, μ'(y)};
причем, для сокращения времени вывода учитываются только активные правила.
Аккумулирование заключений нечетких правил продукций выполняется с помощью max-объединения по формуле:
μ D(x) = max{ μ A (x), μ B (x)} (
для объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным.
Дефаззификация выходных переменных выполняется с использованием метода центра тяжести:
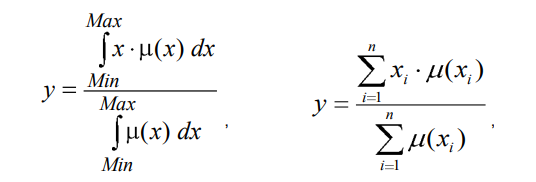
или метод центра площади:
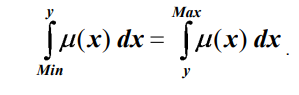
Схема экспертной системы
Пр.1: Если m = M1 AND fc = FC1, то p = P1.
Пр.2: Если m = M2 AND fc = FC2, то p = P2.
Пр.3: Если m = M3 AND fc = FC3, то p = P3.
Пр.4: Если m = M4 AND fc = FC4, то p = P4.
DOMAINS
ALFA1=REAL
ALFA2=REAL
ALFA3=REAL
ALFA4=REAL
PREDICATES
MAIN(REAL,REAL)
RULE1(REAL,REAL,REAL)
RULE2(REAL,REAL,REAL)
RULE3(REAL,REAL,REAL)
RULE4(REAL,REAL,REAL)
F1(REAL,REAL)
F2(REAL,REAL)
F3(REAL,REAL)
F4(REAL,REAL)
F5(REAL,REAL)
F6(REAL,REAL)
F7(REAL,REAL)
F8(REAL,REAL)
FB1(REAL,REAL)
FB2(REAL,REAL)
FB3(REAL,REAL)
FB4(REAL,REAL)
MIN(REAL,REAL,REAL)
MAX(REAL,REAL,REAL)
SREZ(REAL,REAL,REAL,REAL,REAL,REAL,REAL,REAL,REAL,REAL)
CLAUSES
MAIN(T,N):-RULE1(T,N,A1),RULE2(T,N,A2),RULE3(T,N,A3),RULE4(T,N,A4), ALFA1=A1,ALFA2=A2,ALFA3=A3,ALFA4=A4,SR=0,INTG=0,I=1,DY=20/25,SREZ(I,SR,DY,ALFA1,ALFA2,ALFA3,ALFA4,SROK,INTG,INTG2),REZ=INT
G2/SROK, WRITE("\n\n\n\n >>>> DENUMERATOR = ",SROK,"NUMERATOR =", INTG2,"REZ = ",REZ, " let").
RULE1(T,N,A1):-F1(T,T1),F2(N,N1),MIN(T1,N1,A1).
RULE2(T,N,A2):-F3(T,T2),F4(N,N2),MIN(T2,N2,A2).
RULE3(T,N,A3):-F5(T,T3),F6(N,N3),MIN(T3,N3,A3).
RULE4(T,N,A4):-F7(T,T4),F8(N,N4),MIN(T4,N4,A4).
F1(T,T1):-T<70,T1=0;
T>=70,T<90,T1=(T-70)/20;
T>=90,T1=1.
F2(N,N1):-N<1.5,N1=1;
N>=1.5,N<03,N1=(N-1.5)/1.5;
N>=3,N1=1.
F3(T,T2):-T<40,T2=0;
T>=40,T<60,T2=(T-40)/20;
T>=60,T<80,T2=(80-T)/20;
T2=0.
F4(N,N2):-N<1.5,N2=1;
N>=1.5,N<3,N2=(3-N)/1.5;
N2=0.
F5(T,T3):-T<40,T3=0;
T>=40,T<60,T3=(T-40)/20;
T>=60,T<80,T3=(80-T)/20;
T>=80,T3=0.
F6(N,N3):-N<1.5,N3=0;
N>=1.5,N<3,N3=(N-1.5)/1.5;
N>=3,N3=1.
F7(T,T4):-T<70,T4=0;
T>=70,T<90,T4=(T-70)/20;
T>=90,T4=1.
F8(N,N4):-N<1.5,N4=1;
N>=1.5,N<3,N4=(3-N)/1.5;
N>=3,N4=0.
% FUNCTION OF BILONGING "LIFE DURATION LOW"
FB1(Y,SR1):-Y<2,SR1=0;
Y>=2,Y<4,SR1=(Y-2)/2;
Y>=4,Y<6,SR1=(6-Y)/2;
SR1=0.
% FUNCTION OF BILONGING "LIFE DURATION LONG"
FB2(Y,SR2):-Y<5,SR2=0;
Y>=5,Y<10,SR2=(Y-5)/5;
Y>=10,Y<=20,SR2=1.
% FUNCTION OF BILONGING "LIFE DURATION MID-1"
FB3(Y,SR3):-Y<5,SR3=0;
Y>=5,Y<7,SR3=(Y-5)/2;
Y>=7,Y<9,SR3=(9-Y)/2;
SR3=0.
% FUNCTION OF BELONGING "LIFE DURATION MID-2"
FB4(Y,SR4):-Y<2,SR4=0;
Y>=2,Y<5,SR4=(Y-2)/3;
Y>=5,Y<8,SR4=(8-Y)/3;
SR4=0.
MIN(ARG1,ARG2,ARGM):-ARG1>=ARG2,ARGM=ARG2;
ARGM=ARG1.
MAX(ARG1,ARG2,ARGMAX):-ARG1>=ARG2,ARGMAX=ARG1;
ARGMAX=ARG2.
SREZ(I,SR,DY,ALFA1,ALFA2,ALFA3,ALFA4,SR2,INTG,INTG2):-I<=12,Y=I*DY,FB1(Y,FY1),FB2(Y,FY2),FB3(Y,FY3),FB4(Y,FY4), MIN(ALFA1,FY1,FMIN1),MIN(ALFA2,FY2,FMIN2),MIN(ALFA3,FY3,FMIN3),MIN(ALFA4,FY4,FMIN4),MAX(FMIN1,FMIN2,FMAX1),MAX(FMIN3,FMIN4,FMAX2),MAX(FMAX1,FMAX2,FMAX),
% denominator at formula for center of square
SR1=SR+FMAX*DY,
% numerator at formula for center of square
INTG1=INTG+Y*FMAX*DY,
IP=I+1,
SREZ(IP,SR1,DY,ALFA1,ALFA2,ALFA3,ALFA4,SR3,INTG1,INTG3),
SR2=SR3,INTG2=INTG3;
I>12,
SR2=SR,INTG2=INTG.
GOAL
WRITE("\n\n Input the water temperature (40-100) -->>"),
READREAL(T),
WRITE("\n\n Input the concentration of aggressive substance in water (anything)-->> "),
READREAL(N),
MAIN(T,N),
READREAL(C).
Выводы: в ходе этой работы мы научились разрабатывать экспертные системы с нечеткими продукционными правилами и их реализовывать.