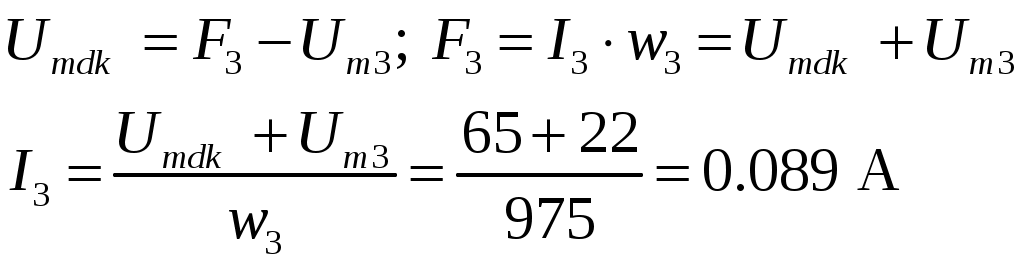Задача 1.Для линии без потерь, параметры которой заданы, определить:1. Комплексные напряжения и ток в начале линии, а также коэффициент полезного действия.2. 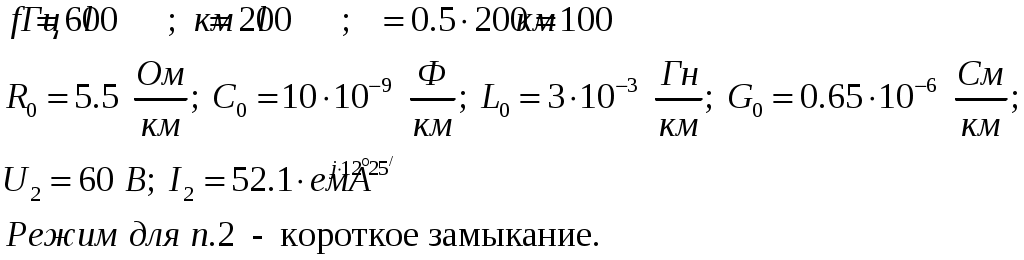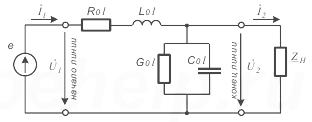Приняв заданную линию за линию без потерь (R₀=0 и G₀=0), построить график распределения действующего значения напряжения вдоль линии при заданной нагрузке и при холостом ходе линии или коротком замыкании на выходных зажимах, если напряжение на входе линии равно определенному в п.1.Рисунок 1. Схема длинной линии.Заданный расчет производим в программе MathCad. 1. 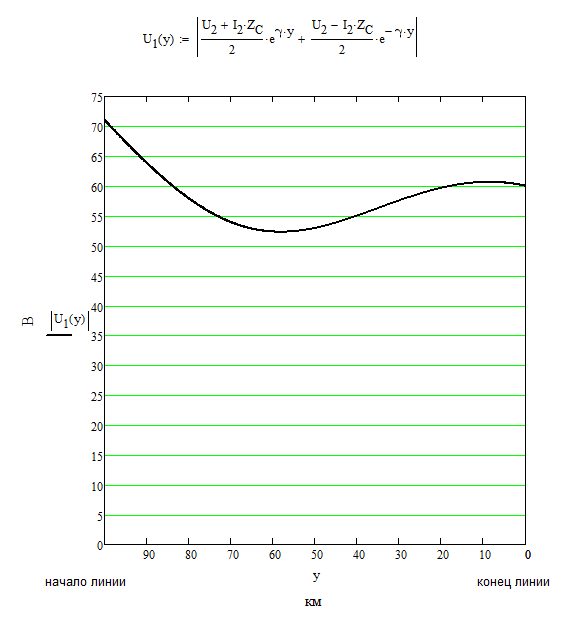Расчет заданной линии:В результате расчета получены значения напряжения и тока в начале линии: КПД линии Строим график распределения действующего значения напряжения.Рисунок 2. График распределения действующего значения напряжения вдоль линии.2. 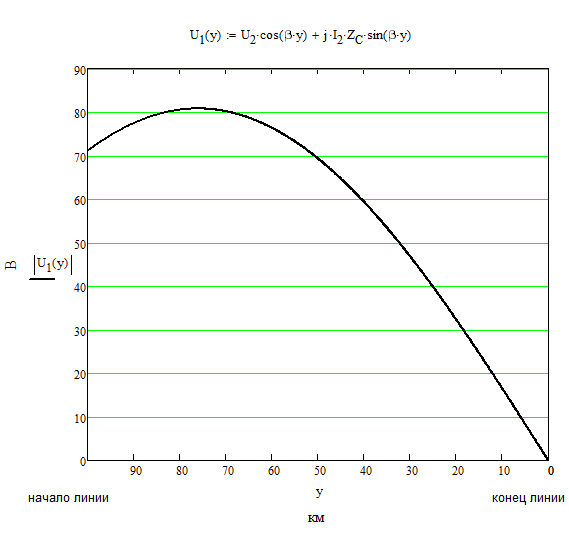Расчет для линии без потерь при коротком замыкании.В результате расчета получены значения напряжения и тока в начале линии: Ток в конце линии: Строим график распределения действующего значения напряжения.Рисунок 3. График распределения действующего значения напряжения вдоль линии без потерь.Задача 2.Методом последовательных приближений (методом итераций) рассчитать заданную электрическую цепь. В электрической цепи один из резисторов обладает нелинейным сопротивлением.

---

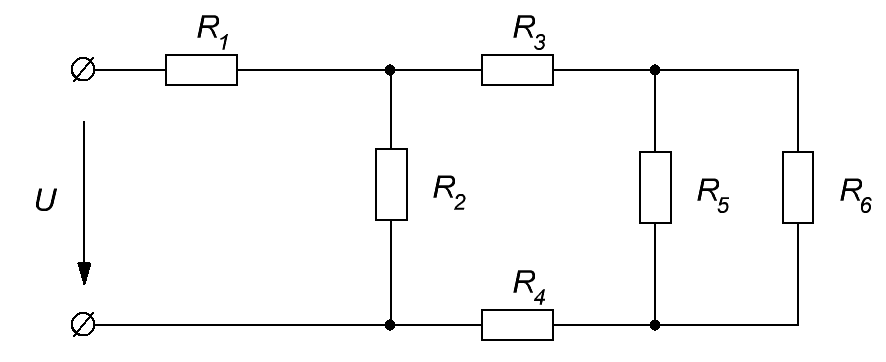
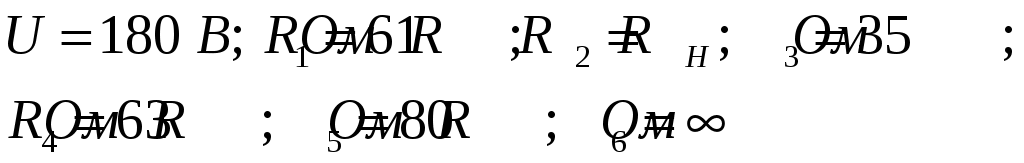
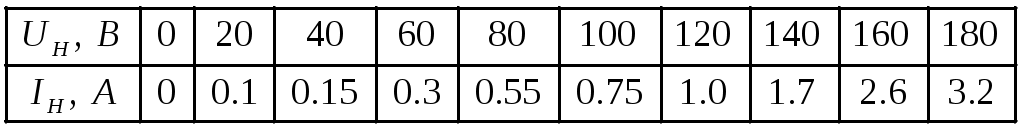
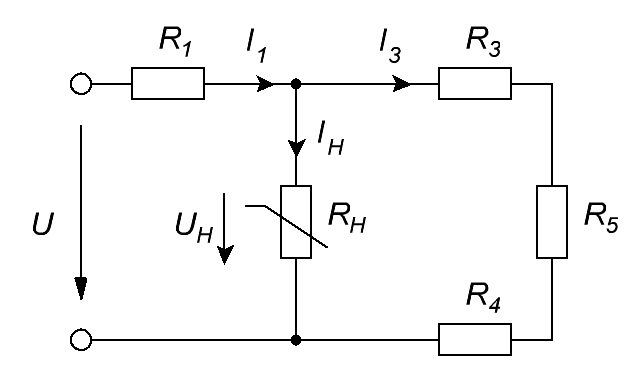
Определить:1. Ток и напряжение на нелинейном элементе R_H при заданных параметрах цепи.2. Токи в ветвях.Рисунок 1. Общий вид заданной схемы.Заданные параметры цепи:Вольт-амперная характеристика нелинейного элемента.1. Составляем схему электрической цепи в соответствии с заданием по варианту. На схеме обозначаем токи в ветвях и задаем их направления.Рисунок 2. Расчетная схема цепи.2. Для расчета параметров нелинейного сопротивления преобразовываем заданную схему к эквивалентному генератору относительно нелинейного сопротивления. 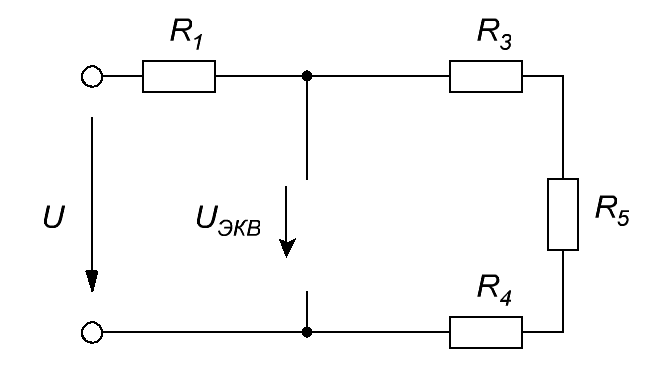Рисунок 3. 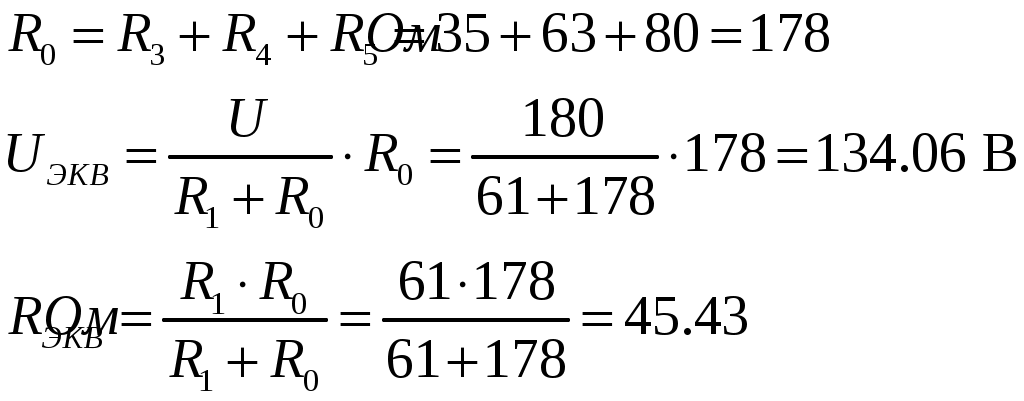Схема для расчета параметров эквивалентного генератора.Рассчитываем параметры эквивалентного генератора.3. 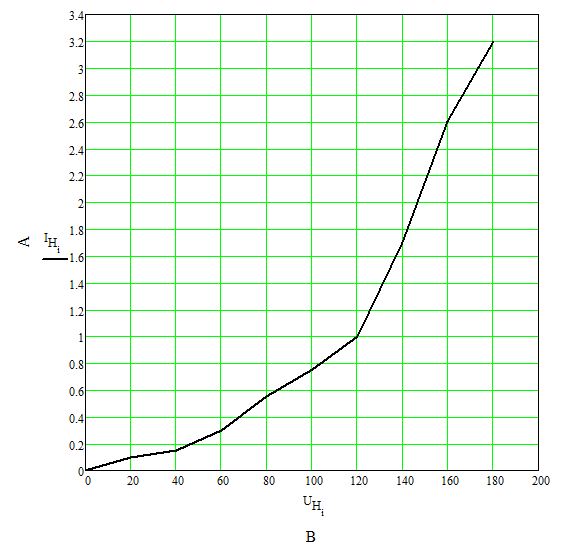По заданным параметрам строим вольт-амперную характеристику нелинейного элемента.Рисунок 4. Вольт-амперная характеристика нелинейного сопротивления.4. 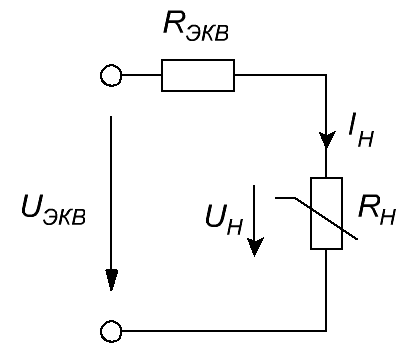Для схемы эквивалентного генератора получим выражение, определяющее зависимость напряжения на нелинейном элементе от тока нелинейного элемента.Рисунок 5. 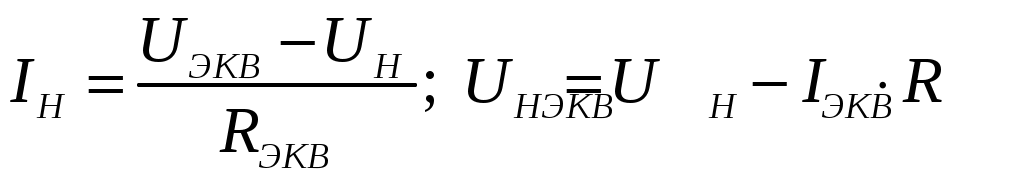Схема эквивалентного генератора нелинейного сопротивления.5. Производим расчет цепи методом итераций.Для нулевого приближения задаем ток нелинейного элемента: Напряжение нелинейного элемента: По полученному значению, используя заданную вольт-амперную характеристику находим ток нелинейного элемента в первом приближении.По характеристике значению

---

соответствуют интервалы значений:
Ток нелинейного элемента:
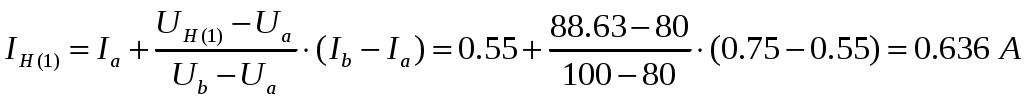
Аналогичным образом, производим последующие итерации.


1-е приближение:

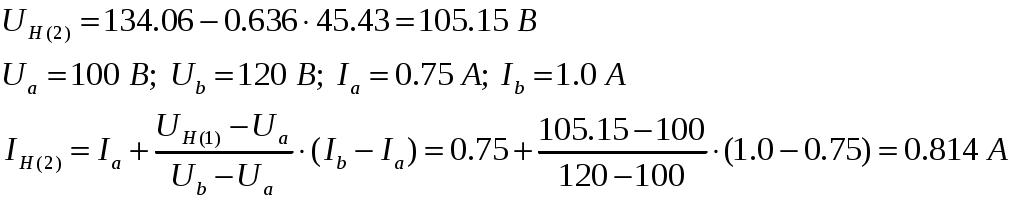
2-е приближение:

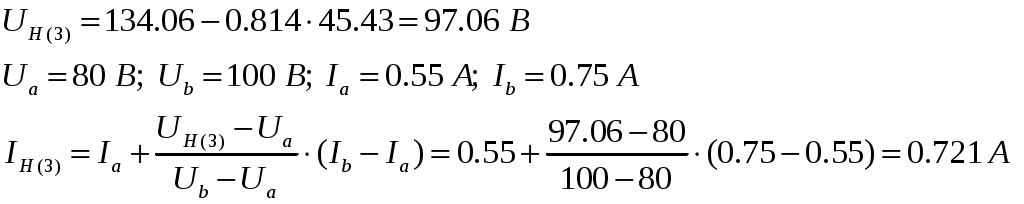
3-е приближение:

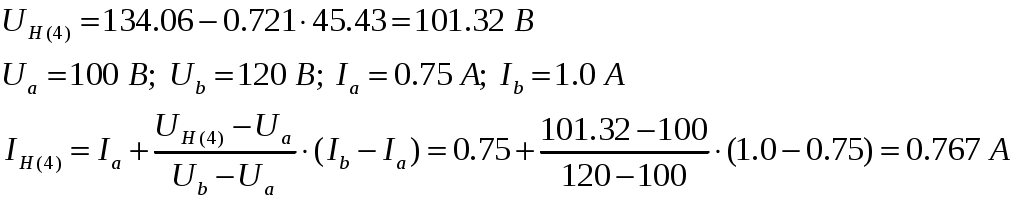
4-е приближение:

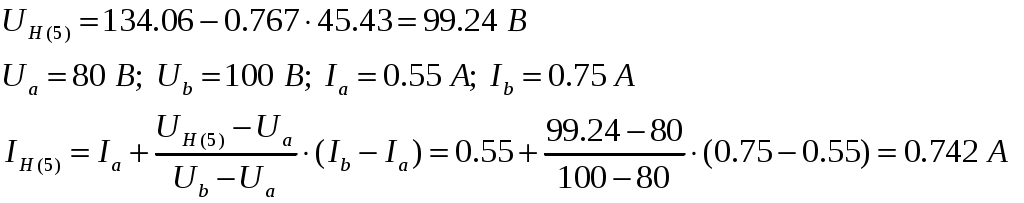
5-е приближение:


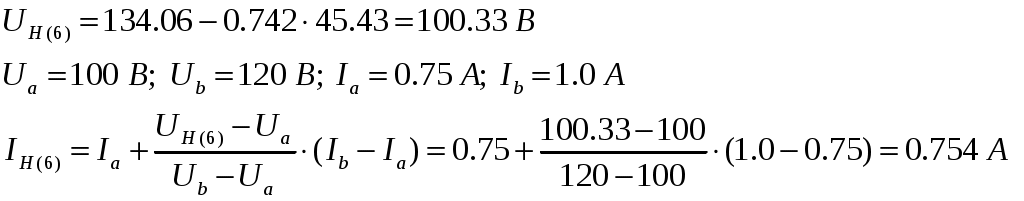
6-е приближение:

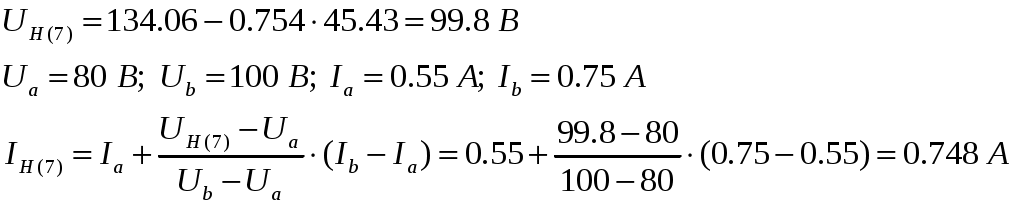
7-е приближение:

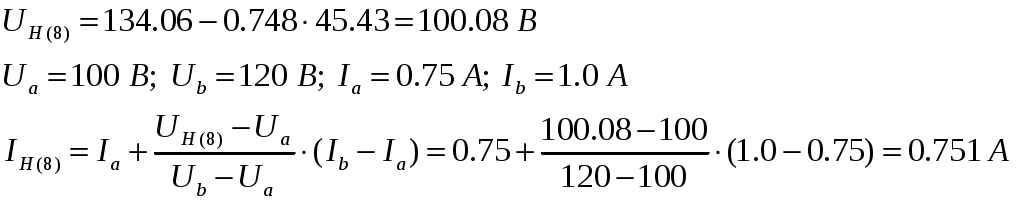
8-е приближение:

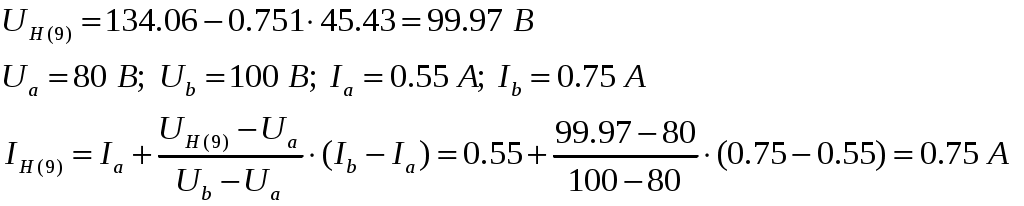
9-е приближение:


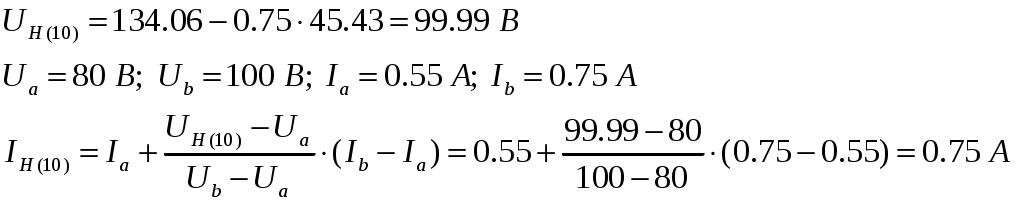
Так как при последней итерации получено:
, то эти значению и будут рабочими параметрами нелинейного элемента в заданной цепи.
Таким образом, определено:

6. По законам Кирхгофа определяем остальные токи исходной схемы:


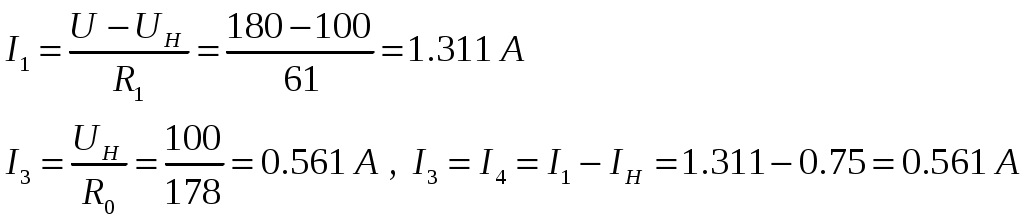
Задача 3.
Рассчитать магнитную цепь постоянного тока методом двух узлов. Определить величины, указанные в соответствии с номером варианта.
Дано:



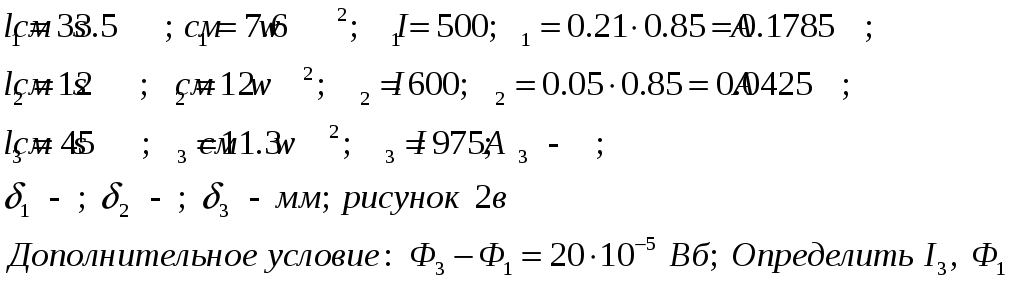
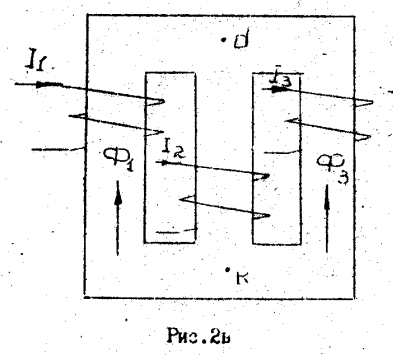
Рисунок 1. Заданная схема магнитной цепи.

Заданная кривая намагничивания:

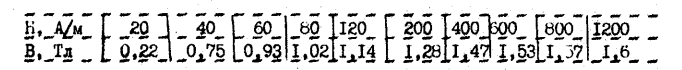
Решение:

1. Изображаем эквивалентную схему магнитной цепи. Так как в условии задано отрицательное значение тока первой катушки, то на расчетной схеме показываем МДС катушки в обратном направлении

---

, по сравнению с исходной схемой и в дальнейших расчетах ток этой катушки считаем положительным.



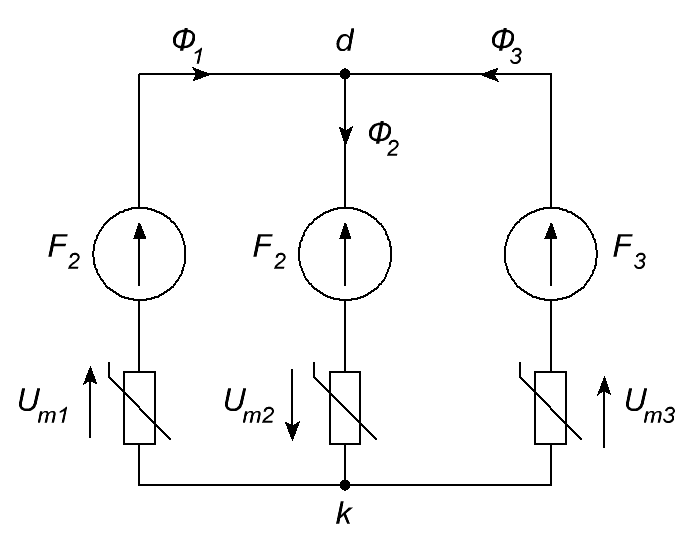
Рисунок 2. Расчетная схема магнитной цепи.

2. По полученной эквивалентной схеме составляем систему уравнений по законам Кирхгофа для магнитной цепи:



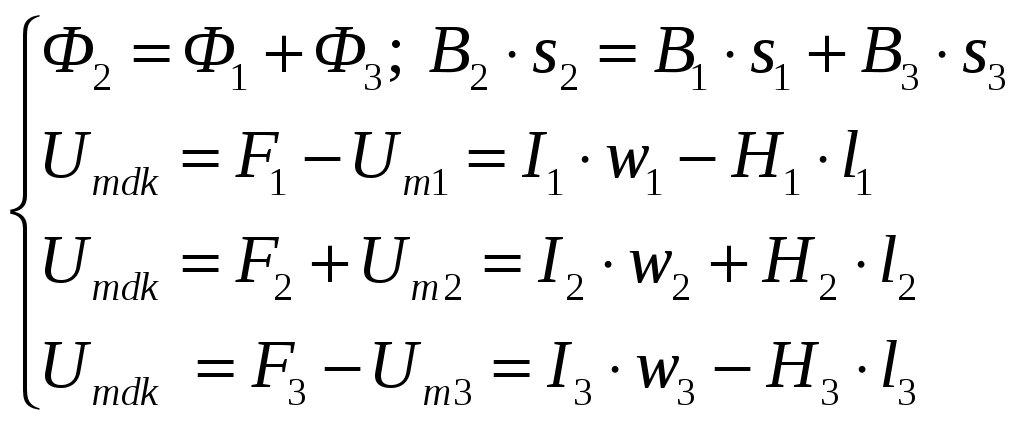
Значения магнитодвижущих сил:



3. Для определения магнитных потоков составляем расчетную таблицу и по ней строим характеристики:

1) Ф₁(U_mdk); 2) Ф₂(U_mdk) 3) Ф₃(U_m3), 4) Ф₁₁(U_mdk)

0	0	0	20	89,25	0	25,5	0	0
20	0,22	16,72	53,44	82,55	26,4	27,9	24,86	9
40	0,75	57	134	75,85	90	30,3	84,75	18
60	0,93	70,68	161,36	69,15	111,6	32,7	105,09	27
80	1,02	77,52	175,04	62,45	122,4	35,1	115,26	36
120	1,14	86,64	193,28	49,05	136,8	39,9	128,82	54
200	1,28	97,28	214,56	22,25	153,6	49,5	144,64	90
400	1,47	111,72	243,44	-44,75	176,4	73,5	166,11	180
600	1,53	116,28	252,56	-111,75	183,6	97,5	172,89	270
800	1,57	119,32	258,64	-178,75	188,4	121,5	177,41	360
1200	1,6	121,6	263,2	-312,75	192	169,5	180,8	540

---

В соответствии с условием: . Тогда, из 1-го закона Кирхгофа получаем: Точка пересечения графиков 2) Ф₂(U_mdk) и 4)Ф₁₁(U_mdk) (точка А) будет определять рабочий режим заданной магнитной цепи. По точке А определяем рабочее межузловое напряжение . 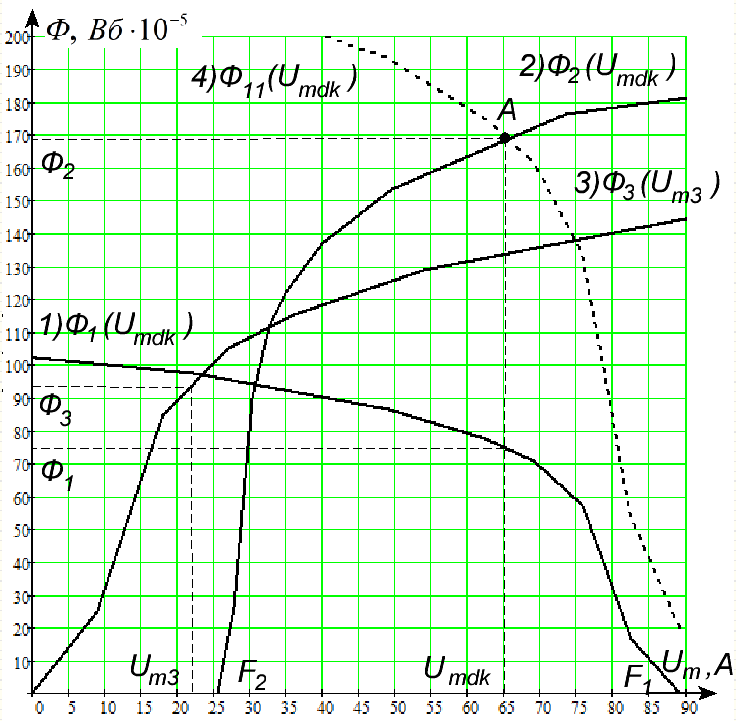При известном значении межузлового магнитного напряжения по графикам определяем значения магнитных потоков:По линии 1) Ф₁(U_mdk) Ф₁=75·10^-5 ВбПо линии 2) Ф₂(U_mdk) Ф₂=170·10^-5 ВбСоответственно, По линии 3) Ф₃(U_m3) определяем, что при значении магнитного потока Ф₃=95·10^-5 Вб значение магнитного напряжения Рисунок 3. Графический расчет магнитной цепи методом двух узлов.Из уравнения по 2-му закону Кирхгофа определяем:

---

Смотрите также файлы

• Москва 2023 Вопросы по 1 семинарскому занятию Теории психологии народов и поведения толпы (масс, элиты).docx

• Введение Проблема реализации прав ребенка существовала в России во все времена, к сожалению, она не решена и сегодня. Актуальность исследования.docx

• Цели урока мораль. Нравственность основные ценности и нормы морали. Добро и зло. Выберите.pptx

• Ремонт дороги знак дорожные работы pngпдд знак дорожные работы png знак ремонтные.pdf

• Контрольная работа 1 Задание 10 Вычислить определители а, б. Решение а. б.doc