ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА Ι

Кафедра «Высшая математика»


Контрольные работы 1,2

Выполнил:


Проверил(а):

Санкт-Петербург
2017 год

Контрольная работа 1

Задание 1.10

Вычислить определители.

а) 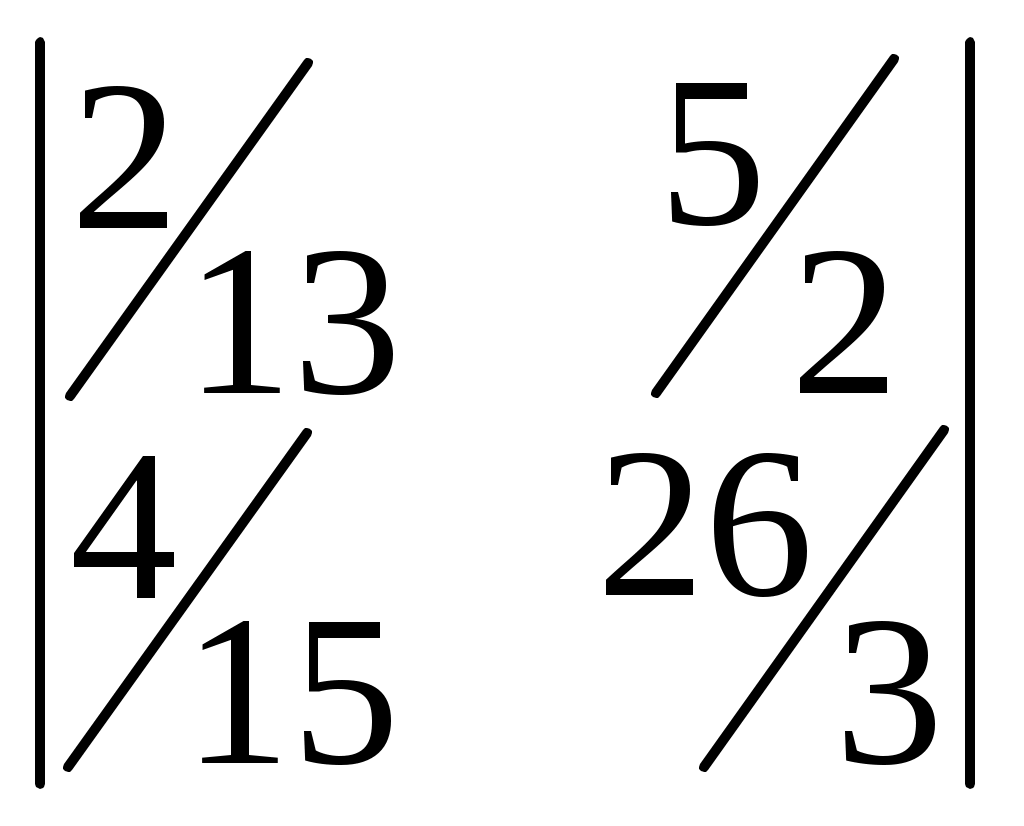, б) .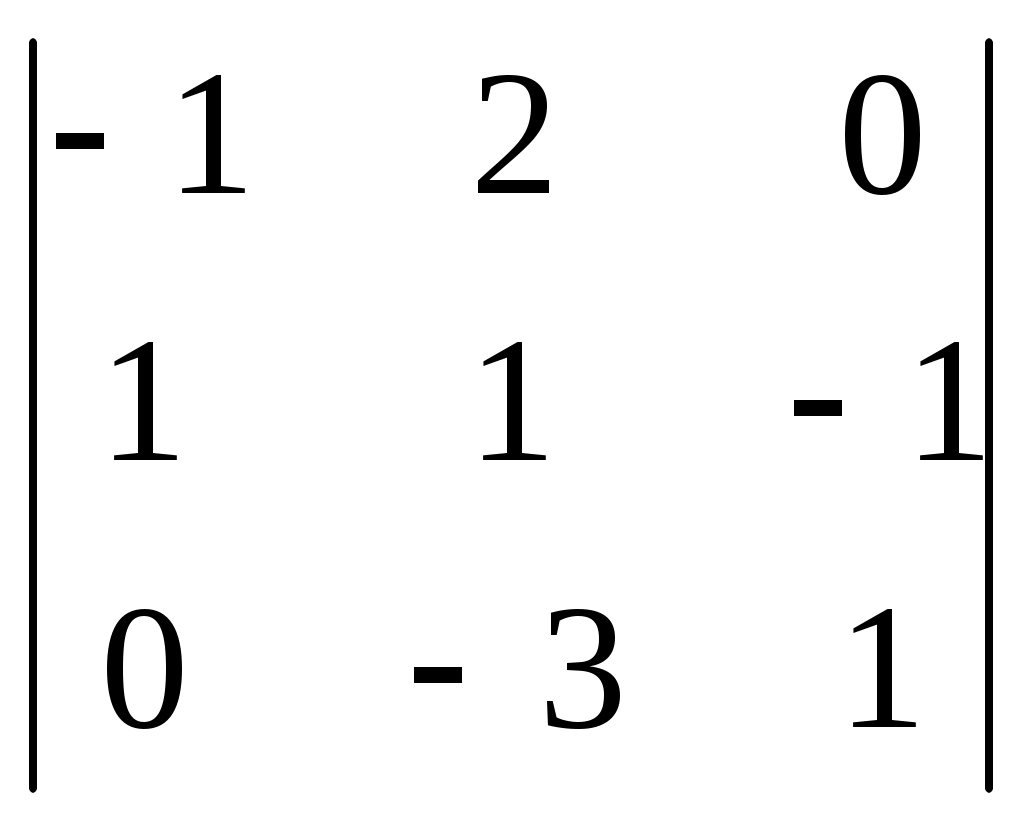

Решение

а) .


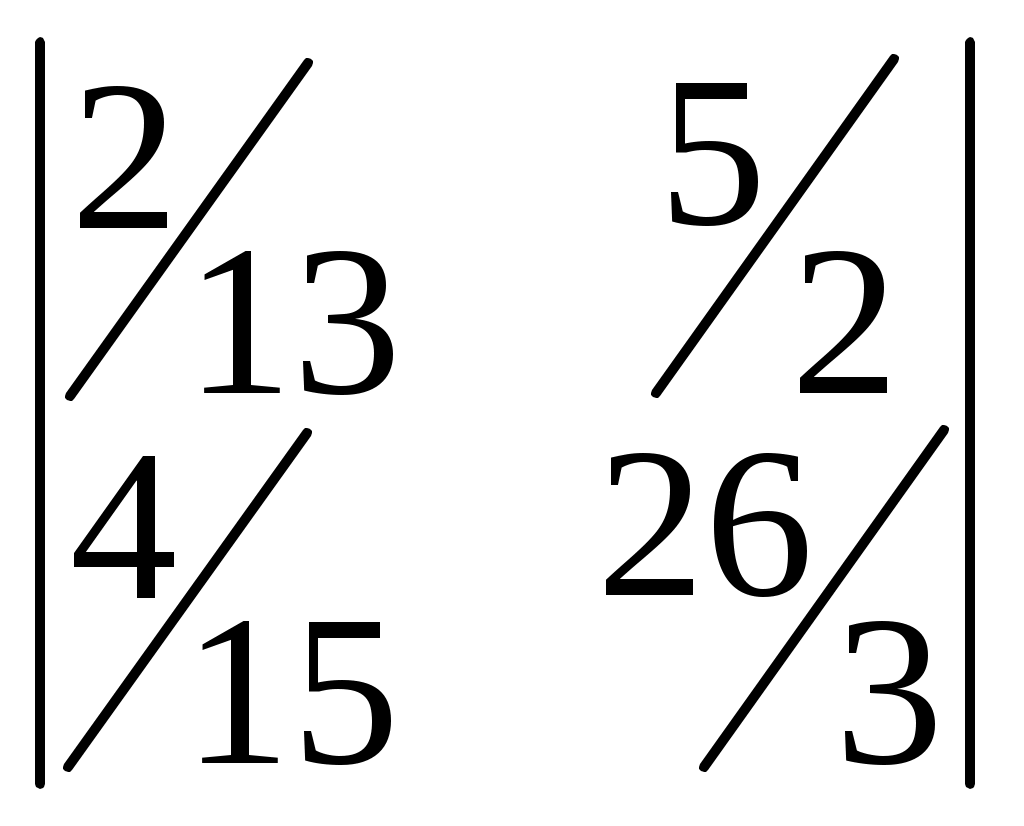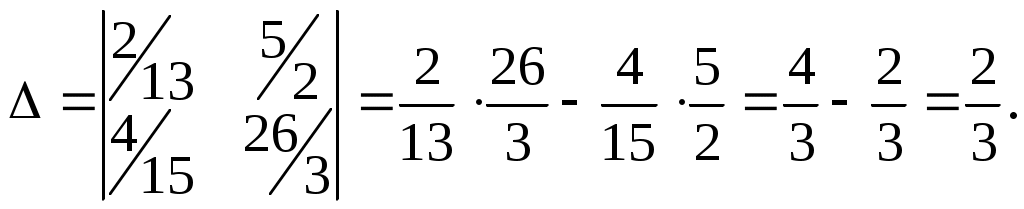
б) .

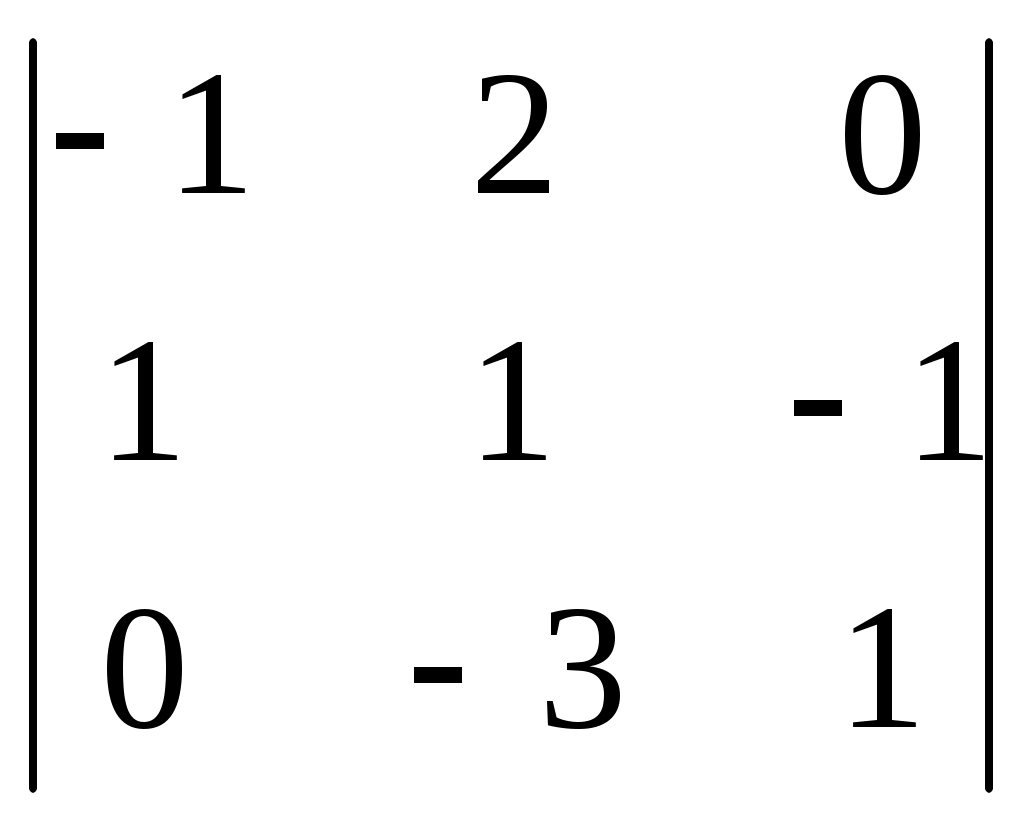Вычислим определитель разложением по элементам первой строки:

.
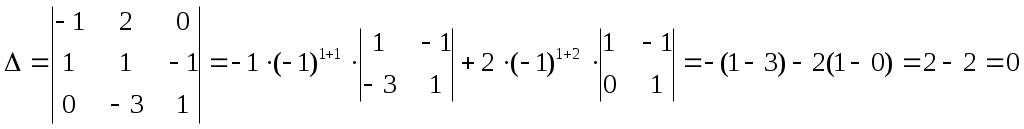Задание 1.20

Решить систему линейных уравнений методом Гаусса и по формулам Крамера. Сделать проверку.



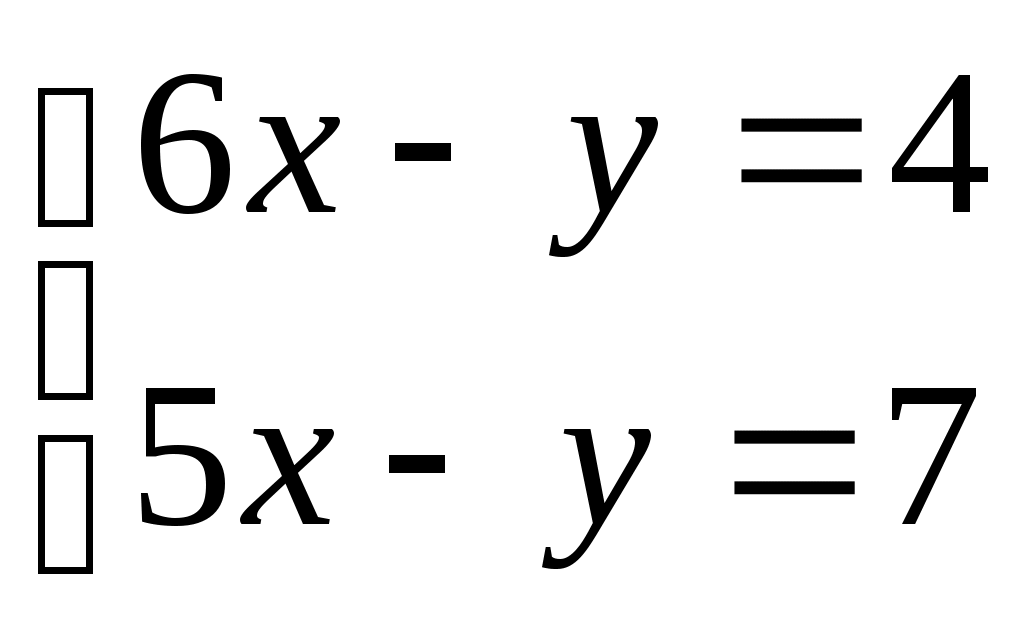
Решение

1) Метод Гаусса.

Умножим первую строку на (-1) и сложим со второй строкой:

.



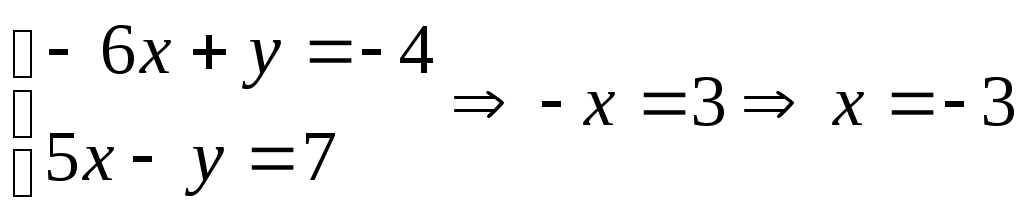Ответ:

Проверка:



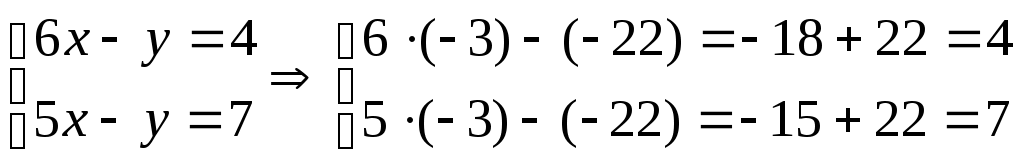
2)Формулы Крамера имеют вид: , .

Найдём определитель системы:

.

Найдём вспомогательные определители системы и :



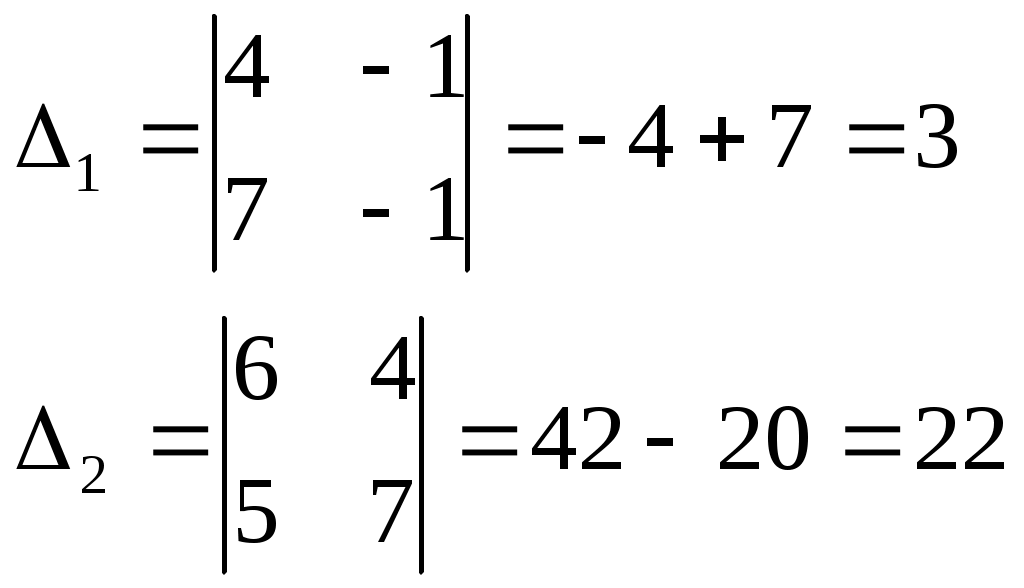
Тогда, ,

---

.
Задание 1.30

Решить систему линейных уравнений тремя методами:

а) по формулам Крамера;

б) методом Гаусса;

в) с помощью обратной матрицы.



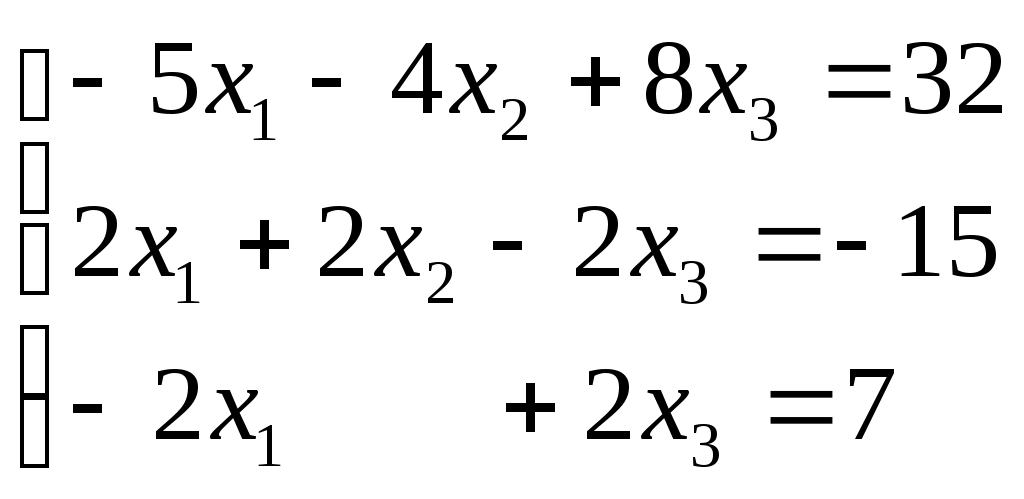
Решение

а) Формулы Крамера имеют вид: , , .

Найдём главный определитель системы :



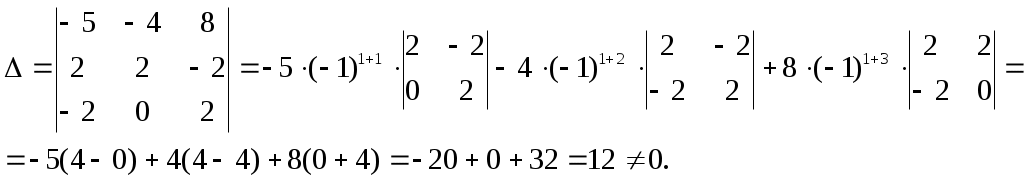
Найдём вспомогательные определители :

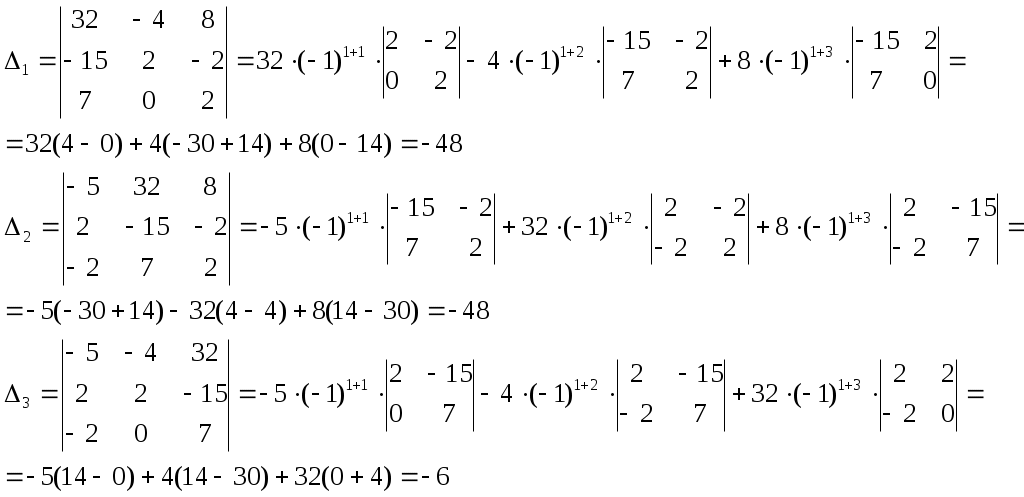Тогда,

, , .

Проверка:


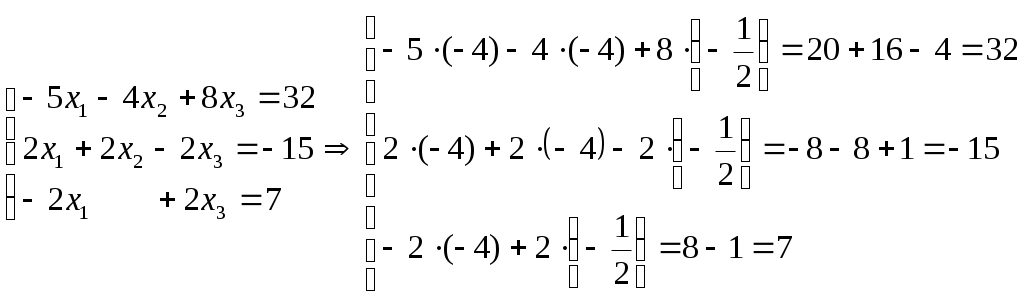
б) метод Гаусса:



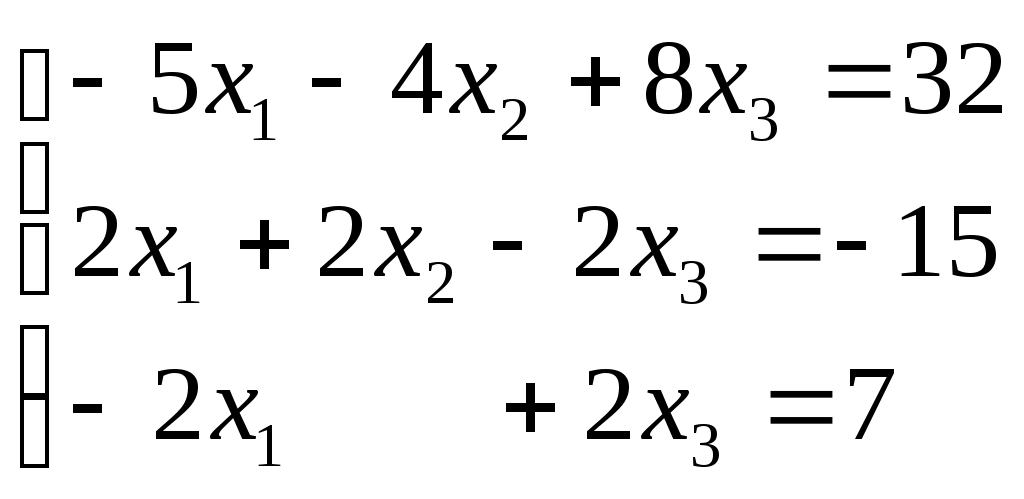
Запишем систему в виде расширенной матрицы:



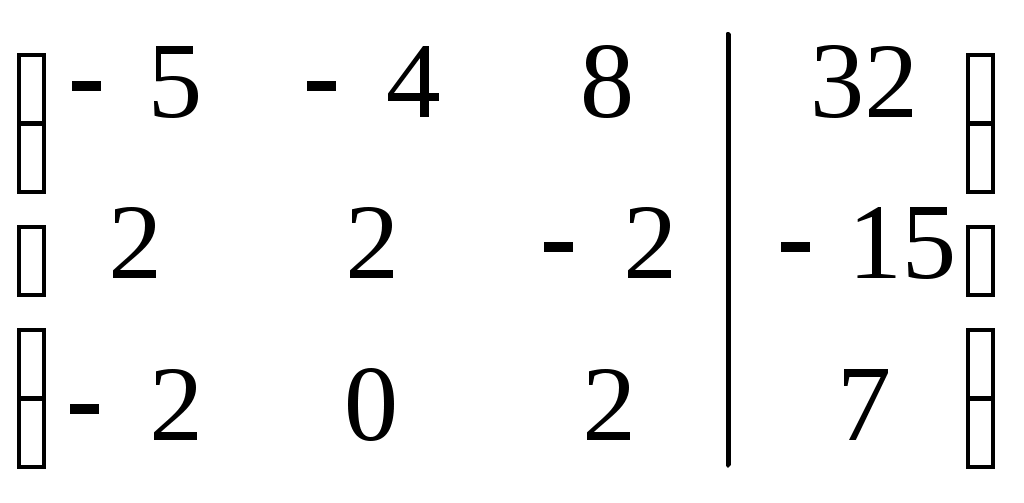
Первую строку разделим на -5:



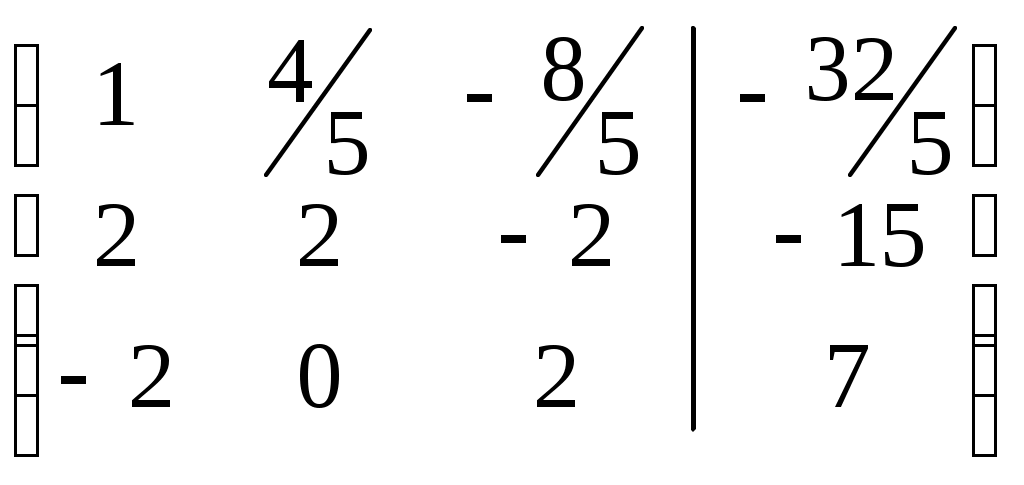
Первую строку умножим на -2 и сложим со второй строкой, результат во второй строке, первую строку умножим на 2 и сложим с третьей строкой, результат в третьей строке.



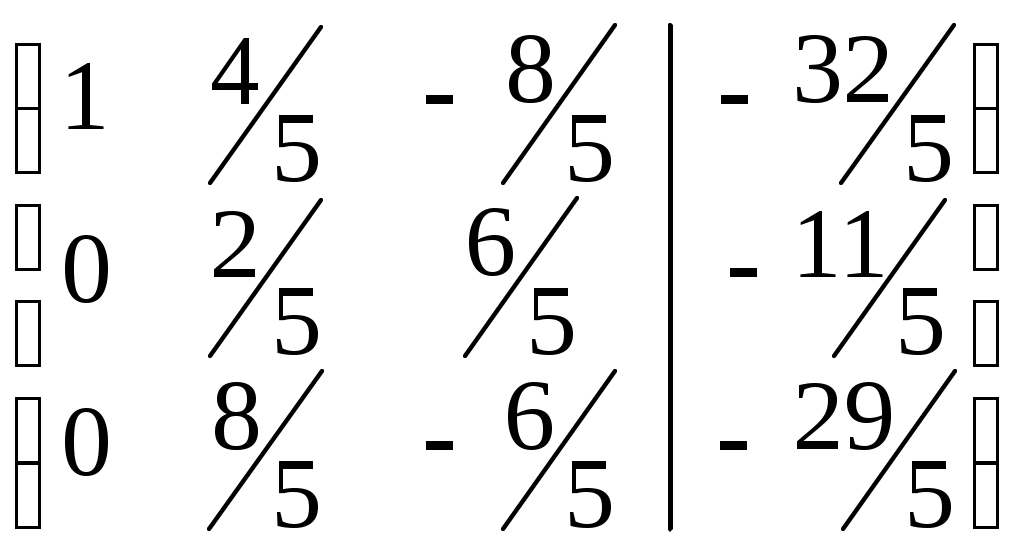
Вторую строку разделим на



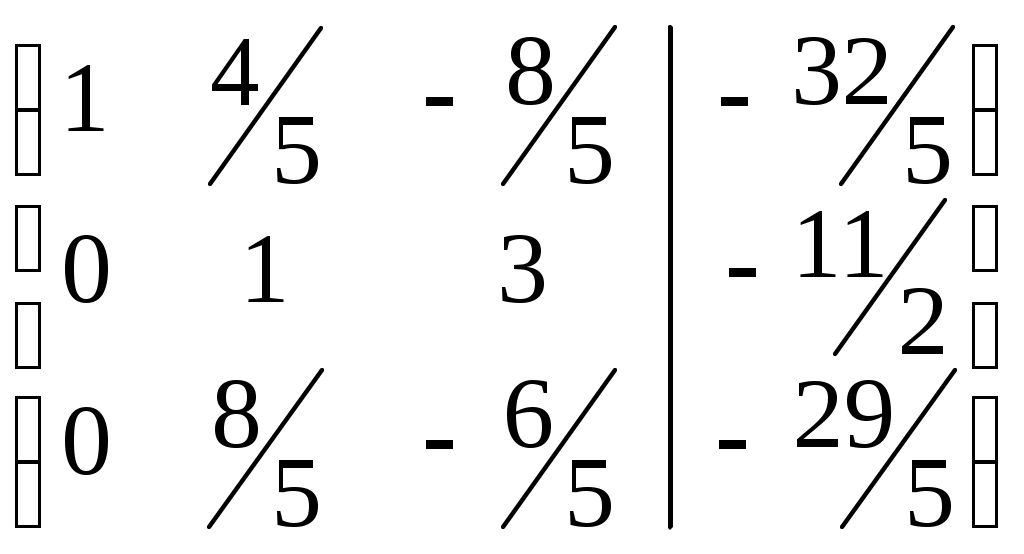
Вторую строку умножим на и сложим с первой строкой

---

, результат в первой строке. Вторую строку умножим на и сложим с третьей строкой, результат в третьей строке.



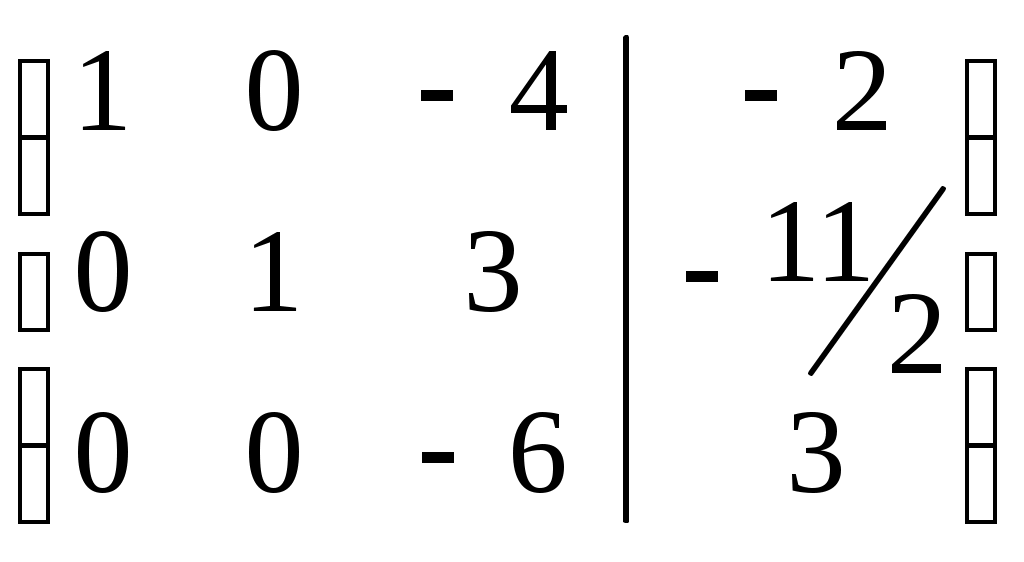
Третью строку разделим на -6:



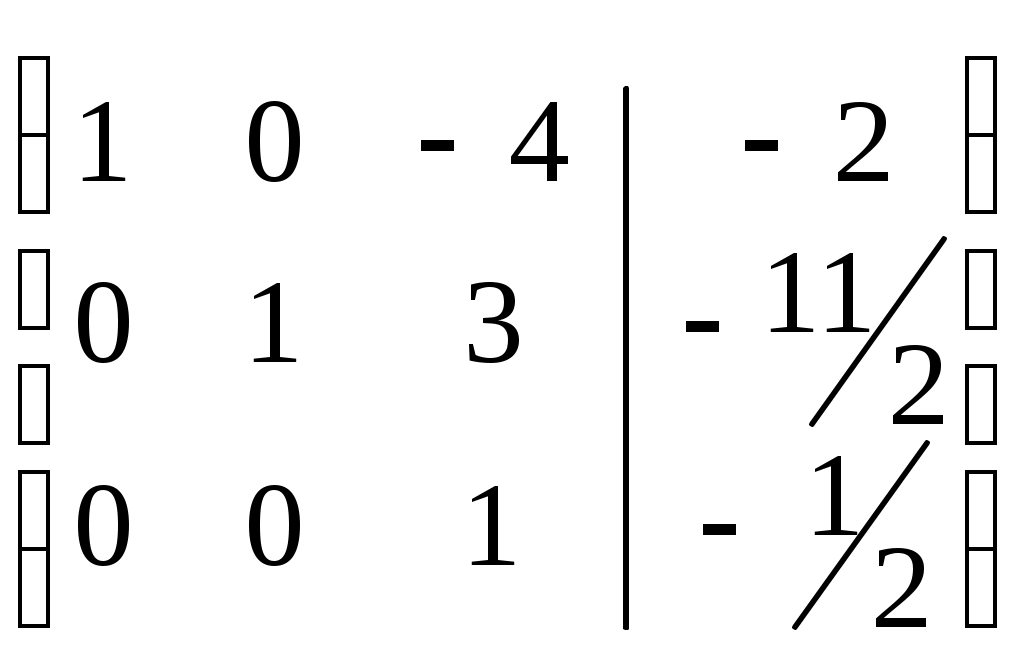
Третью строку умножим на -3 и сложим со второй строкой, результат во второй строке. Третью строку умножим на 4 и сложим с первой строкой, результат в первой строке.


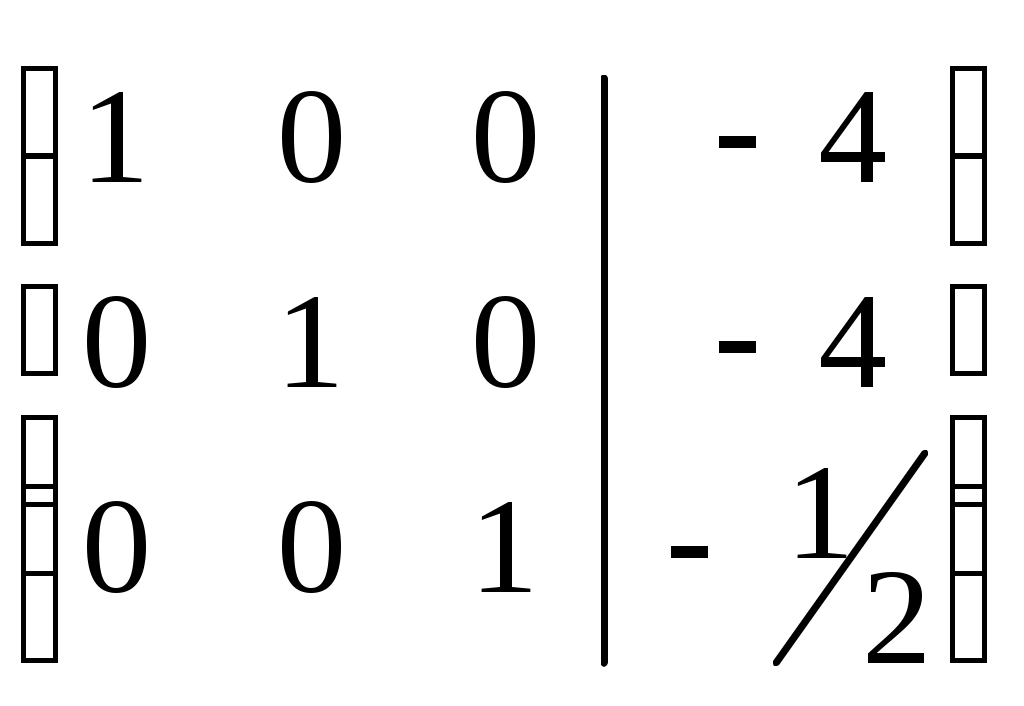
Ответ: .

в) с помощью обратной матрицы:



Решение ищем в виде , откуда .

Вводим обозначения:

, , .

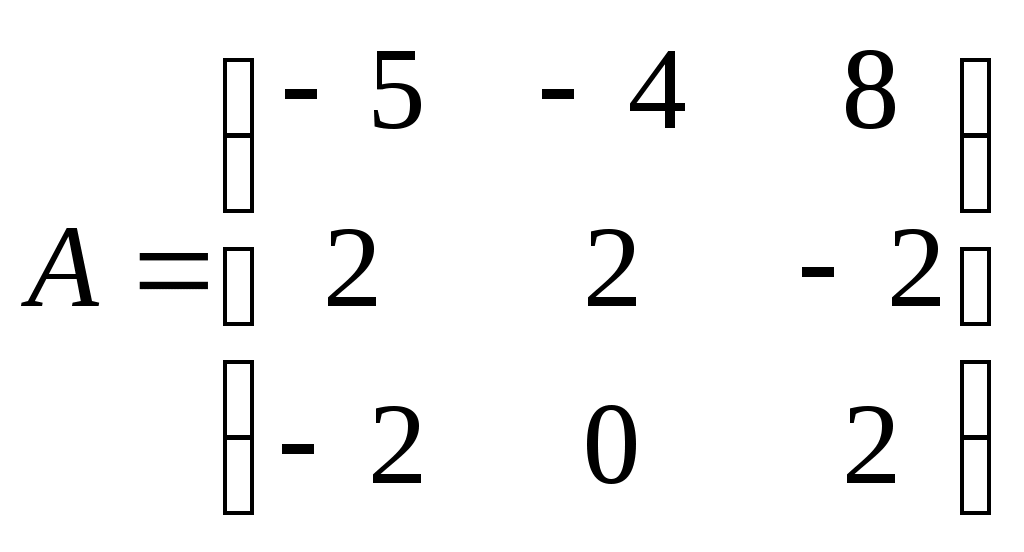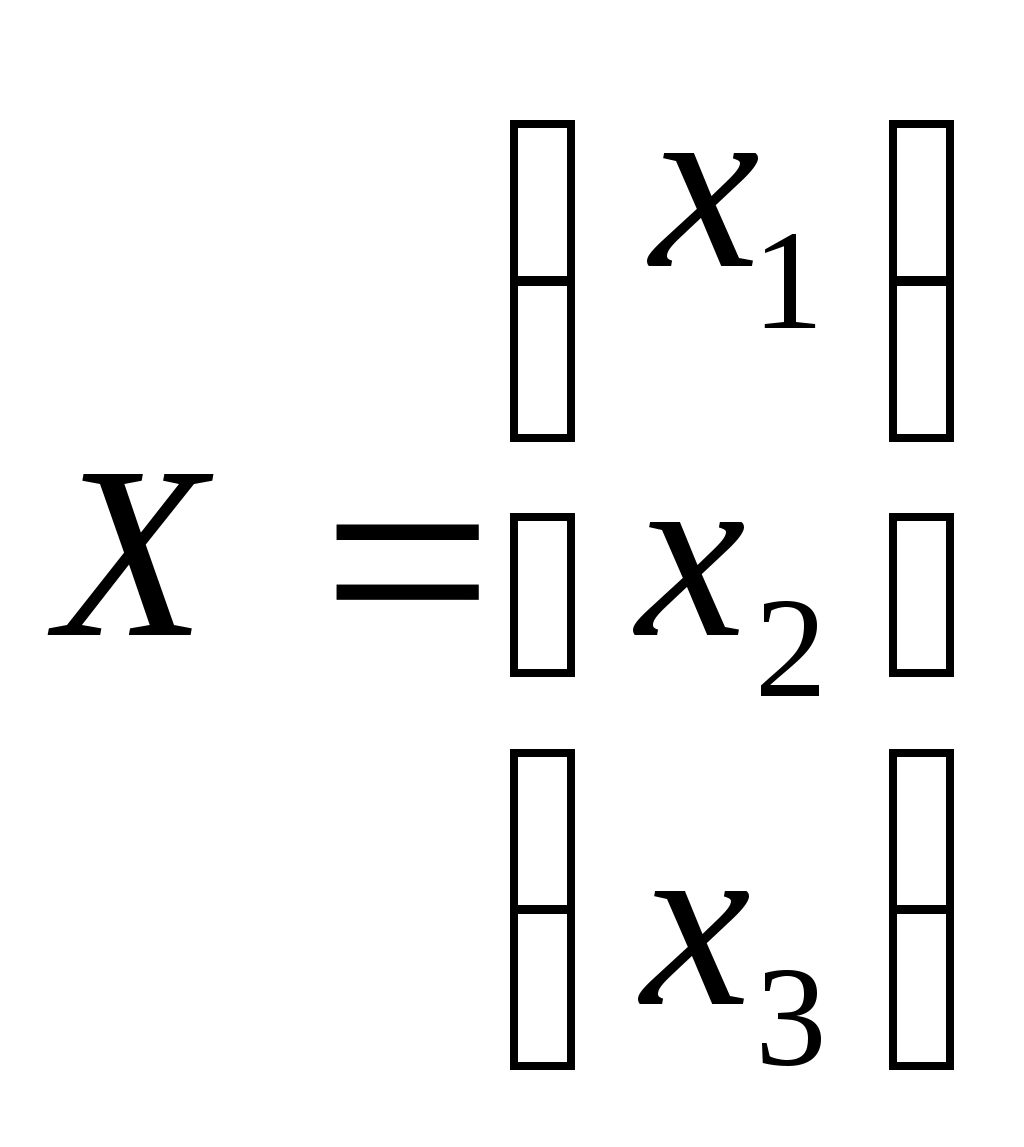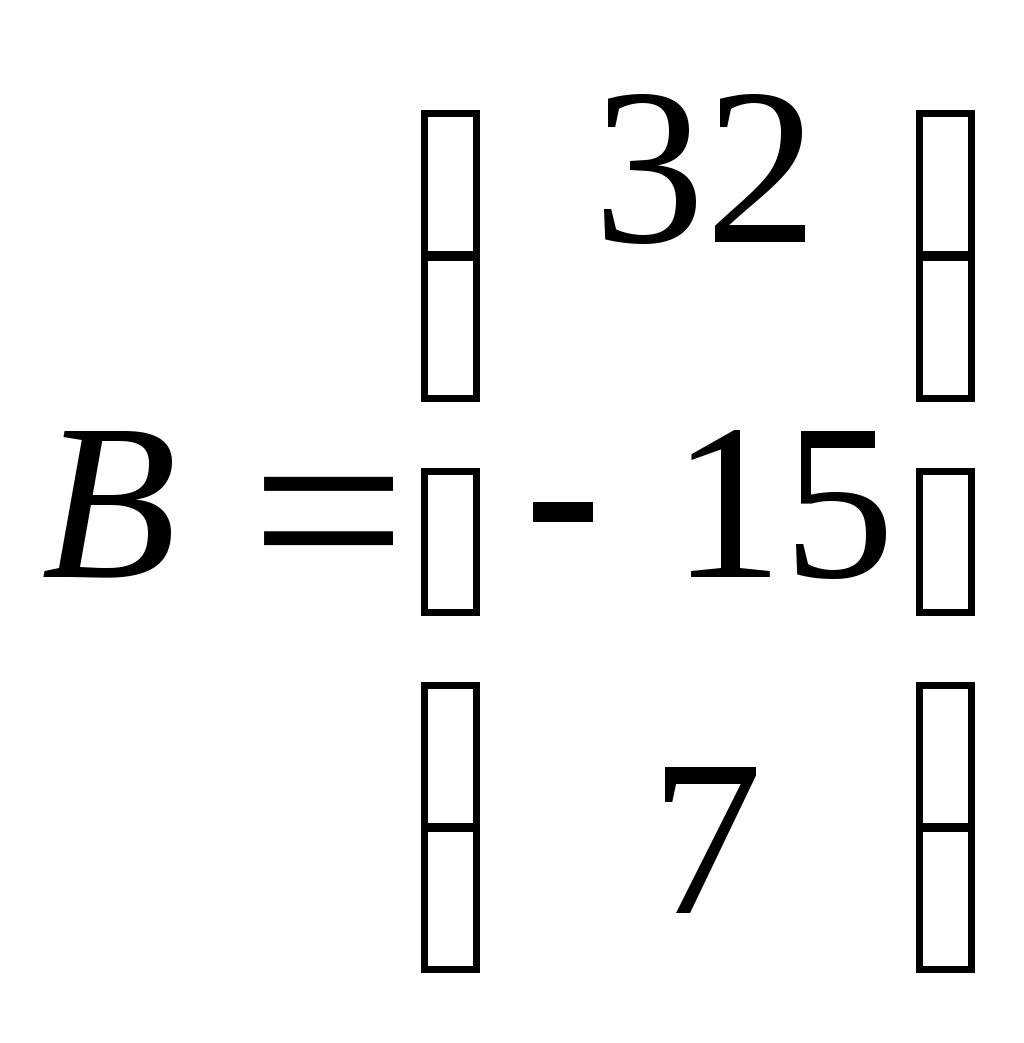Найдём обратную матрицу , для этого найдём алгебраические дополнения:




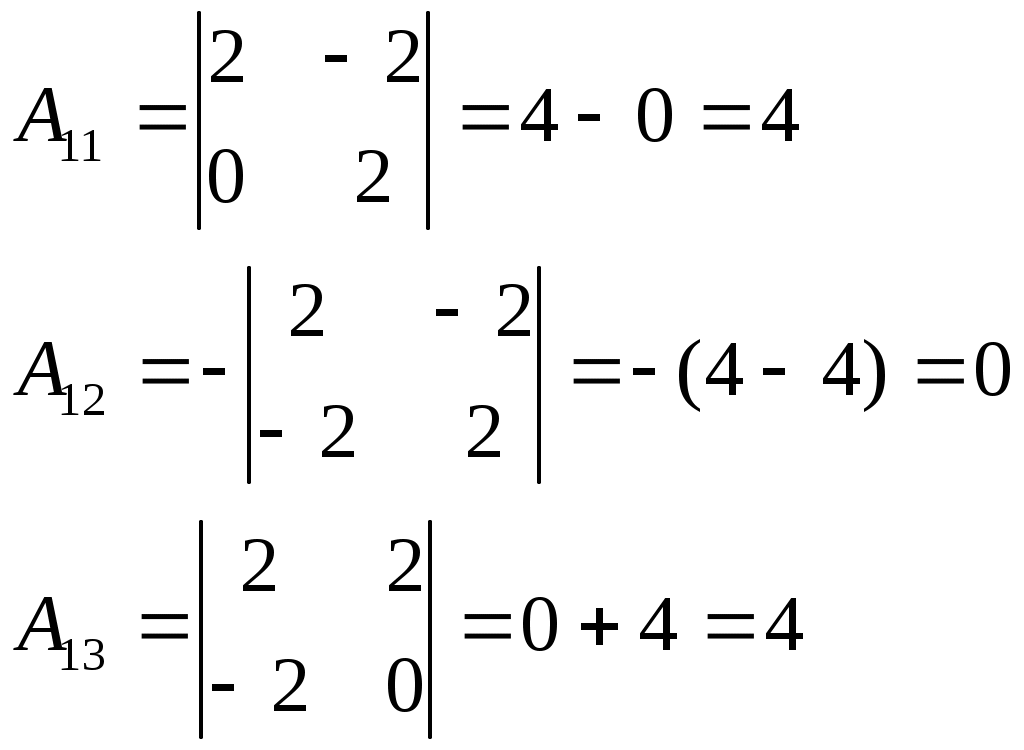
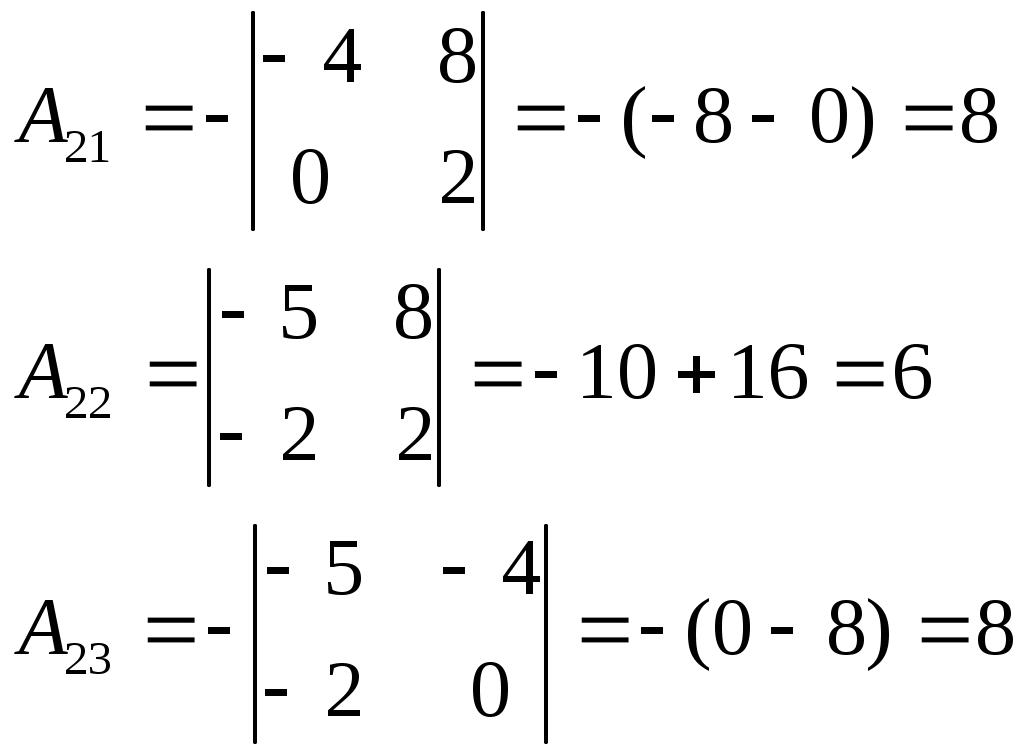
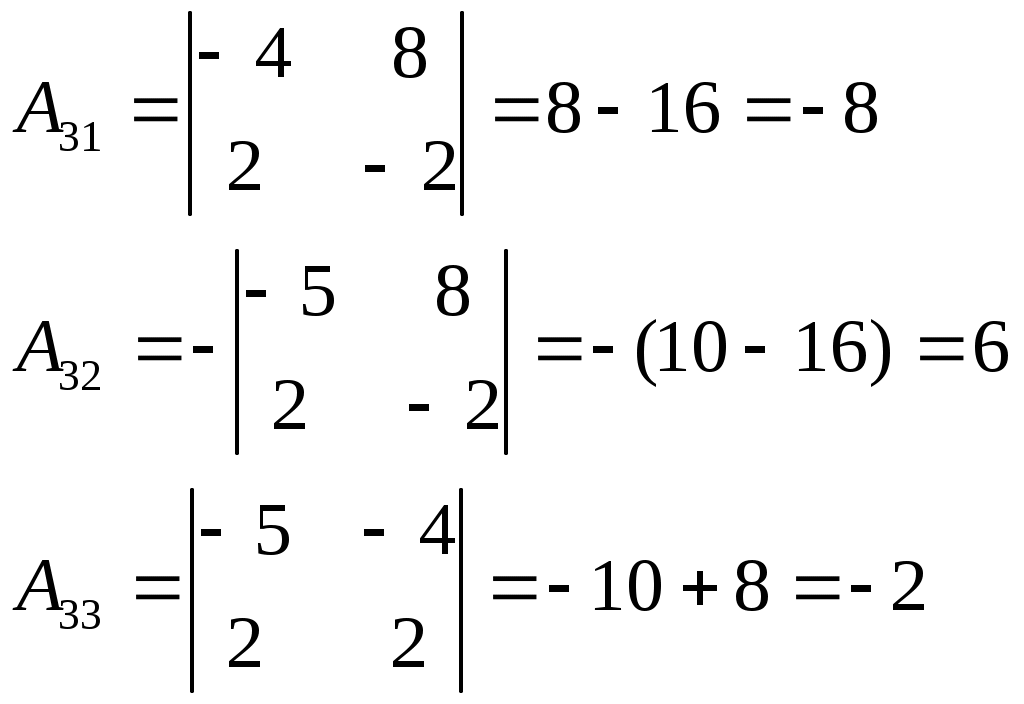
Запишем обратную матрицу:

.

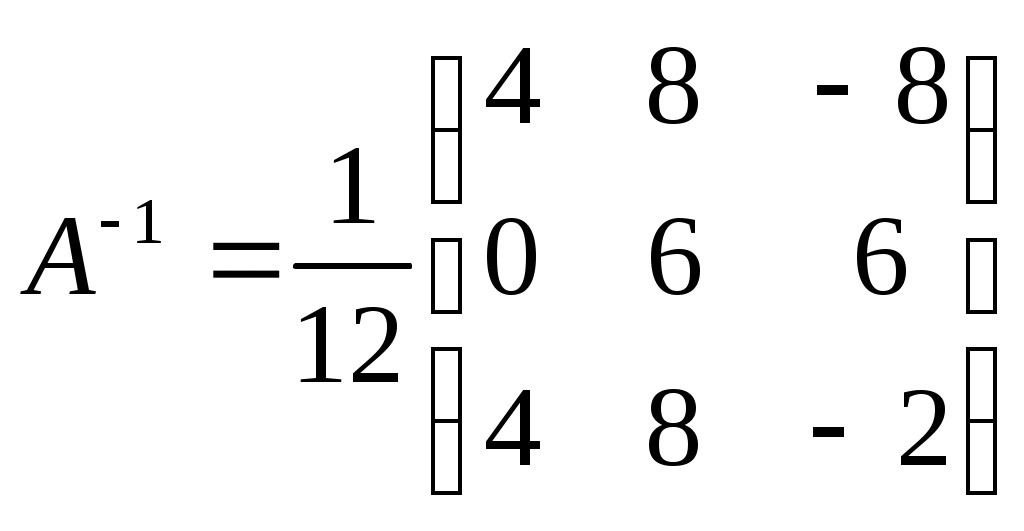Найдём


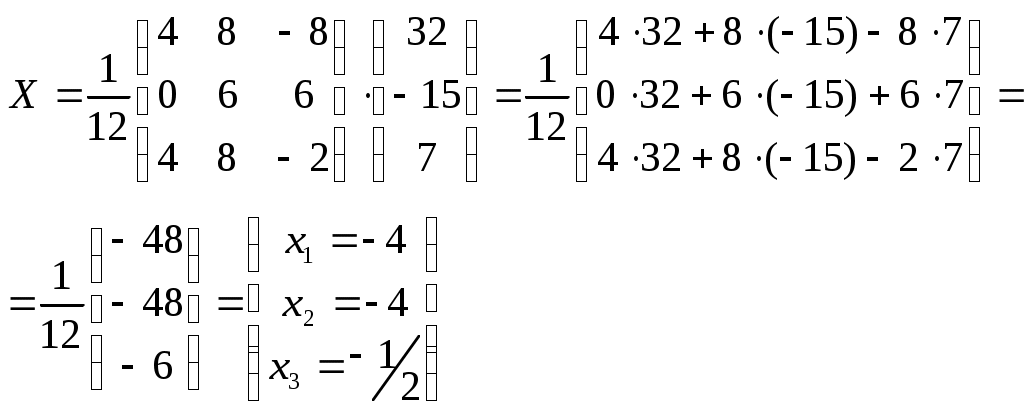
Задание 1.40

Исследовать (по теореме Кронекера - Капелли) совместность и решить систему линейных уравнений.



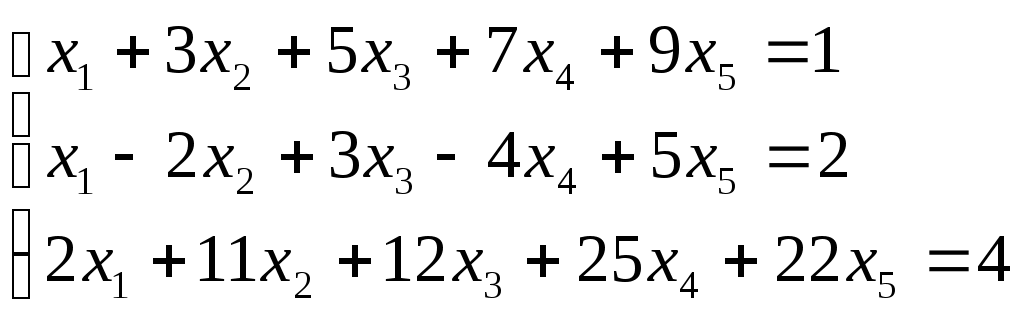
Решение

Теорема Кронекера - Капелли гласит, для того, чтобы система была совместна, необходимо и достаточно

---

, чтобы ранг матрицы А системы равнялся рангу расширенной матрицы В, т.е. Покажем это. Составим расширенную матрицу системы.


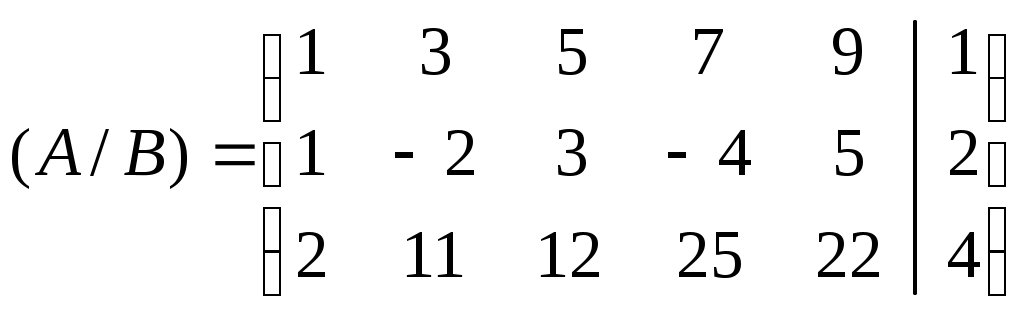
Очевидно, ранг матрицы системы и ранг расширенной матрицы не превосходит числа их строк, т.е. С другой стороны, минор второго порядка, расположенный в верхнем левом углу, отличен от нуля:

т.е. ранг системы

Подвергнем расширенную матрицу следующим преобразованиям: умножим первую строку на (-1) и сложим со второй строкой, запишем во вторую строку. Умножим первую строку на (-2) и сложим с третьей строкой, запишем в третью строку. Тогда матрица преобразования примет вид:



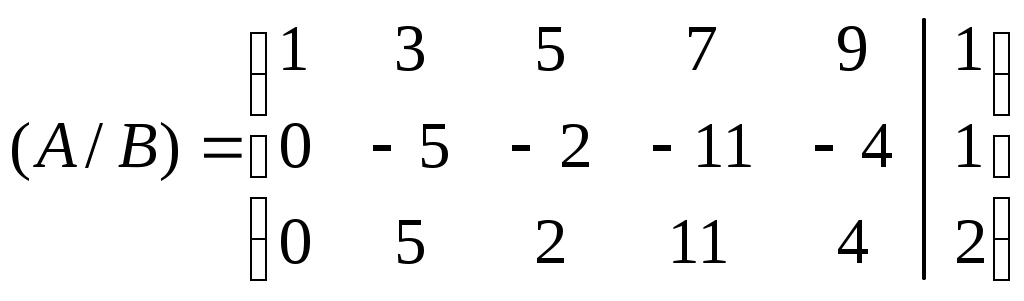
Вторую строку разделим на -5.



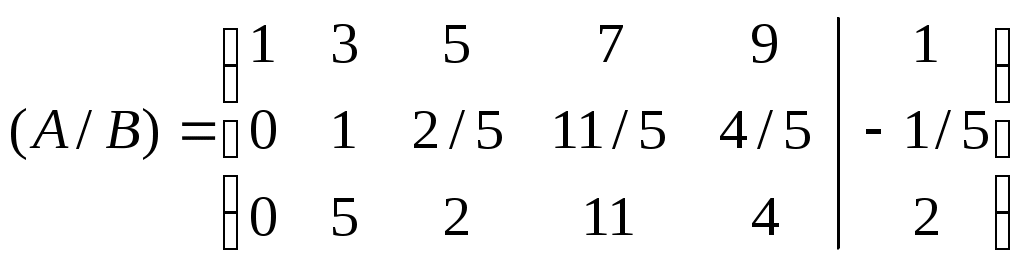
Вторую строку умножим на -3 и сложим с первой строкой, результат в первой строке. Вторую строку умножим на -5 и сложим с третьей строкой, результат в третьей строке.


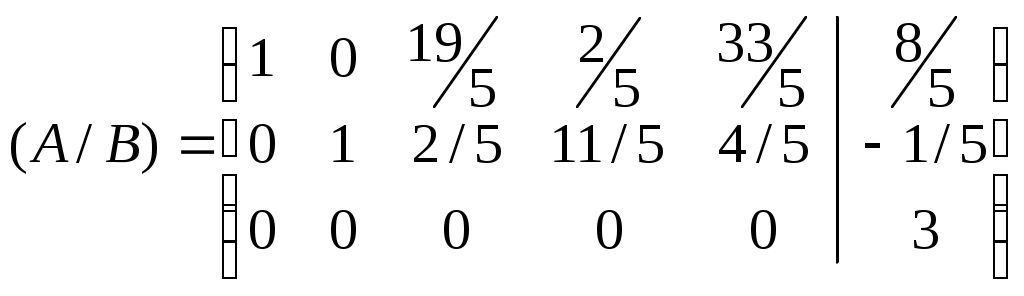
Видим, что ранг расширенной матрицы равен . Смотрим на основную матрицу системы.



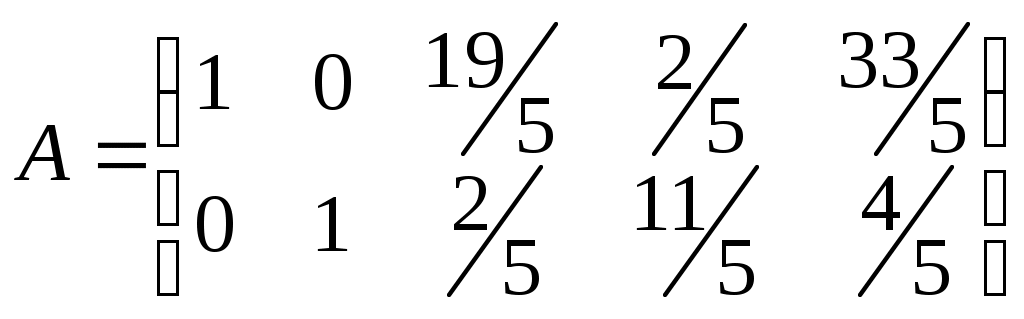
Видим, что определитель минора второго порядка отличен от нуля.



Так как определитель минора второго порядка отличен от нуля, то ранг матрицы А равен 2, т.е. .

Так как , система несовместна.

Следовательно, система не имеет решений.
Задание 1.50

При каких А и В система имеет бесчисленное множество решений? Найти эти решения.

---

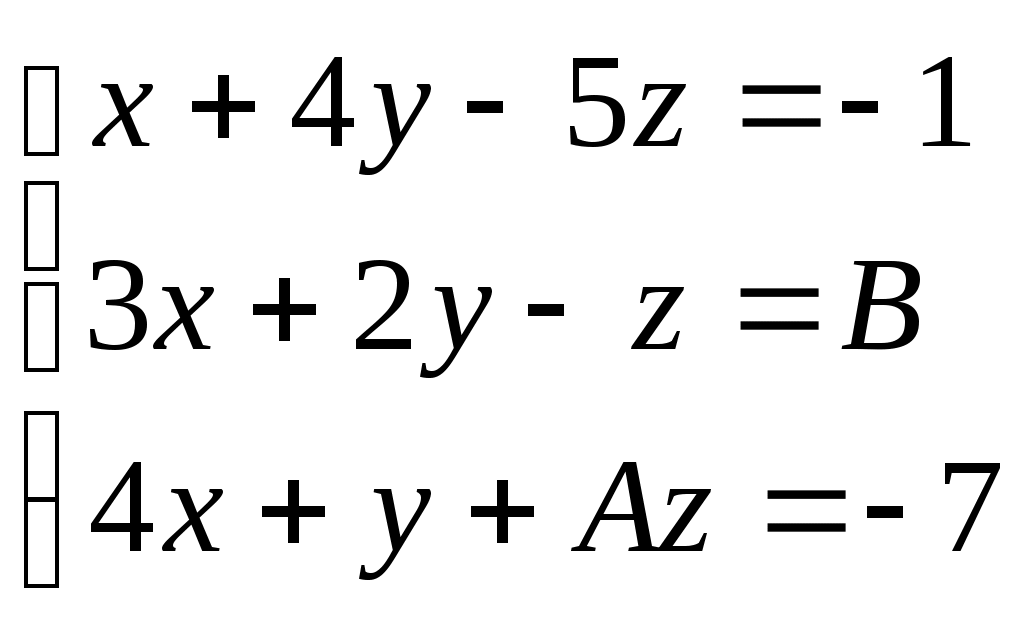
Решение

Система имеет бесчисленное множество решений, когда главный определитель системы равен нулю, но по крайней мере найдётся один элемент, минор которого отличен от нуля.



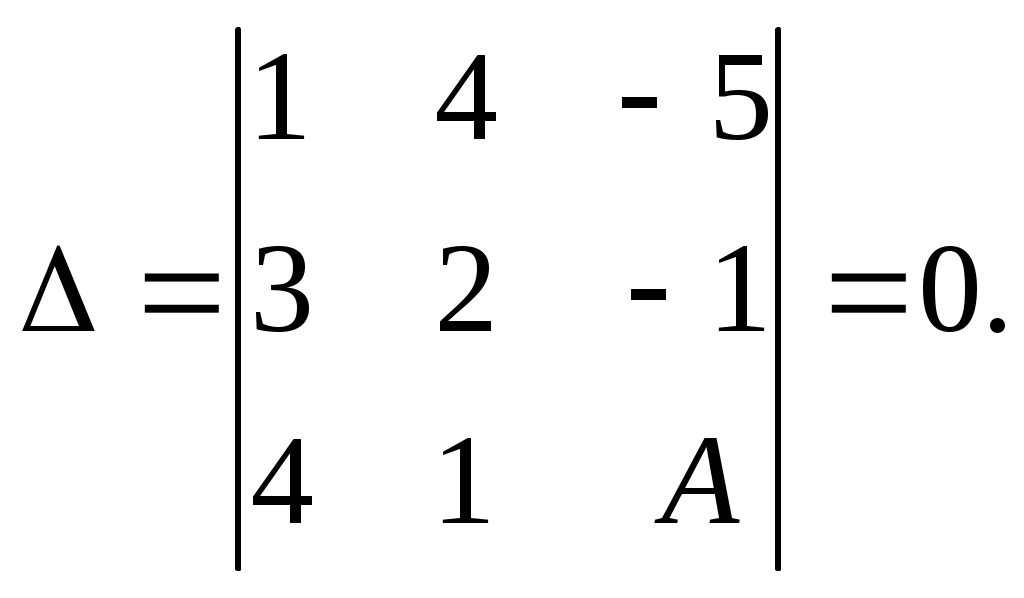
Раскроем данный определитель по элементам первой строки:



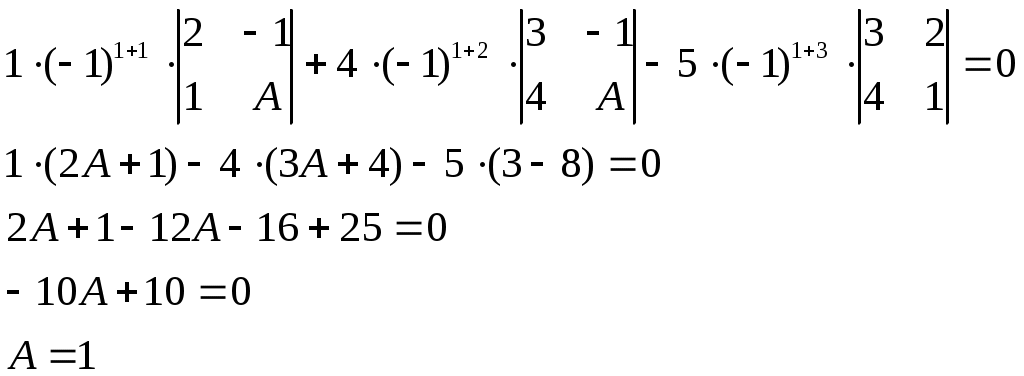
При – главный определитель системы равен нулю.

Запишем расширенную матрицу системы с учётом того, что .



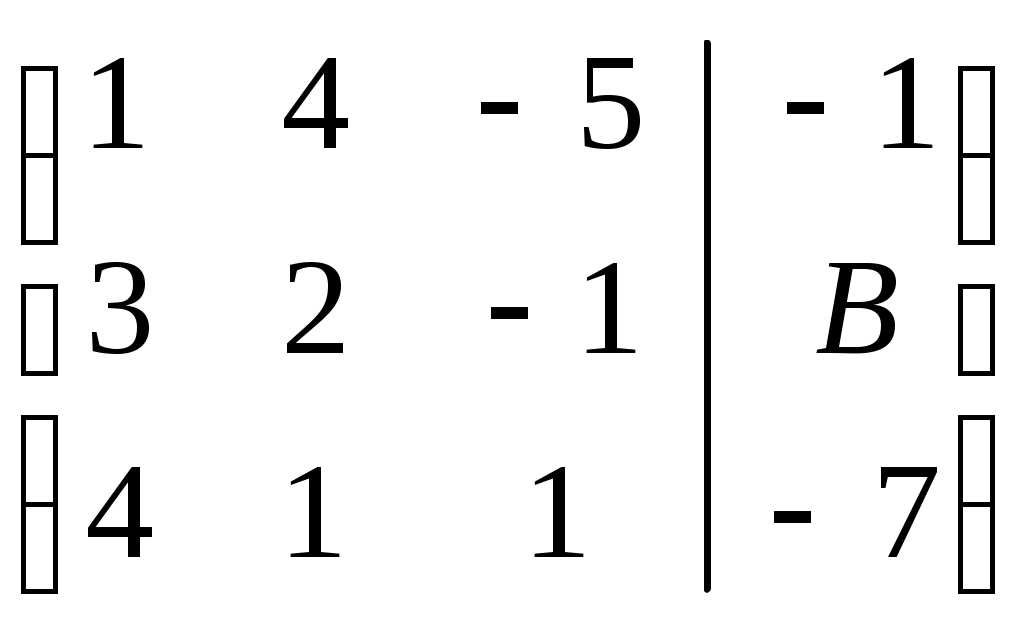
Умножим первую строку на (-3) и сложим со второй строкой, запишем во вторую строку, умножим первую строку на (-4) и сложим с третьей строкой, запишем в третью строку.



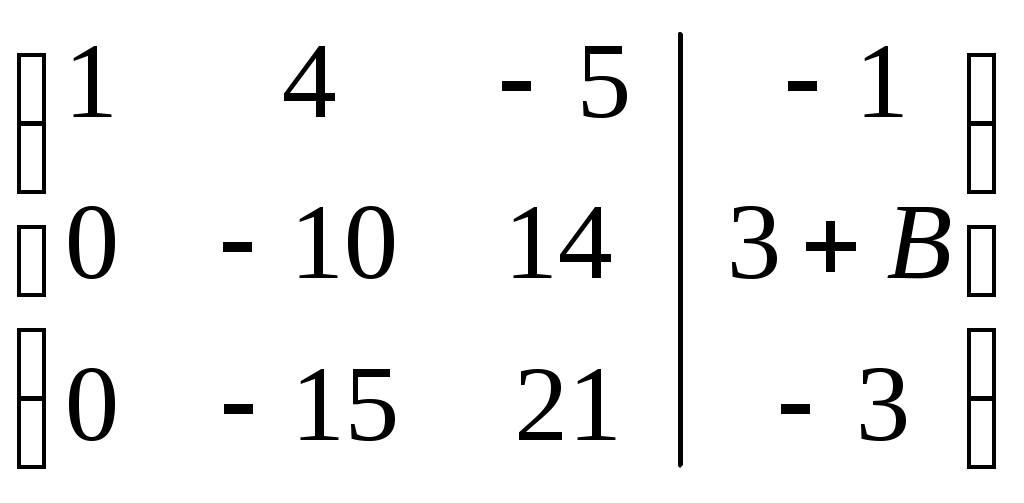
Третью строку раздели на 3:



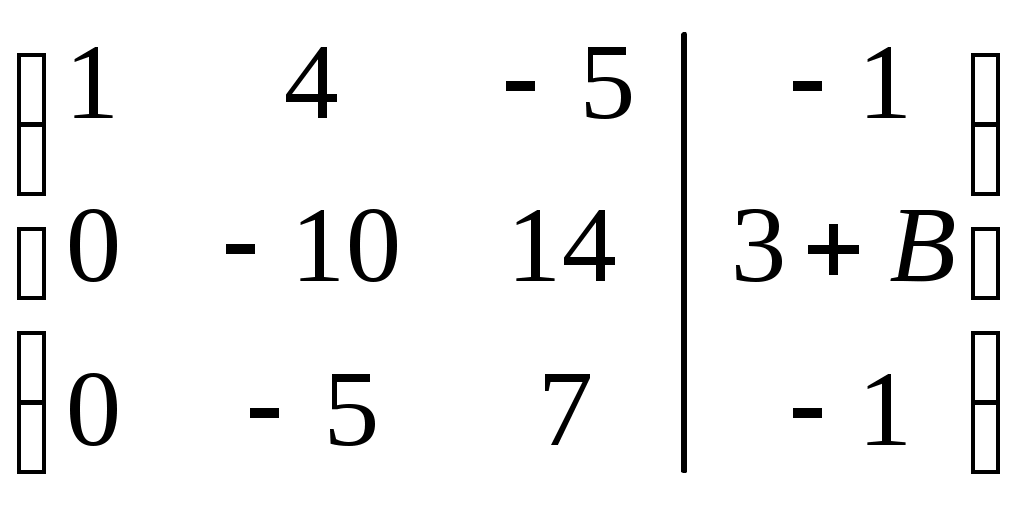
Вторую строку разделим на 2:



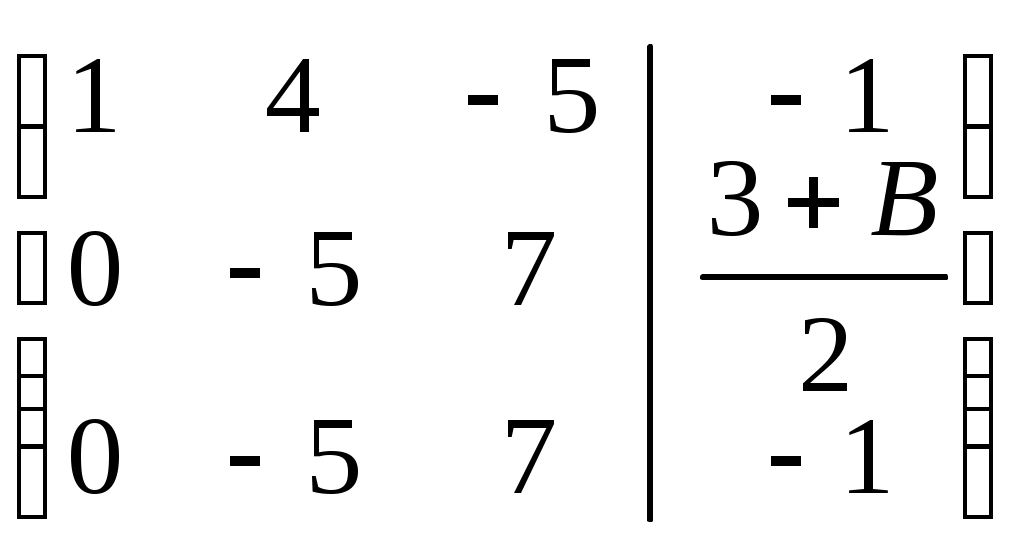
Для того, чтобы система имела бесчисленное множество решений, сделаем так, чтобы вторая и третья строки стали одинаковыми, что мы и сделали.

Найдём В из условия: .

Следовательно, получим матрицу с одинаковой второй и третьей строкой:



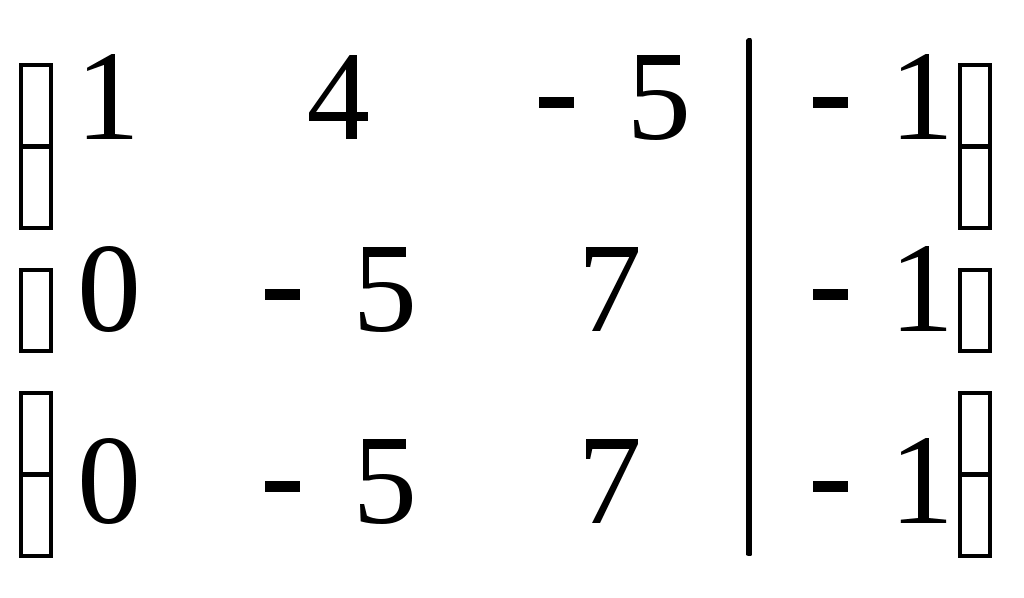
Третью строку убираем:



Обозначим и перенесём в правую часть:


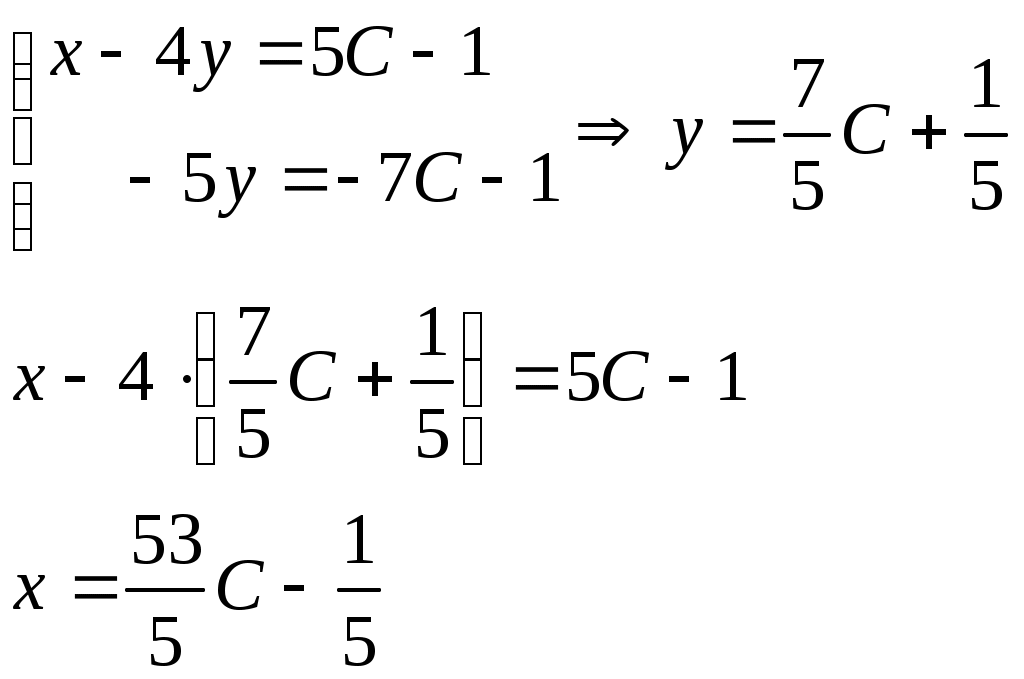
Следовательно, при , система имеет бесчисленное множество решений

любое число.
Задание 1.60

---

Смотрите также файлы

• Тема История и генезис теории управления. Научная теория управления.pdf

• Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области физкультурнооздоровительной деятельности) Дисциплина Родной язык Практическое занятие 2.docx

• Заполните таблицу Каждому из приведенных в ней терминов ниже положений, отмеченных цифрами, найдите соответствующее ему определение из таблицы 2.docx

• Организация Грант Выполнили Студентки группы 2 юр а.pptx

• Современные оздоровительные системы занятий физической культурой и спортом.docx