Файл: Казанский национальный исследовательский технологический университет.docx
Добавлен: 09.11.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Казанский национальный исследовательский технологический университет»
Кафедра теоретических основ теплотехники (ТОТ)
РАСЧЕТНОЕ ЗАДАНИЕ №1
«Смеси Идеальных газов. Термодинамические процессы с идеальными газами»
Вариант №94
Выполнил: студент гр 2311-22
Чибирёв.А.В
Проверил: к.т.н., доц каф ТОТ
Мухамадиев .А.А
Казань 2023
Содержание:
Введение:
Работа посвящена основным понятиям и законам термодинамики. В первой задаче показывается умение работы со смесью идеальных газов, во второй с термодинамическими процессами с идеальным газом.
Идеальным газом называется воображаемый газ, молекулы которого представляют собой материальные точки, объем которых мал по сравнению с объемом, занимаемым газом, и отсутствуют силы взаимодействия.[стр 12]
Рабочим телом тепловых машин часто являются смеси различных газов. Если компоненты смеси не вступают в химическую реакцию друг с другом, и каждый компонент смеси подчиняется уравнению состояния идеального газа, то такая смесь может рассматриваться как некоторый новый идеальный газ, для расчетов с которым необходимо знать его среднюю (кажущуюся) молярную массу или удельную газовую постоянную смеси.
Расчетное определение этих величин возможно, если задан состав смеси. Состав смеси задают объемными (молярными) или массовыми долями.
Каждый компонент смеси ведет себя независимо от других, т.е. занимает весь объем, в котором заключена смесь, и оказывает свое, так называемое парциальное, давления на стенки сосуда. Температура всех компонентов смеси одинакова и равна температуре смеси.
В практических расчетах используется удельная теплоемкость. Удельной теплоемкостью называется количество теплоты, которое необходимо подвести к единице количества вещества, чтобы изменить его температуру на один градус.
В связи с этим определением различают массовые, объемные или молярные удельные теплоемкости. Теплоемкость идеального газа зависит от характера процесса подвода/отвода теплоты, от атомности газа и температуры. Теплоемкость в процессе при постоянном давлении называется изобарной, а в процессе при постоянном объеме – изохорной.
[стр 246-248]
Термодинамический процесс можно наглядно изобразить на P-V и T-S диаграммах.
Задача 1:
Для газовой смеси, заданной объемными долями, требуется определить массовый состав смеси, среднюю (кажущуюся) молекулярную массу смеси через объемные и массовые доли, газовые постоянные компонентов и смеси, плотность смеси при заданных и нормальных условиях, средние мольную, объемную и массовую теплоемкости смеси при р=const и v=const в интервале температур от t1 до t2, а также затраты тепла на нагрев при р=const 10нм3 и 10кг смеси в интервале температур от t1 до t2. Зависимость теплоемкости от температуры считать нелинейной.
Дано: r(CO2)=0.14; r(N2)=0.77; r(H2O)=0.05 ; r(O2)=0.04 ; P=0.55 МПа ; t1=50°С; t2=410°С ; V=10нм3 ; M=10кг
Найти: gi -? ; μсмеси - ? ; Ri - ?; Rсм - ?; ρ - ?; ρн.у.- ?; сp - ?; μсp - ?; сp’ - ?; сv - ?; μсv - ?; сv’ - ?; q - ?;
Решение:
Массовые доли компонентов можно определить по формуле перехода:
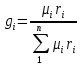 [стр 17] где
[стр 17] где 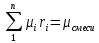 ,
, 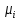 - молярная масса компонента смеси,
- молярная масса компонента смеси,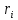 -объемная доля компонента смеси
-объемная доля компонента смеси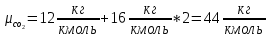 ;
; 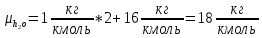 ;
; 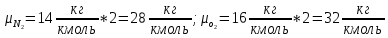
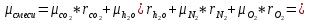
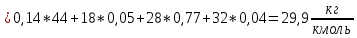
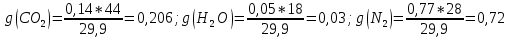
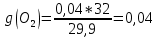
Через массовые доли среднюю (кажущуюся) молекулярную массу смеси определяют по формуле:
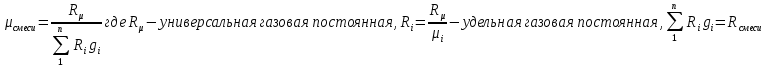 [ стр 13,17-18]
[ стр 13,17-18]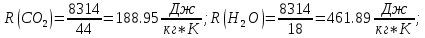
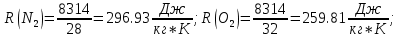
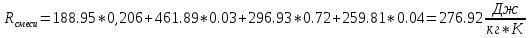
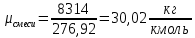
Плотность смеси определяют по уравнению состояния идеального газа:
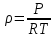 [стр 14]
[стр 14]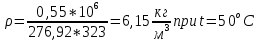
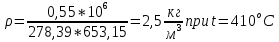
При физических нормальных условиях T=273K , P=101325 Па
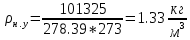
Из справочной таблицы выписываем средние изобарные мольные теплоемкости [стр11] :
| t2 Co | Азот N2 | Кислород O2 | Углекислый газ CO2 | Водяной пар H2O |
| 0 | 29.115 | 29.274 | 35.860 | 33.499 |
| 100 | 29.144 | 29.538 | 38.112 | 33.741 |
| 200 | 29.228 | 29.931 | 40.059 | 34.118 |
| 300 | 29.383 | 30.400 | 41.755 | 34.575 |
| 400 | 29.601 | 30.878 | 43.250 | 35.090 |
| 500 | 29.864 | 31.334 | 44.573 | 35.630 |
Средние изобарные мольные теплоемкости при заданных температурах находим методом интерполяции:
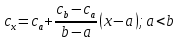
Для t1=40oC
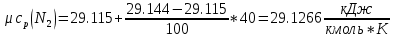
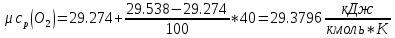
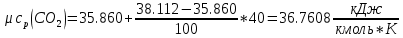
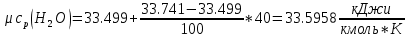
Для t2=380oC
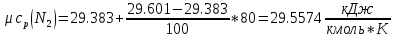
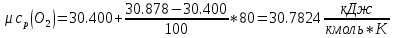
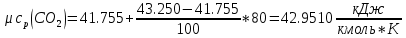
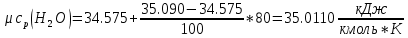
Средняя теплоемкость находится по формуле:
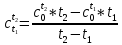 [стр 38]
[стр 38]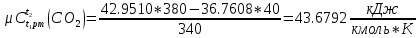
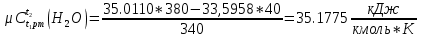
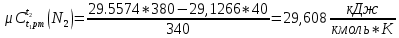
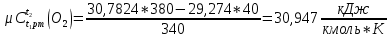
Мольная теплоемкость смеси находится по формуле:
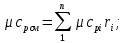 [стр 41]
[стр 41]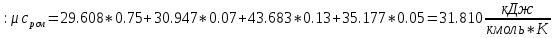
Массовую теплоемкость находим из соотношения:
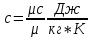 [стр 34]
[стр 34]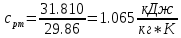
Объемная теплоемкость находится из соотношения:
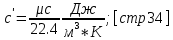
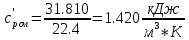
Мольную изохорную теплоемкость можно найти из уравнения:
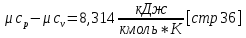
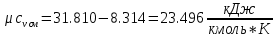
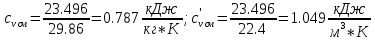
Количество теплоты находится по уравнению:
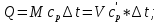
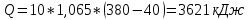
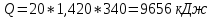
Задача 2:
Газ массой m имеет начальные параметры – давление P1 и температуру t1. После политропного изменения состояния параметра газа стали P2 и V2. Определить характер процесса (сжатие или расширение), конечную температуру t2, показатель политропы n, теплоемкость процесса С, работу, тепло, изменение внутренней энергии, энтальпии и энтропии. Определить эти же параметры, а также конечное давление P2, если изменение состояния до того же конечного объема V2 происходит: а) по адиабате; б) по изотерме. Изобразить (без расчета) все процессы в PV и TS диаграммах. Составить сводную таблицу результатов расчета. Теплоемкость газа считать постоянной.
Дано: СО2 ; t1=200°С ; P1=6.0 бар; m=10.5 кг; P2=1.5 бар; V2=0.85 м3
Найти: характер процесса – ? ; t2 – ? ; n – ? ; с – ? ; L – ? ; Q – ? ; ∆U – ? ; ∆H – ? ; ∆S – ? ; P2 – ?
Решение: По уравнению состояния идеального газа определяем начальный объем:
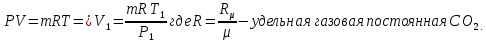
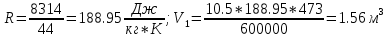
V1>V2 , значит происходит процесс сжатия газа.
Показатель политропы определяется через связь между параметрами состояния:
 [стр 60]
[стр 60]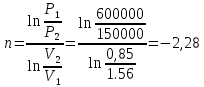
Температуру t2 определяют по формуле:
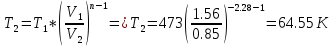 [стр 60]
[стр 60]Теплоемкость политропного процесса определяется по формуле:
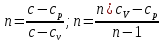
По таблице теплоемкости для многоатомного газа [стр 11]
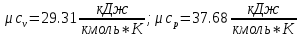
Связь между молярной и массовой теплоемкостью: