ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 197
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Законы склеивания:
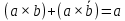
| ???? | b | 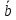 |  | 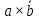 | 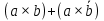 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
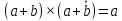
| ???? | b | 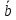 |  | 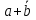 | 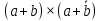 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
-
Законы де Моргана:
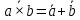
| ???? | b |  |  |  | 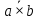 | 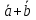 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
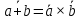
| ???? | b |  |  |  | 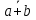 | 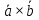 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
Задание №3:
Из заданных логических функций тождественно истинной являются:
Решение:
| № | Функция АЛ | Логическое выражение | Закон АЛ | =1 |
| 1 | A или А или А | 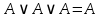 | идемпотентности | нет |
| 2 | А или не А |  | дополнительности | да |
| 3 | А или А или не А | 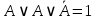 | дополнительности и идемпотентности | да |
| 4 | А и А и А | 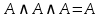 | идемпотентности | нет |
| 5 | А и не А | 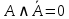 | идемпотентности | нет |
| 6 | А и А и не А | 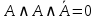 | дополнительности и идемпотентности | нет |
| 7 | А или не А или не А | 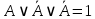 | дополнительности и идемпотентности | да |
| 8 | А и не А и не А | 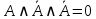 | дополнительности и идемпотентности | нет |
| 9 | А и не А или не А | 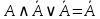 | дополнительности и идемпотентности | нет |
| 10 | А или А и не А | 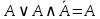 | Поглощения и идемпотентности | нет |
| 11 | А или не А и А | 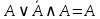 | Поглощения и идемпотентности | нет |
| 12 | А или не А или А | 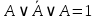 | Дистрибутивный и дополнительности | да |
| 13 | А и не В или А | 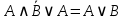 | Поглощения | нет |
| 14 | А и не А или В | 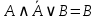 | Дополнительности и универсального множества | нет |
| 15 | А и В или не А | 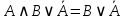 | Поглощение | нет |
| 16 | А или В или не А | 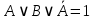 | Дополнительности и универсального множества | да |
| 17 | не А и не В или А | 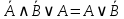 | Поглощение | нет |
| 18 | не А или В или не В | 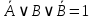 | Дополнительность и универсальное множество | да |
Задание №4
Для словесного описания функции: «Логическое выражение является истинным, если хотя бы два из трёх высказываний, составляющих данное выражение, являются истинными» записать:
Решение:
• таблицу истинности
• совершенную дизъюнктивную и конъюнктивную формы функции
| X1 | X2 | X3 | y=f(x1 ;x2 ;x3) | CДНФ | СКНФ |
| 0 | 0 | 0 | 0 | - | 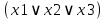 |
| 0 | 0 | 1 | 0 | - | 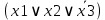 |
| 0 | 1 | 0 | 0 | - | 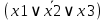 |
| 0 | 1 | 1 | 1 | 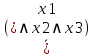 | - |
| 1 | 0 | 0 | 0 | - | 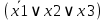 |
| 1 | 0 | 1 | 1 | 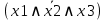 | - |
| 1 | 1 | 0 | 1 | 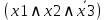 | - |
| 1 | 1 | 1 | 1 | 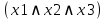 | - |
CДНФ:
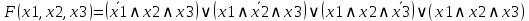
CКНФ:
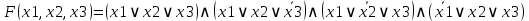
• минимальную дизъюнктивную и конъюнктивную формы функции с использованием метода непосредственных преобразований.
Минимизация СДНФ:
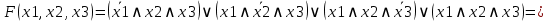
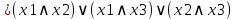
Минимизация СКНФ:
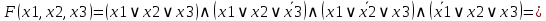
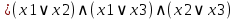
Ответы на контрольные вопросы к практической работе:
-
Что такое алгебра логики? Что называют логической функцией?
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Логическая функция - это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием, которое называется значением функции.
2) Какими способами можно описать логическую функцию?
Словесный способ. Здесь все случаи, при которых функция принимает значения 0 или 1, описываются словесно. Так, функцию «ИЛИ» со многими аргументами можно описать следующим образом: функция принимает значение 1, если хотя бы один из аргументов принимает значение 1, иначе значение функции равна 0.
Табличный способ. Булева функция задается в виде таблицы истинности. В левой части таблицы истинности записываются все возможные n-разрядные двоичные комбинации аргументов ,а в правой – значения функции на этих наборах. Таблица истинности содержит 2n строк.
Числовой способ. Функция задается в виде последовательности десятичных эквивалентов тех наборов аргументов, на которых функция принимает значение 1. Например, двоичные наборы 010 и 101 имеют десятичные номера 2 и 5 соответственно.