Файл: Лабораторная работа 23 Изучение законов прямолинейного движения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 157
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 23
Изучение законов прямолинейного движения
Цель работы: проверка уравнений кинематики и динамики прямолинейного движения с помощью машины Атвуда.
Приборы и принадлежности: машина Атвуда, секундомер, линейка.
Краткая теория
1. На каждый груз, подвешенный к нити, действуют две силы – сила тяжести и сила натяжения нити, под действием которых грузы движутся (рис. 2). Если нити и блок невесомы, сама нить нерастяжима, а сила трения в блоке мала, то ускорения обоих грузов будут одинаковы по величине и противоположны по направлению, а натяжение нити одинаково и справа и слева от блока.
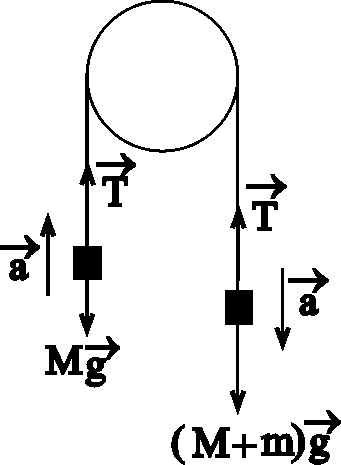 Рис. 2. Блок с грузами и перегрузком |
 . (1)
. (1)Для груза без перегрузка:
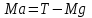 , (2)
, (2)где
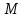 – масса груза,
– масса груза,  – масса перегрузка,
– масса перегрузка,  – ускорение грузов,
– ускорение грузов,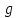 – ускорение свободного падения,
– ускорение свободного падения,  – сила натяжения нити.
– сила натяжения нити.Решая совместно уравнения (1) и (2), получим теоретическое значение ускорения:
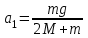 . (3)
. (3)Ускорение равноускоренного движения можно также найти из уравнения кинематики
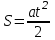 , (4)
, (4)где
 – путь, пройденный грузами,
– путь, пройденный грузами,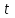 – время движения грузов.
– время движения грузов.Таким образом, зная пройденный путь и время движения, можно определить экспериментальное значение ускорения:
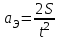 . (5)
. (5)2. Равенство (3) справедливо, если блок считать невесомым. Более точное значение ускорения
 можно получить, если учесть массу вращающегося блока.
можно получить, если учесть массу вращающегося блока.Груз с перегрузком будет двигаться вниз с ускорением
 под действием силы тяжести
под действием силы тяжести  и силы натяжения нити
и силы натяжения нити 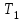 :
: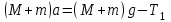 . (6)
. (6)Груз без перегрузка движется вверх с тем же ускорением
 под действием силы тяжести
под действием силы тяжести  и силы натяжения нити
и силы натяжения нити 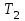 :
: 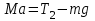 . (7)
. (7)Нить будет натянута по обе стороны блока по-разному, и разность сил натяжения нитей
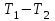 будет создавать момент сил, вращающий блок. Применяя основной закон динамики вращательного движения тела, получим:
будет создавать момент сил, вращающий блок. Применяя основной закон динамики вращательного движения тела, получим: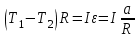 , (8)
, (8)где
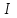 – момент инерции блока
– момент инерции блока  – т.к. блок не сплошной,
– т.к. блок не сплошной,  – масса блока.
– масса блока.Решая совместно уравнения (6-8), получим:
 , (9)
, (9)где
 –масса груза,
–масса груза,  г,
г,
– масса перегрузка,
 – масса блока;
– масса блока;  =10,2 г.
=10,2 г.Таблица 1. Массы перезрузков
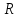 , м , м | 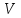 , м3 , м3 |  , кг , кг |
| 4.8× 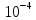 | 463×  | 3.6× 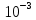 |
| 6.2× 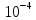 | 998×  | 7.9× 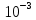 |
Таблица 2. Прямые измерения
 , кг , кг |  , м , м | 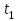 , с , с | 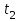 , с , с |  , с , с | 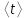 , с , с |
| 3.6× 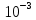 | 0.35 | 1.44 | 1.41 | 1.42 | 1.42 |
| 7.9× 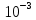 | 0.39 | 2.11 | 2.14 | 2.10 | 2.12 |
Таблица 3. Косвенные измерения.
 , кг , кг | 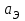 , м/с2 , м/с2 | 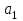 , м/с2 , м/с2 |  , м/с2 , м/с2 |  , % , % | 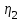 , % , % |
| 3.6×  | 0.35 | 0.22 | 0.21 | 59 | 66 |
| 7.9×  | 0.17 | 0.49 | 0.46 | 65 | 63 |