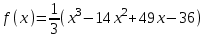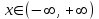
Задание 2Исследовать функцию и построить ее график.Решение:1) Данная функция существует при любых значениях x: 2)Т.к. область определения функции симметрична относительно начала координат, то проверим функцию на чётность (нечётность), для этого составим 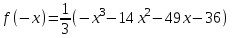. Поскольку не выполняется ни равенство 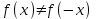, ни 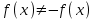, то данная функция – общего вида3)Найдем точки пересечения графика функции с осями координат. Чтобы найти точки пересечения с OX , решим уравнение 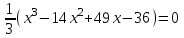. Выпишем целые делители свободного члена уравнения 12: 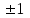, , 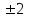, , 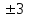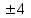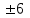.Из них подбором найдем первый корень уравнения: 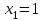: 1-14+49-36=0. Далее используем теорему Безу: если 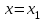корень многочлена n-ой степени 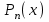, то его можно представить в ви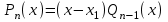де: , где 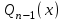– многочлен степени n −1. В нашем случае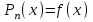 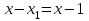, чтобы найти 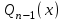, разделим f(x) на x −1.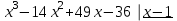

---

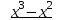
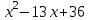
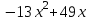
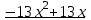
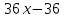
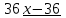
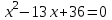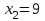
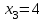
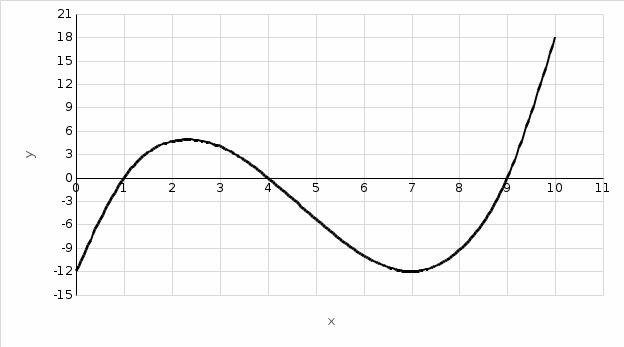
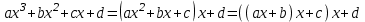
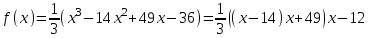
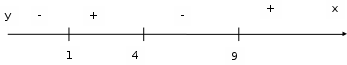
0Чтобы найти другие корни, решим уравнение , его корни Итак, график функции пересекает OX при х=1, х=4, х=9. Ось ординат OY график пересекает при у=f(0)=-36 4) определим промежутки знакопостоянства функции:Для этого нанесем на числовую ось нули функции и определим знак функции в полученных интервалах. При вычислении значений функции удобно использовать формулу5)Исследуем наличие асимптот. 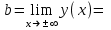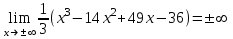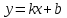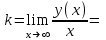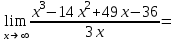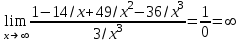Составим пределы: а) для горизонтальной асимптотыб) для наклонной асимптотыТ.к. составленные пределы равны +∞ или -∞ , то ни горизонтальной, ни наклонной асимптот нет. Вертикальных асимптот нет, т.к. функция не имеет точек разрыва и везде существует.6) найдем промежутки возрастания и убывания и исследуем на наличие точек экстремума: Для этого найдем производную функции 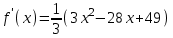и её критические точки из условия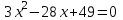D=784-4*3*49=196

---

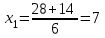
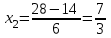
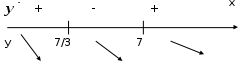
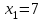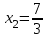
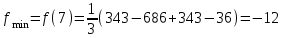
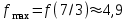
- точка минимума- точка максимума7) найдем промежутки выпуклости и вогнутости и точки перегиба/ Из условия 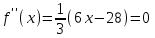( найдем критическую точку x = 14/3) . Нанесем ее на числовую ось и определим знак второй производной, по которому определим промежутки выпуклости и вогнутости.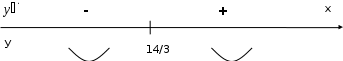 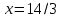- точка перегиба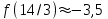Отметив характерные точки: экстремумы, точки пересечения с осями координат, строим график функции (приведён на рисунке справа)Задание 2.Окно имеет форму прямоугольника, завершённого полукругом. Периметр окна равен 14м. Каковы должны быть размеры окна, чтобы оно пропускало наибольшее количество света?Решение:

Обозначим R - радиус круга, b - высоту прямоугольника. Тогда периметр и площадь равны 

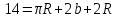
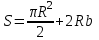
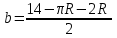
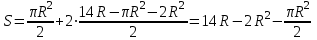
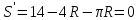
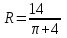
из первого уравнения выразим b:подставим во второе:найдем производную и приравняем к нулю:Решая уравнениеТак как при 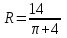вторая производная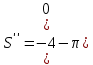 то при 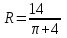площадь будет максимальной.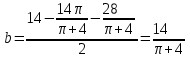

---

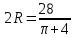
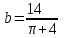
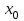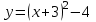
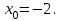
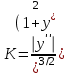
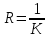
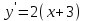
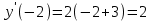
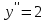
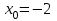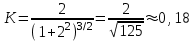
стороны прямоугольника: х=у=Задание 3.Найти кривизну, радиус кривизны линии у=у(х) в точке с абсциссой . Значение кривизны и радиус указать с точностью до 0,01.Решение:формула для кривизны: формула для радиуса: кривизна в точке :радиус кривизны в точке :

---

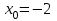Смотрите также файлы

• Тема Расследование и учет несчастных случаев на производстве Цель занятия.doc

• Практических заданий по дисциплине этика делового общения.docx

• Основой кадровой политики компании Asstra ag являются следующие принципы.docx

• Оформление курсовой работы.pdf

• Контрольная работа 8 класс 1 вариант слово Информатика.docx