Практическое занятиеРабота с таблицами истинности и функциональными схемамиЦель занятия:

• 
  учить составлять таблицы истинности для логических функций;
  
• 
  учить строить функциональной схемы по логической формуле;
  
• 
  учить составлять логическую формулу по функциональной схеме.
  

Пояснение к работе.Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Буль первым показал, что существует аналогия между алгебраическими и логическими действиями, так как и те, и другие предполагают лишь два варианта ответов – истина или ложь, нуль или единица.На основе анализа логической связи между высказываниями делается логический вывод. Для получения логического вывода составляется  таблица истинности, в которой записывают все возможные комбинации каждого простого высказывания.Работа ЭВМ как автоматических устройств основана исключи­тельно на математически строгих правилах выполнения команд, программ и интерпретации данных. Тем самым работа компьютеров допускает строгую однозначную проверку правильности своей работы в плане заложенных в них процедур и алгоритмов обработки информации. Это позволяет использовать математический аппарат для анализа и разработки логических устройств вычислительной техники.Функцией логических переменных называют взаимосвязь логических переменных по законам логики. Значения входных переменных и выходных функций связаны некоторым преобразованием, которое реализует логическую функцию.Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность (таблица №1).В алгебре логики любую логическую функцию можно выразить через основные логические операции, записать ее в виде логического выражения и упростить ее, применяя законы логики и свойства логических операций. По формуле логической функции легко рассчитать ее таблицу истинности. Необходимо только учитывать порядок выполнения логических операций (приоритет) и скобки. Операции в логическом выражении выполняются слева направо с учетом скобок. 

---

Приоритет выполнения логических операций: 1. Действие в скобках; 2. Действие под отрицанием; 3. Инверсия; 4. Конъюнкция; 5. дизъюнкция.Таблица №1

Логическая операция	Название	Соответствует союзу	Обозначение знаками	Таблица истинности	Логическая операция
Инверсия (от лат. inversion – переворачиваю)	отрицание	не А		А 1 0 0 1	Опр. 8 Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Конъюнкция (от лат. conjunction – связываю)	Логическое умножение	А и В		А В 1 1 1 1 0 0 0 1 0 0 0 0	Опр.9Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны.
Дизъюнкция (от лат. disjunction – различаю)	Логическое сложение	А или В		А В 1 1 1 1 0 1 0 1 1 0 0 0	Опр. 10 Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.
Импликация (от лат. implication – тесно связывать)	Логическое следование	Если А, то В; Когда А, тогда В	А–условие В-следствие	А В 1 1 1 1 0 0 0 1 0 0 0 1	Опр. 11 Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие.
Эквивалентность (от лат. equivalents - равноценность)	Логическое равенство	А тогда и только тогда, когда В		А В 1 1 1 1 0 0 0 1 0 0 0 1	Опр. 12 Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны

---

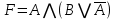
Пример1.Построить таблицу истинности для логической функции Решение:

1. 
   Определить количество строк в таблице истинности, которое равно  количеству возможных комбинаций значений логических переменных, входящих в логическое выражение: количество строк равно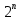 , где n – количество переменных
   

Количество логических переменных – 2 (A, B) поэтому количество строк – 2ⁿ = 4

A	B
0	0
0	1
1	0
1	1

2. 
   Определить количество столбцов:
   

количество столбцов=количество переменных + количество операций, используя приоритет операций.Количество логических операций -3 (умножение – 1, сложение – 1, отрицание – 1), поэтому количество столбцов 2+3=5

3. 
   Построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных и заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности:
   

A	B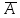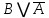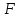
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	1	0	1	1

Арифметико-логические основы работы компьютера

---

Все логические схемы ЭВМ строятся на логических элементах, реализующих логические функции. Под логическим элементом понимают техническое устройство, реализующее одну элементарную булеву функцию. Обычно для построения схем используются логические элементы, реализующие основные логические функции И, ИЛИ, НЕ: конъюнктор (схема И); дизъюнктор (схема ИЛИ), инвертор (схема НЕ). Стандартные обозначения этих элементов выглядят следующим образом:элементых & 1₁ х₁ у=х₁х₂ у=х₁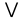 х₂ х у=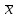х₂ х_{2 конъюнктор дизъюнктор инвертор}Конструктивно логические объединяются в единые корпуса – интегральные микросхемы (ИМС). В одном корпусе ИМС могут быть один, две и более логических элементов. Схемы И, ИЛИ, НЕ образуют базис, то есть с их помощью можно реализовать любую булеву функцию на основе суперпозиции. Применяемые на практике комплексы ИМС имеют в своём составе такие логические элементы, как И-НЕ, ИЛИ-НЕ, которые образуют универсальный базис. 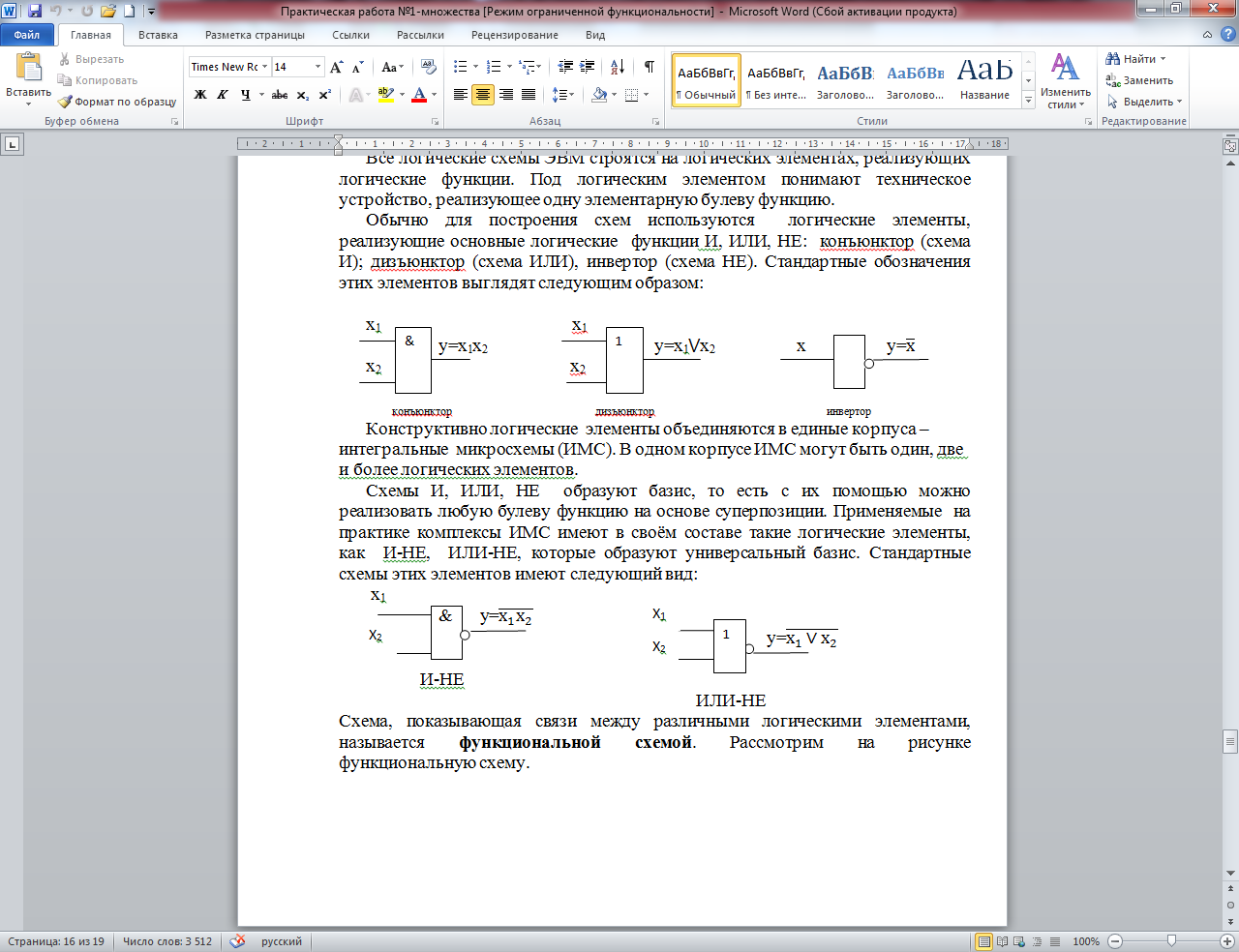Стандартные схемы этих элементов имеют следующий вид:Схема, показывающая связи между различными логическими элементами, называется функциональной схемой. Рассмотрим на рисунке функциональную схему.
Х₁

---

Х₂
у & & & 1
t₁

t₂

t₃
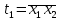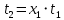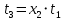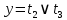
Существуют разные задачи работы с функциональными схемами.Задача1.Найти по функциональной схеме логическую функцию, описывающую работу этой схемы с помощью аппарата алгебры логики. В качестве примера построим логическую функцию, представленной на рисунке выше. Для этого каждому логическому элементу схемы поставим в соответствие логический оператор: ; ; ; Этим установлено однозначное соответствие между элементами схемы и её математическим описанием. 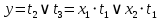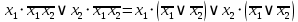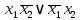Затем выполним последовательно операции подстановки и преобразования до тех пор, пока не получится функция, выраженная через входные переменные: = = Задача 2. Построить функциональную схему по логической функции 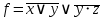. Затем построить схему, используя как базисные, так и дополнительные вентили, следуя по приоритету операций.Построим схему: 1 y х z f 1 &Вопросы для размышления1. Для чего нужно изучать функциональные схемы в информатике?

---

Смотрите также файлы

• Блім бойынша жиынты баалау мен тосанды жиынты баалау нтижелері бойынша талдау іv тосан аза тілі.docx

• 10 СЖ тапсырмалары.docx

• Курсовой проект по дисциплине Сетевые технологии На тему Проектирование локальной вычислительной сети предприятия.doc

• авимед кпсалалы колледжі Техникалы жне ксіптік білім беру Мамандыы 09160100 Фармация.docx

• Опишите дальнейшую работу с нормативным актом и какие последствия ожидают данный нормативный акт.docx