Файл: Теоретические аспекты изучения методики решения текстовых задач в основной школе Сущность понятия текстовая задача. Роль текстовых задач в обучении математике.docx

Задачи, в которых все объекты математические (вычислительные задания, доказательство теорем и т.д.) принято называть математическими задачами. Математические задачи называются текстовыми, если в них присутствует хотя бы один объект, который является реальным предметом.

Важнейшая особенность текстовых задач заключается в том, что  в них не показывается, открыто, какое собственно действие необходимо выполнить для получения ответа на вопрос задачи. В любой текстовой задаче можно выделить следующее: числовые значения, которые принято называть известными или данными (их следует быть не менее двух); некоторую систему функциональных зависимостей в неявном виде, взаимоотношения данных и искомых и данных между собой; вопрос или требование, на который нужно найти ответ.

Условие задачи называют числовые значения величин и имеющиеся между ними некие связи, то есть качественные и количественные характеристики предметов задачи и взаимоотношений между ними. В задаче, как правило, не одно условие, а несколько, которые называют элементарными. Вопрос в задаче может быть выражен как в повествовательной, так и в вопросительной форме, и их также как условий, может быть несколько. Значение величин, которые необходимо найти называют искомой величиной, а числовые величины искомых значений, называют неизвестными или искомыми.

Для того чтобы получить ответ на требование задачи, для этого необходимо ее решить. Решить задачу это значить найти взаимоотношения между данными, которые даны в условии задачи, и искомыми величинами, установить последовательность применение общих положений математики (формул, законов, правил, и так далее), выполнить определенные действия которые даны в задаче, применяя общее положение и получить ответ на требование задачи или доказать что его нет.

Стандартные задачи - математические задачи, для решения которых имеются готовые правила в курсе математики .

Процесс решения стандартных задач имеет следующие особенности:

1) установление (распознавание) вида задач;

2) поиск решения, в том числе составление на основе общего правила (формулы, тождества) или общего положения (определения, теоремы) алгоритма;

3) решение стандартной задачи.

Отсюда следует следующее, чтoбы легко решать стандартные задачи (а они являются основными математическими задачами, ибо все другие в конечном итоге сводятся к ним), нужно:

1) помнить все изученные в курсе математики общие правила (формулы, тождества) и общие положения (определения и теоремы).

---

2) уметь развертывать свернутые общие правила, формулы, тождества, а также определения и теоремы в программы - последовательности шагов решения задач соответствующих видов.

- задачи, для которых в курсе математики нет общих правил и положений, которые определяют точный алгоритм их решения.

Рассмотрим пример таких задач.

Пример. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 ч 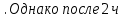пути они уменьшили скорость на 0,5 км/ ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?

Для подобных задач никакого общего правила, определяющего точную программу их решения, не существует. Однако это не значит, что вообще нет каких-то общих подходов к решению таких задач.

Сначала определяем вид задачи и, исходя из этого, возникает идея решения («составить уравнение»). Для этого, пользуясь весьма общими указаниями и образцами решения подобных задач, составляется уравнение.

Полученное уравнение представляет собой уже стандартную задачу. Решив ее, тем самым, решили и исходную нестандартную задачу. Процесс решения любой нестандартной задачи состоит в последовательном применении двух основных операций:

- сведение (путем преобразования или переформулирования) нестандартной задачи к другой, ей эквивалентной, но уже стандартной задаче;

- разбиение нестандартной задачи на несколько стандартных подзадач.

Общих правил для решения нестандартных задач нет. В отличие от математических правил эвристики носят характер необязательных рекомендаций, советов, следование которым может привести (а может и не привести) к решению задачи.

По характеру требования Л.М. Фридман и Е.Н. Турецкий все задачи делят на три основных класса:

1. Задачи на нахождение Примеры таких задач - задачи на вычисление разных выражений, значений функций, задачи на установление характера функции и пр. Этот класс задач многочисленный и разнообразный.

2. Задачи на доказательство или объяснение. Все задачи, требование которых начинается со слов «доказать», «проверить» или содержащие вопрос «Почему?», относятся к этому классу задач .

3. Задачи на преобразование или построение. К этому классу относятся задaчи, в которых требуется преобразовать какое-либо выражение.

---

Т.Е. Демидова и А.П. Тонких предлагают классифицировать задачи по их типу и виду, понимая под типом задачи классификацию по содержанию: задачи на движение, задачи на части, задачи на проценты и т.п.

Под решением задачи понимает воздействие на предмет задачи, обусловливающее ее переход из исходного состояния в требуемое. Решенная задача, т. е. задача, предмет которой приведен в требуемое состояние, перестает быть задачей .

Далее рассмотрим этапы процесса решения задачи.

1) Анализ задачи - первый этап. Ключевое назначение этапа – осмыслить ситуацию, которая представлена в задаче; выявить условия и требования, отношения между объектами задачи.

Анализ задачи возможно осуществлять по двум направлениям:

- предметно-содержательный анализ – декодирование условия задачи в целом, воссоздание реальной задачной ситуации, модель которой - данная задача. Такой анализ обычно проводят устно;

- логико-семантический анализ – анализ текста задачи для установки величин, значений, соотношений между ними. Таким образом, выявляется структура задачи.

На этом этапе решения задачи можно использовать такие приемы:

- представление жизненной ситуации, которая описана в задаче – выполняется при чтении или слушании задачи.

- постановка специальных вопросов;

- перефразировка текста, состоящая в замене описания некоторой ситуации другим.

2) Оформление анализа посредством составления схематической записи, т.е. вспомогательной модели, помогающей перевести текст задачи со словесного языка в математический.

Схематическая запись может быть представлена в виде: схемы, таблицы, чертежа, рисунка, ключевых слов.

Чертежи должны быть наглядно представлены, четкие, соответствовать тексту задачи; на них должны быть отражены по возможности все данные, входящие в условие задачи. После построения вспомогательной модели необходимо проверить:

- все ли объекты задачи показаны на модели;

- все ли отношения между объектами отражены;

- все ли числовые данные приведены;

- есть ли требование.

3) Поиск способа решения данной задачи. Назначение этапа – завершить установление связей между данными и искомыми величинами и указать последовательность использования этих связей (составить план решения).

Поиск пути решения можно осуществлять от вопроса задачи к данным – аналитический путь, или от данных к вопросу – синтетический путь. Анализ в форме рассуждения от искомого к данным подразделяется на два вида: восходящий и нисходящий.

---

Общая схема восходящего анализа заключается в следующем: пусть требуется доказать утверждение А. Подбираем такое утверждение В, из которого следует А. Затем отыскиваем утверждение С, из которого следует В, и т. д. до тех пор, пока находим путь решения задачи.

Особенности данного метода:

1) при восходящем анализе не требуется обратимости рассуждений;

2) применяя восходящий анализ, фактически пользуемся аналитико-синтетическим методом;

3) общая схема восходящего анализа несколько отличается от формы, словесных рассуждений при его использовании;

4) в общей схеме восходящего анализа (в отличие от нисходящего) не разъясняется, получить утверждение, из которого следует искомое. Такое утверждение подыскивается, исходя из конкретных условий решаемой задачи.

В.А. Далингер предлагает разбор задачи от ее вопроса к ее условию изобразить в виде схемы – «дерево рассуждений». Построение этого «дерева» называется анализом, а решение задачи по данной схеме – синтезом.

4) Когда способ решения задачи найден, его нужно осуществить. Назначение этапа – найти ответ на требование задачи, выполнив все действия в соответствии с планом. Немаловажную роль играет запись решения.

5) После того как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи.

Проверка решения текстовых задач может быть прямой или косвенной, в свою очередь, каждая из них может быть полной или неполной (частичной).

Прямая полная проверка решения состоит в том, что убеждаемся в выполнении всех условий задачи при найденных значениях искомых.

Неполная проверка состоит в том, что мы проверяем выполнение не всех условий, а лишь некоторых.

Косвенную проверку задачи можно произвести с помощью составления и решения обратной задачи. Обратная задача составляется путем обмена ролями одного из искомых с каким-либо из данных.

6) При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и притом, сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т. д. Все это составляет шестой этап процесса решения.

---

7) Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо четко сформулировать ответ задачи, - это будет седьмой этап процесса решения.

8) Анализ выполненного решения.

Из указанных восьми этапов пять являются обязательными, и они имеются (в том или ином виде) в процессе решения любой задачи. Это этапы анализа задачи, поиска способа ее решения, осуществления решения, проверки решения и формулирования ответа. Остальные три этапа (схематическая запись задачи, исследование задачи и заключительный анализ решения) являются не обязательными и в процессе решения многих задач не используются.

Итак, рассмотрены основные способы классификации задач, их содержание. Педагогу необходимо оперировать всеми способами и а также объяснять решения задач для учащихся, осуществлять индивидуальный подход к ученикам.

3. Методы и приемы решения текстовых задач в основной школе

Существуют различные методы решения текстовых задач, основными из которых являются: арифметический, алгебраический, геометрический, логический, практический и др. В основе каждого метода лежат различные виды математических моделей.

Однако, прежде чем, перейти к рассмотрению методов решения текстовых задач, определим понятие «решить задачу».

Решить задачу – означает найти все ее решения или доказать, что их нет.

Охарактеризуем первые три метода решения текстовых задач, являющихся наиболее распространенными в школьном курсе математики.

1. 
   Арифметический метод. Решить задачу арифметическим методом – значит найти ответ на условие задачи через выполнение арифметических действий над числами. Часто решить задачу можно различными алгебраическими способами, т.е. одна и та же задача может решаться посредством различных арифметических действий.
   
2. 
   Алгебраический метод. Данный метод представляет собой метод буквенных вычислений. Решить задачу алгебраическим методом – значит отыскать ответ на условие задачи путем составления и решения уравнения или системы уравнений (или неравенств).
   
3. 
   Геометрический метод. Состоит в том, что решение задачи или доказательство сопровождается наглядным представлением. Иногда решение или доказательство видно из рисунка к задаче. В дальнейшем под геометрическим методом решения текстовых задач будем понимать такой метод решения, который заключается в использовании геометрических представлений, законов геометрии и элементов аналитических методов (уравнений (неравенств), систем уравнений, арифметических выражений и др.).
   

---