Файл: Теоретические аспекты изучения методики решения текстовых задач в основной школе Сущность понятия текстовая задача. Роль текстовых задач в обучении математике.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 129
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Используя конструктивный прием, все построения выполняются на миллиметровой бумаге в клетку, применяя масштаб. Даже с учетом того, что ответ задачи получается приближенный, однако он является допустимым для практических целей, и находится посредством измерений длин отрезков или иных элементов чертежа.
Конструктивно-аналитический прием позволяет выполнить чертеж схематически, от руки. Таким образом, для решения алгебраической задачи геометрическим методом необходимо:
-
построить геометрическую модель задачи: решающую или вспомогательную (геометрическая модель задачи называется решающей, если она позволяет получить ответ задачи без аналитических выкладок, в противном случае – вспомогательной). -
найти ответ задачи: если модель решающая, то ответ «снимаем» с чертежа, в случае вспомогательной геометрической модели надо:
а) составить числовое выражение или уравнение (систему уравнений), неравенство (систему неравенств), используя геометрические соотношения полученных фигур;
б) найти значение числового выражения или уравнения, неравенства (системы уравнений или неравенств);
в) исследовать полученные решения.
Так, для того, чтобы решить текстовую задачу с помощью графиков линейной функции, надо:
1. Задать систему координат sOt с осью абсцисс Ot и осью ординат Os. Для этого по условию задачи надо выбрать начало отсчета: начало движения объекта или из нескольких объектов избирается тот, который начал двигаться раньше или прошел большее расстояние. По оси абсцисс отметить интервалы времени в его единицах измерения, а по оси ординат отметить расстояние в выбранном масштабе его единиц измерения.
2. Провести линии движения каждого из объектов, указанных в условии задачи, через координаты хотя бы двух точек прямых. Обычно скорость объекта даёт информацию о прохождении расстояния за одну единицу времени от начала его движения. Если объект начинает двигаться позже, то точка начала его движения смещена на заданное число единиц вправо от начала отсчета вдоль оси абсцисс. Если объект начинает двигаться с места, удаленного от начала отсчета на определённое расстояние, то точка начала его движения смещена вверх вдоль оси ординат.
3. Место встречи нескольких объектов на координатной плоскости обозначено точкой пересечения прямых, изображающих их движение, значит, координаты этой точки дают информацию о времени встречи и удаленности места встречи от начала отсчета.
4. Разность скоростей движения двух объектов определяется длиной отрезка, состоящего из всех точек с абсциссой 1, расположенных между линиями движения этих объектов.
5. Точки на координатной плоскости должны быть отмечены в соответствии с масштабом по условию задачи, и линии должны быть построены аккуратно. От этого зависит точность решения задачи. Иногда полезно за единичный отрезок на оси абсцисс брать количество клеток, кратное условиям задачи относительно времени, а на оси ординат – количество клеток, кратное условиям задачи относительно расстояния. Например, 12мин по времени требуют выбора числа клеток кратное 5, т.к. 12 мин составляет пятую часть часа.
6. Решение задач графическим методом требует творческого подхода и глубокого понимания процессов, описанных в задаче. Изображая графики процессов, можно находить зависимости между величинами, применяя геометрические знания, а можно решать задачу привычным способом.
Задача учителя математики − научить школьника представлять конкретные объекты в форме символической модели, чтобы помочь ему выработать навыки перевода текстовой задачи на математический язык.
Приведем пример решения задачи геометрическим методом.
Задача 1. От посёлка до станции велосипедист ехал со скоростью 10км/ч, а возвращался со скоростью 15км/ч, поэтому он затратил на обратный путь на 1ч меньше. Найдите расстояние от посёлка до станции.
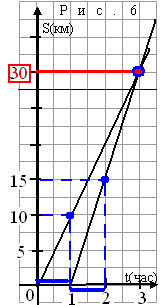
Рис. 2. Рисунок к задаче 1
Решение:
1. Зададим координатную плоскость sOt c осью абсцисс Оt, на которой отметим интервалы времени движения, и осью ординат Os, на которой отметим расстояние от посёлка до велосипедиста (Рис. 1).
2. Нанесём деления в масштабе: по оси ординат – в двух клетках 5км; по оси абсцисс – один час в 2 клетках (в 1 клетке – 30 мин).
3. Построим линию движения Iтуда: начало движения отметим точкой (0;0). Велосипедист ехал со скоростью 10км/ч, значит, прямая должна пройти через точку (1;10).
4. Построим линию движенияIIобратно: конец линии отметим точкой (1;0), т.к. велосипедист затратил на обратный путь на 1час меньше и вернулся в посёлок. Он ехал со скоростью 15км/ч, значит следующая точка прямой имеет координату.
5. Отметим Α(3; 30) - точку пересечения прямыхI и II: её ордината покажет расстояние от посёлка до станции: s = 30. Откуда следует, что расстояние от посёлка до станции 30 км.
Таким образом, в соответствии с современной терминологией текстовая проблема является вербальной моделью ситуации, явления, события, процесса и т. д. Как и в любой модели, текстовая проблема не описывает все событие или явления, а только ее количественные и функциональные характеристики.
Основные методы решения текстовых задач являются арифметическими и алгебраическими. Кроме того, для решения текстовых задач используются логические, практические и комбинированные методы.
Существуют различные типы текстовых задач. Способность различать их помогает правильно ориентироваться в выборе более эффективного способа ее решения. Наиболее распространенными являются:
- задачи на движение (встречный трафик, движение в одном направлении, движение по реке и т. д.);
- задачи на работу;
- задачи на смеси, сплавы, концентрации;
- задачи на интерес.
Рассмотрим классификацию текстовых задач и способы их решения :
- арифметический метод (решение текстовой задачи с помощью чисел и признаков арифметических операций сложения, вычитания, умножения и деления, т. е. с помощью нескольких действий по числам, связанным друг с другом);
- алгебраический метод (решение путем введения переменных и составления соответствующего уравнения или неравенства или системы уравнений или неравенств);
- геометрический метод (решение проблемы путем построения геометрических форм и использования их свойств);
- графический метод (решение текстовой задачи с использованием графиков в прямоугольной системе координат);
- схематический способ (решение задачи с помощью схем).
Эта классификация довольно условна, т.к. одна и та же задача может быть решена по-разному.
В процессе решения задач обучающиеся приобретают новые математические знания, готовятся к практической деятельности.
Таким образом, важно, чтобы учитель математики, понимая роль задачи и ее место в воспитании обучающегося, разумно подходил к выбору задачи и методов ее решения, помнил, что он должен научить школьника решать задачи различными способами, подбирая наиболее эффективные из них. Решение задач позволяет сформировать у учащихся практические навыки, которые пригодятся им в повседневной жизни.
1. Балл Г.А. Теория учебных задач. – М.: Педагогика, 1990.
29. Фридман Л.М. Как научиться решать задачи: Кн. для учащихся ст. классов сред. шк. / Л.М. Фридман, Е.Н. Турецкий – 3-е изд., дораб. – М.: Просвещение, 1989. – 192 с.: ил.
30. Фридман Л.М. Логико-психологический анализ учебных задач. - М.: Педагогика, 1977. – С. 67 – 161.
31. Фридман Л.М. Сюжетные задачи по математике. История, теория, методика. – М.: Школа-пресс, 2002.